2022年中考数学二轮专题复习-一次方程、不等式

试卷更新日期：2022-03-30 类型：二轮复习

进入出卷网下载

一、单选题

1. 如果 $x = 1$ 是关于 $x$ 的方程 $3 x + 2 m = 9$ 的解，则 $m$ 的值为（）

A、 $\frac{1}{3}$ B、1 C、3 D、6

查看试题解析
2. 已知 $(k - 1) x^{k^{2}} + 3 = 0$ 是关于x的一元一次方程，则 $k$ 的值是（）

A、-1 B、1 C、-1或1 D、0

查看试题解析
3. 将梯形面积公式 $S = \frac{1}{2} (a + b) h$ 变形成已知S，a， $b$ ，求 $h$ 的形式，则 $h =$ （）

A、 $\frac{1}{2} (a + b) S$ B、 $\frac{2 S}{a + b}$ C、 $\frac{S}{2 a + 2 b}$ D、 $2 S - a - b$

查看试题解析
4. 如图是一种正方形地砖的花型设计图，为了求这个正方形地砖的边长，可根据图示列方程（）

A、 $4 - 2 x = 6 x$ B、 $2 + 4 x = 6 x$ C、 $2 + 6 x = 4 x$ D、 $4 + 2 x = 6 x$

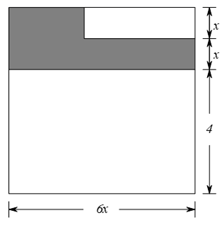查看试题解析
5. 已知x＞y，则下列不等式不成立的是（）

A、﹣3x+6＞﹣3y+6 B、2x＞2y C、﹣3x＜﹣3y D、x﹣6＞y﹣6

查看试题解析
6. 若实数 $a$ 既使得关于 $x$ 的不等式组 ${\begin{matrix} \frac{x}{2} + 1 \leq \frac{x + 4}{3} \\ x + 1 > \frac{a + x}{2} \end{matrix}$ 有解，又使得关于 $y$ 的分式方程 $\frac{3 - a y}{3 - y} - 1 = \frac{3}{y - 3}$ 有整数解，则满足条件的所有整数 $a$ 的和为（）

A、4 B、2 C、0 D、-2

查看试题解析
7. 甲、乙两队开展足球对抗赛，规定每队胜-场得3分，平-场得1分，负一场得0分甲队与乙队一共比赛了10场，甲队保持了不败记录，一共得了22分，设甲队胜了x场，则列方程为（）

A、x-3（10-x） =22 B、3x-（10-x） =22 C、x+3（10-x） =22 D、3x +（10-x） =22

查看试题解析
8. 关于x的不等式组 ${\begin{array}{l} \frac{x - 1}{2} - \frac{x + 2}{3} ⩽ 1 \\ x - a > 2 \end{array}$ 只有3个整数解，求a的取值范围（）

A、8＜a＜9 B、8≤a≤9 C、8≤a＜9 D、8＜a≤9

查看试题解析
9. 某项工程，甲单独完成需要45天，乙单独完成需要30天，若乙先单独做22天，剩下的由甲去完成，问：甲、乙一共用几天可完成全部工作？设甲、乙共用x天完成，则符合题意的方程是（）

A、 $\frac{x - 22}{45} + \frac{22}{30} = 1$ B、 $\frac{x + 22}{30} + \frac{x}{45} = 1$ C、 $\frac{x + 22}{45} + \frac{22}{30} = 1$ D、 $\frac{x}{30} + \frac{x - 22}{45} = 1$

查看试题解析
10. 两位同学在解同一个方程组时，甲同学由 ${\begin{array}{l} a x + b y = 9 ， \\ x + c y = 11 \end{array}$ 正确地解出 ${\begin{array}{l} x = 5 ， \\ y = 3 ， \end{array}$ 乙同学因看错了 $c$ 而解得 ${\begin{array}{l} x = - 1 ， \\ y = - 6 \end{array}$ 那么a，b，c的正确的值为（）

A、 $a = 3 ， b = - 2 ， c = 2$ B、 $a = 1 ， b = \frac{4}{3} ， c = 2$ C、 $a = 3 ， b = - 2 ， c = - 2$ D、 $a = 1 ， b = \frac{4}{3} ， c = - 2$

查看试题解析
11. 已知 $△ A B C$ 的三边分别为a、b、c，且 $\sqrt{a - 5} + {(b - 12)}^{2} + | c - 13 | = 0$ ，则 $△ A B C$ 的面积为（）

A、30 B、60 C、65 D、无法计算

查看试题解析
12. 已知▱ABCD的周长为34cm，两邻边之差3cm，则两邻边长分别为（）

A、10cm，7cm B、11cm，6cm C、12cm，5cm D、18.5cm，15.5cm

查看试题解析
13. 轮船从甲地顺流开往乙地，所用时间比乙地逆流回到甲地少 $1.5$ 小时，已知轮船在静水中速度为每小时20千米，水流速度为每小时3千米，求甲乙两地距离．若设两地距离为 $x$ 千米，则可得方程（）．

A、 $\frac{x}{20} - \frac{x}{20 - 3} = 1.5$ B、 $\frac{x}{20 + 3} - \frac{x}{20 - 3} = 1.5$ C、 $\frac{x}{20 - 3} - \frac{x}{20} = 1.5$ D、 $\frac{x}{20 - 3} - \frac{x}{20 + 3} = 1.5$

查看试题解析
14. 如图，小明将一张正方形纸片剪去一个宽为3cm的小长方形后，再从剩下的长方形纸片上剪去一个宽为4cm的小长方形、若两次剪下的小长方形的面积正好相等，则最终剩余长方形纸片（阴影部分）的面积为（）

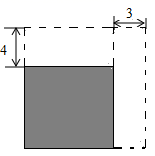A、64cm² B、72cm² C、81cm² D、90cm²

查看试题解析
15. 若关于x的不等式mx﹣n＞0的解集是x＜ $\frac{1}{5}$ ，则关于x的不等式（m+n）x＞n﹣m的解集是（　　）

A、x＜﹣ $\frac{2}{3}$ B、x＞﹣ $\frac{2}{3}$ C、x＜ $\frac{2}{3}$ D、x＞ $\frac{2}{3}$

查看试题解析
16. 如图，在长方形ABCD中，AB＝4cm，BC＝3cm，E为CD的中点，动点P从A点出发，以每秒1cm的速度沿A→B→C→E运动，最终到达点E．若点P运动的时间为x秒，则当△APE的面积为5cm²时，x的值为（）

A、5 B、3或5 C、 $\frac{10}{3}$ D、 $\frac{10}{3}$ 或5

查看试题解析
17. 规定： $f (x) = | x + 2 |$ ， $g (x) = | x - 4 |$ ，例如 $f (- 4) = | - 4 + 2 | = 2$ ， $g (- 4) = | - 4 - 4 | = 8$ ，下列结论中，
（1）能使 $f (x) = 5$ 成立的x的值为3或-7；（2）若x<-2，则 $f (x) + g (x) = 2 - 2 x$ ；（3）若 $f (x) + g (y) = 0$ ，则2x-3y=-16；（4）式子 $f (x - 1) + g (x + 1)$ 的最小值是4.正确的是（）

A、（1）（2）（3） B、（1）（2）（4） C、（1）（3）（4） D、（1）（2）（3）（4）

查看试题解析
18. 某种出租车的收费标准是：起步价7元(即行驶距离不超过3千米都收7元车费)，超过3千米以后，超过部分每增加1千米，加收2.4元(不足1千米按1千米计)．某人乘这种出租车从甲地到乙地共支付19元，设此人从甲地到乙地经过的路程是x千米，那么x的取值范围是（）

A、1＜x≤11 B、7＜x≤8 C、8＜x≤9 D、7＜x＜8

查看试题解析
19. 若 $a$ ， $b$ ， $c$ 是 $Δ A B C$ 的三边长，且 $a^{2} + b^{2} + c^{2} - a b - a c - b c = 0$ ，则 $Δ A B C$ 的形状是（）

A、等腰三角形 B、等腰直角三角形 C、等边三角形 D、不能确定

查看试题解析
20. 我们规定： $[m]$ 表示不超过 $m$ 的最大整数，例如： $[3.1] = 3$ ， $[0] = 0$ ， $[- 3.1] = - 4$ ，则关于 $x$ 和 $y$ 的二元一次方程组 ${\begin{array}{l} [x] + y = 3.2 \\ x - [y] = [3.2] \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ y = 0.2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1.2 \end{array}$ C、 ${\begin{array}{l} x = 3.3 \\ y = 0.2 \end{array}$ D、 ${\begin{array}{l} x = 3.4 \\ y = 0.2 \end{array}$

查看试题解析

二、填空题

21. 已知x＝3是关于x的方程ax+2x﹣9＝0的解，则a的值为．

查看试题解析
22. 不等式 $2 x - 1 > \frac{1}{2} x$ 的解集是.

查看试题解析
23. 不等式组 ${\begin{array}{l} 5 x + 4 > 3 x \\ \frac{x - 1}{2} \leq \frac{2 x - 1}{5} \end{array}$ 的解是.

查看试题解析
24. 若 $| a + 3 | + {(b - 2)}^{2} = 0$ ，则 $a^{b}$ = ．

查看试题解析
25. 若（2x﹣y）²与|x+2y﹣5|互为相反数，则（x﹣y）²⁰²²＝.

查看试题解析
26. 如图，一个桌球游戏的长方形桌面ABCD中，AD=2m，现将球从AB边上的点M处发射，依次与边AD，DC，CB触碰并反弹后第一次回到AB边上的点N处，设触碰点依次为E，F，G，当AE=AM，DE=DF，CF=CG，BG=BN，MN=0.6m时，AB的长为m．

查看试题解析
27. 不等式 $\frac{1}{2} x - 3 > - 14 - \frac{5}{2} x$ 的最小负整数解.

查看试题解析
28. 若方程组 ${\begin{array}{l} 2 a - 3 b = 13 \\ 3 a + 5 b = 30 \end{array}$ 的解是 ${\begin{array}{l} a = 8.3 \\ b = 1.2 \end{array}$ ，则方程组 ${\begin{array}{l} 2 (x + 2) - 3 (y - 1) = 13 \\ 3 (x + 2) + 5 (y - 1) = 30 \end{array}$ 的解是．

查看试题解析
29. 已知，数轴上A，B，C三点对应的有理数分别为a，b，c．其中点A在点B左侧，A，B两点间的距离为2，且a，b，c满足 $| a + b | + (c - 2022)^{2} = 0$ ，则a＝．对数轴上任意一点P，点P对应数x，若存在x使 $| x - a | + | x - b | + | x - c |$ 的值最小，则x的值为．

查看试题解析
30. 如图， $A B = 20 cm$ ，点 $C$ 是线段 $A B$ 的中点，点 $P$ 从点 $A$ 出发，以 $2 cm/s$ 的速度向右移动，同时点 $Q$ 从点 $C$ 出发，以 $3cm/s$ 的速度向右移动到点 $B$ 后立即原速返回点 $A$ ，当点 $Q$ 到达点 $A$ 时， $P 、 Q$ 两点同时停止运动.当 $P Q = 12 cm$ 时，运动时间 $t$ 的值是.

查看试题解析

三、计算题

31. 解下列方程：

(1)、 $- 3 x = 15$ ；

(2)、 $- \frac{n}{3} - 2 = 10$ ．

(3)、 $0.7 x - 0.8 = 6.7 - 1.8 x$ ．

(4)、 $\frac{1 - 2 x}{5} = \frac{3 x + 2}{7} - 4$ ．

查看试题解析
32. 解不等式（组）

(1)、 $2 (x + 1) - 1 > x$

(2)、 ${\begin{cases} - x + 1>3 \\ \frac{2 x - 1}{2} \leq \frac{x + 2}{3} + 1 \end{cases}$

查看试题解析
33. 解方程组：

(1)、 ${\begin{array}{l} x - 2 y = - 2 \\ 2 x - y = 2 \end{array}$

(2)、 ${\begin{array}{l} 4 (x - y - 1) = 3 (1 - y) - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{array}$

查看试题解析
34. 解下列方程组

(1)、 ${\begin{matrix} x - 2 y = 1 ① \\ 4 x + 3 y = 26 ② \end{matrix}$ . （代入消元法）

(2)、 ${\begin{array}{l} 2 x + 3 y = 3 ① \\ 5 x - 3 y = 18 ② \end{array}$ （加减消元法）

查看试题解析

四、解答题

35. 解不等式组 ${\begin{matrix} 4 x - 2 \geq 3 (x - 1) \\ \frac{x - 5}{2} + 1 > x - 3 \end{matrix}$ ，并把解集在数轴上表示出来

查看试题解析
36. 小李在解方程 $\frac{3 x + 5}{2} - \frac{2 x - m}{3} = 1$ 去分母时方程右边的1没有乘以6，因而得到方程的解为x=﹣4，求出m的值并符合题意解出方程．

查看试题解析
37. 已知 $y = a x^{2} + b x + c$ ，当 $x = 1$ 时， $y = 5$ ；当 $x = - 2$ 时， $y = 14$ ；当 $x = - 3$ 时， $y = 25$ .求a，b，c的值.

查看试题解析
38. 一些相同的房间需要粉刷墙面．一天3名一级技工去粉刷8个房间，结果其中有50m²墙面未来得及粉刷；同样时间内5名二级技工粉刷了10个房间之外，还多粉刷了另外的40m²墙面，已知每名同级别的技工每天的工作效率相同，每名一级技工比二级技工一天多粉刷10m²墙面．求每个一级技工和二级技工每天粉刷的墙面各是多少平方米？

查看试题解析
39. 为了响应国家“节能减排，绿色出行”号召，昌平区多个地点安放了共享单车，供行人使用．已知甲站点安放共享单车79辆，乙站点安放共享单车50辆．通过调查发现，甲站点人流量较大，共享单车的需求量较高，因此要对两个站点的共享单车数量进行调整．为了使甲站点的共享单车数量是乙站点的2倍，需要从乙站点调配多少辆共享单车到甲站点?

查看试题解析
40. 如图，已知点A、点B在数轴上表示的数分别是-20、64，动点M从点A出发，以每秒若干个单位长度的速度向右匀速运动，动点N从点B出发，以每秒若干个单位长度的速度向左匀速运动．若点M、N同时出发，则出发后12秒相遇；若点N先出发7秒，则点M出发10秒后与点N相遇．动点M、N运动的速度分别是多少？

查看试题解析

41. 为鼓励居民节约用电，某省试行阶段电价收费制，具体执行方案如表：

档次	每户每月用电量（度）	执行电价（元/度）
第一档	小于等于200	0.55
第二档	大于200小于400	0.6
第三档	大于等于400	0.85

某户居民五、六月份共用电500度，缴电费290.5元.已知该用户六月份用电量大于五月份，且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度？

查看试题解析

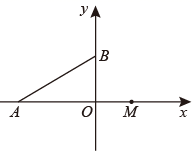
42. 如图，在平面直角坐标系中，已知点A(a，0) $B (0 ， b)$ ，．
（Ⅰ）如图，若 $| a + b + 1 | + \sqrt{3 a + 4 b} = 0$ ，已知点 $C (m ， - m)$ ．

①连接AC ，当 $A C // y$ 轴时，求m的值：

②若 $△ A B C$ 的面积是8，求m的值：

（Ⅱ）如图，若 $∠ A B O = 60 °$ ，射线BA以每秒9°的速度绕点B顺时针方向旋转至射线BA₁ ，点M为x轴正半轴上一点，射线MO以每秒6°的速度绕点M逆时针方向旋转到MO₁ ，设运动时间为t秒 $(0 < t < 30)$ ，求t为多少秒时，直线 $B A_{1} // M O_{1}$ ？

查看试题解析

五、综合题

43. 平面直角坐标系中，点A(x，y)，且x²－8x＋16＋＝0，△ABC是以AB为斜边的等腰直角三角形(点A、B、C逆时针排列).

(1)、直接写出点A的坐标是；

(2)、如图1，已知点B(0，n)且0＜n＜4，连接OC. 求四边形ABOC的面积；

(3)、如图2，已知点B(m，n)且0＜m＜4，0＜n＜4，过点A作AD⊥y轴于D，连接OB，M为OB的中点，连接DM、CM. 求证：DM⊥CM.

查看试题解析