浙江省庆元二中2021-2022学年八年级下学期3月质量检测数学试卷

试卷更新日期：2022-03-30 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30分）

1. 下列二次根式中是最简二次根式的是（）

A、 $\sqrt{0.3}$ B、 $\sqrt{8}$ C、 $\sqrt{14}$ D、 $\sqrt{1 \frac{1}{2}}$

查看试题解析
2. 下列是一元二次方程的是（）

A、x²-2x-3=0 B、2x+y= 5 C、 $\frac{x}{2} + \frac{1}{x}$ =1 D、x+1=0

查看试题解析
3. 关于×的方程 3x²-2= 4x中，二次项系数和一次项系数分别是（）

A、3，-2 B、3，4 C、3，-4 D、-4，-2

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{{(- 5)}^{2}}$ =±5 B、3 $\sqrt{5}$ - $\sqrt{5}$ =2 $\sqrt{5}$ C、（- $\sqrt{5}$ ）² =-5 D、 $\sqrt{8} \div \sqrt{2}$ =4

查看试题解析
5. 将方程x²- 8×+11= 0配方，则方程可变形为（）

A、（x+8）²=5 B、（x-8）²=5 C、（x-4）²=5 D、（x+4）²=5

查看试题解析
6. 电影《长津湖》讲述了一段波澜壮阔的历史，一上映就获得全国人民的追捧，全国第一天票房约3亿元，假设以后每天票房按相同的增长率增长，第三天的票房收入约4亿元，若把增长率设为x，则下列方程正确的是（）

A、（1+x）²=4 B、3（1+x）²=4 C、3（1+x）³=4 D、（1+x）³=4

查看试题解析
7. 一元二次方程2x²-3x-1= 0的根的情况是（）

A、没有实数根 B、有且只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
8. 已知y= $\sqrt{2 x - 5} + \sqrt{5 - 2 x} - 3$ ，则2xy的值为（）

A、-15 B、15 C、 $- \frac{15}{2}$ D、 $\frac{15}{2}$

查看试题解析
9. 设a= $6 \sqrt{\frac{1}{3}}$ ，b= $\frac{1}{2 - \sqrt{3}}$ ，c= $\sqrt{3} + \sqrt{2}$ ，则a，b，c的大小关系是（）

A、b>c>a B、b>a>c C、c>a>b D、a>c>b

查看试题解析
10. 《周髀算经》中有一种几何方法可以用来解形如x（x+5）= 24的方程的正数解，方法为：如图，将四个长为x+5，宽为×的长方形纸片（面积均为24）拼成一个大正方形，于是大正方形的面积为： 24×4+25= 121，边长为11，故得x（x+5）= 24的正数解为x= $\frac{11 - 5}{2}$ ，小明按此方法解关于x的方程x² + mx-n=0时，构造出同样的图形，已知大正方形的面积为10，小正方形的面积为4，则（）

A、m=2，n= $\frac{3}{2}$ B、m= $\sqrt{10}$ ，n=2 C、m= $\frac{5}{2}$ ，n=2 D、m=7，n= $\frac{3}{2}$

查看试题解析

二、填空题（本大题共6小题，共18分）

11. 要使二次根式 $\sqrt{x - 6}$ 有意义，x应满足的条件是

查看试题解析
12. 比较大小： $3 \sqrt{3}$ $2 \sqrt{6}$ （填>，<或=）．

查看试题解析
13. 若关于x的一元二次方程（a+3）x² +2x+a²-9=0有一个根为0，则a的值为

查看试题解析
14. 已知实数a在数轴上的位置如图所示，化简|a+1|+ $\sqrt{a^{2}}$ 的结果是．

查看试题解析
15. 等腰三角形的两边恰为方程x²-7x+10= 0的根，则此等腰三角形的周长为

查看试题解析
16. 某农场要建一个饲养场（矩形ABCD），两面靠现有墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两面用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图的三处各留1米宽的门（不用木栏）．建成后木栏总长45米．若饲养场的面积为180平方米，则饲养场（矩形ABCD）的一边AB的长为米．

查看试题解析

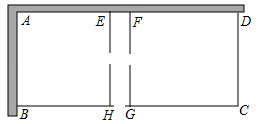
三、解答题（本大题共7小题，共52分）

17. 计算：

(1)、 $2 \sqrt{12} - \sqrt{3} + 3 \sqrt{\frac{1}{3}}$

(2)、 $(\sqrt{5} - \sqrt{2}) (\sqrt{5} + \sqrt{2}) - {(\sqrt{3} - 1)}^{2}$

查看试题解析
18. 解方程：

(1)、x²-4×+1=0

(2)、（x-3）²+2x（x-3）=0

查看试题解析
19. 在如图所示的方格图中，每个小方格的边长均为1，则△ABC的周长为多少？

查看试题解析
20. 已知x= $\sqrt{5}$ +1，y= $\sqrt{5}$ -1，求x²+2xy+y²的值．

查看试题解析
21. 已知关于x的方程ax²+2x-3=0有两个不相等的实数根．

(1)、求a的取值范围；．

(2)、若此方程的一个实数根为1，求a的值及方程的另一个实数根．

查看试题解析
22. 某水果店销售一批草莓，草莓的进价为10元/千克，市场调研发现：当草莓的售价为15元/千克时，平均每天能售出8千克，而当草莓的售价每降0.5元/千克时，平均每天能多售出4千克．

(1)、当草莓的售价定为12元/千克时，求该水果店每天草莓的销售量和销售利润．

(2)、该水果店想在每天成本不超过200元的情况下，使得每天草莓的销售利润达到64元，售价应定为多少？

查看试题解析
23. 如图，在△ABC中，∠B=90°，AB=6 $\sqrt{3}$ cm，BC=6cm，点P从点A出发，以每秒 $\sqrt{3}$ cm的速度沿AB匀速运动，同时点Q从点B出发以每秒3cm的速度沿B→C→A匀速运动，当有一点停止运动时，另一点也停止运动，设运动时间为t秒．

(1)、当t=1时，直接写出P，Q两点间的距离．

(2)、是否存在t，使得△BPQ的面积是△ABC面积的 $\frac{5}{12}$ ？若存在，请求出t的值；若不存在，请说明理由．

(3)、当△BPQ为直角三角形时，求t的取值范围．

查看试题解析