重庆市北碚区西南大学附中2021年中考数学四模试卷
试卷更新日期:2022-03-30 类型:中考模拟
一、单选题
-
1. sin60°=( )A、 B、 C、1 D、2. 某一次函数的图象与y轴交于正半轴,这个一次函数的表达式可能是( )
A、 B、 C、 D、3. 如图,AB是⊙O的直径,点D在⊙O上,若∠AOC=120°,则∠BDC的度数是( )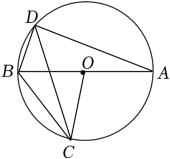 A、20° B、30° C、40° D、45°4. 函数y=中自变量x的取值范围是( )A、x≥3 B、x≤3 C、x≠3 D、x>35. 若x=2021是关于x的一元二次方程ax2﹣2bx﹣1=0的一个根,则2020﹣4042b+20212a的值为( )A、2019 B、2020 C、2021 D、20226. 下列各项变形是因式分解的是( )
A、20° B、30° C、40° D、45°4. 函数y=中自变量x的取值范围是( )A、x≥3 B、x≤3 C、x≠3 D、x>35. 若x=2021是关于x的一元二次方程ax2﹣2bx﹣1=0的一个根,则2020﹣4042b+20212a的值为( )A、2019 B、2020 C、2021 D、20226. 下列各项变形是因式分解的是( )
A、 B、 C、 D、7. 如图,在直角坐标系中,的顶点为 , , . 以点O为位似中心,在第三象限内作与的位似比为的位似图形 , 则点C的坐标为( )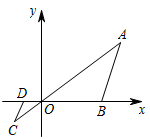 A、 B、 C、 D、8. 下列各命题是真命题的是( )A、矩形的对称轴是两条对角线所在的直线 B、平行四边形一定是中心对称图形 C、有一个内角为60°的平行四边形是菱形 D、三角形的外角等于它的两个内角之和9. 我校兴趣小组同学为测量校外“御墅临枫”的一栋电梯高层AB的楼高,从校前广场的C处测得该座建筑物顶点A的仰角为45°,沿着C向上走到30米处的D点.再测得顶点A的仰角为22°,已知CD的坡度:i=1:2,A、B、C、D在同一平面内,则高楼AB的高度为( )(参考数据;sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
A、 B、 C、 D、8. 下列各命题是真命题的是( )A、矩形的对称轴是两条对角线所在的直线 B、平行四边形一定是中心对称图形 C、有一个内角为60°的平行四边形是菱形 D、三角形的外角等于它的两个内角之和9. 我校兴趣小组同学为测量校外“御墅临枫”的一栋电梯高层AB的楼高,从校前广场的C处测得该座建筑物顶点A的仰角为45°,沿着C向上走到30米处的D点.再测得顶点A的仰角为22°,已知CD的坡度:i=1:2,A、B、C、D在同一平面内,则高楼AB的高度为( )(参考数据;sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)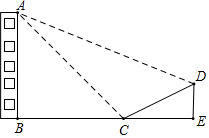 A、60 B、70 C、80 D、9010. 一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系.则点C的纵坐标是( )
A、60 B、70 C、80 D、9010. 一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系.则点C的纵坐标是( )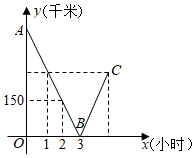 A、260 B、280 C、300 D、32011. 如果关于x的不等式组有且只有四个整数解,且关于x的分式方程的解为非负数,则符合条件的所有整数a的个数( )A、1 B、2 C、3 D、412. 如图,菱形OABC的顶点C的坐标为(3,0),D为AO上一点,连接BD,CD,OB,CD与OB相交于点E,取EC的三等分点F(EF>FC),连接OF并延长,交BC于点G,已知S△BOD:S△BOC=2:3,反比例函数y=(k>0)经过D,G两点,则k的值为( )
A、260 B、280 C、300 D、32011. 如果关于x的不等式组有且只有四个整数解,且关于x的分式方程的解为非负数,则符合条件的所有整数a的个数( )A、1 B、2 C、3 D、412. 如图,菱形OABC的顶点C的坐标为(3,0),D为AO上一点,连接BD,CD,OB,CD与OB相交于点E,取EC的三等分点F(EF>FC),连接OF并延长,交BC于点G,已知S△BOD:S△BOC=2:3,反比例函数y=(k>0)经过D,G两点,则k的值为( )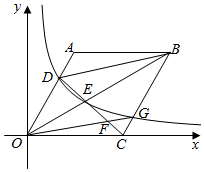 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 2020年6月23日,我国的北斗卫星导航系统(BDS)星座部署完成,其中一颗中高轨道卫星高度大约是21500000米.将数字21500000用科学记数法表示为 .14. 计算: .15. 两个人做游戏,每个人都从 , 1,这三个数中随机选择一个写在纸上,则两人所写的三个数绝对值相等的概率为 .16. 如图,已知在矩形ABCD中,AB=2,以点A为圆心,AD长为半径作 , 交AB于点E,以AB为直径的半圆恰好与DC相切,则图中阴影部分的面积为 .
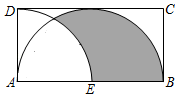 17. △ABC中,∠BAC=45°,D为AB上一点,BD=10 , 连接CD,将△CBD沿CD翻折至△CDF,点B的对应点F点恰好落在边AC上.延长CA至点E,连接DE,若AE=2,tan∠BCD= , 则DE长为 .
17. △ABC中,∠BAC=45°,D为AB上一点,BD=10 , 连接CD,将△CBD沿CD翻折至△CDF,点B的对应点F点恰好落在边AC上.延长CA至点E,连接DE,若AE=2,tan∠BCD= , 则DE长为 .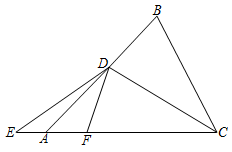 18. 为让市民感受春天,中央公园管委会决定圈出一块地打造一片花园,花园中种植桃花,樱花,李花供市民欣赏.经过一段时间,花园中已种植的桃花,樱花,李花面积之比为 . 根据市民的喜爱程度,将在花园的余下空地继续种植这三种花,经测算需将余下土地面积的种植李花,则李花种植的总面积将达到这三种花种植总面积的 . 为使桃花种植总面积与樱花种植总面积之比达到 , 则花园内种植樱花的面积与花园内种植这三种花的总面积之比是 .
18. 为让市民感受春天,中央公园管委会决定圈出一块地打造一片花园,花园中种植桃花,樱花,李花供市民欣赏.经过一段时间,花园中已种植的桃花,樱花,李花面积之比为 . 根据市民的喜爱程度,将在花园的余下空地继续种植这三种花,经测算需将余下土地面积的种植李花,则李花种植的总面积将达到这三种花种植总面积的 . 为使桃花种植总面积与樱花种植总面积之比达到 , 则花园内种植樱花的面积与花园内种植这三种花的总面积之比是 .三、解答题
-
19.(1)、(2)、20. 如图,在四边形ABCD中,AB=AD,AD//BC
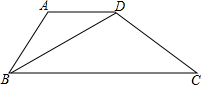 (1)、在图中,用尺规作线段BD的垂直平分线EF,分别交BD、BC于点E、F.(保留作图痕迹,不写作法)(2)、连接DF,证明四边形ABFD为菱形.21. 某公司在国内有多家门店,共有600名销售人员,为了解该公司各门店销售人员上个月的销售业绩,随机抽取了甲、乙两个门店各30名销售人员在上月的销售数量,并将数据进行整理分析,给出了下面部分信息:
(1)、在图中,用尺规作线段BD的垂直平分线EF,分别交BD、BC于点E、F.(保留作图痕迹,不写作法)(2)、连接DF,证明四边形ABFD为菱形.21. 某公司在国内有多家门店,共有600名销售人员,为了解该公司各门店销售人员上个月的销售业绩,随机抽取了甲、乙两个门店各30名销售人员在上月的销售数量,并将数据进行整理分析,给出了下面部分信息:①数据分为五组,分别为A组:x≤40,B组:40<x≤60,C组:60<x≤80,D组:80<x≤100,E组:x>100;
②样本中甲、乙两门店的最高销售数量都是120件,甲店的最低数量比乙店少两件;
③甲店C组数据:62,69,71,69,78,73,69,79,78,68
乙店C组数据:78,76,69,62,69,71,80,69,73,79,75
④两组数据的平均数、中位数、众数、极差(单位:件)如表所示:
平均数
中位数
众数
极差
甲店
70
69
69
b
乙店
70
a
69
86
⑤甲店销售数量频数分布直方图和乙店销售数量扇形统计图如下:
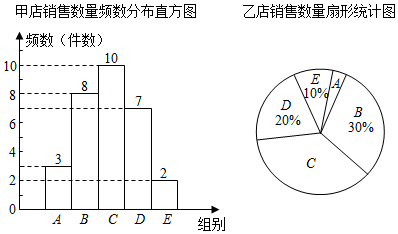 (1)、扇形统计图A组学生对应的圆心角的度数为 , 中位数a= , 极差b=;(2)、通过以上的数据分析,你认为甲、乙两个门店哪个门店的销售人员上月的业绩更好,并说明理由;(3)、若该公司计划将上月销售数量在80件以上(不含80)的员工评为“优秀销售员”,请你估计该公司能评为“优秀销售员”的人数.22. 有这样一个问题:探究函数y=的图象与性质,小童根据学习函数的经验,对函数的图象与性质进行例研究,已知当x=2时,y=7,时,y=﹣3.下面是小童探究的过程,请补充完整:
(1)、扇形统计图A组学生对应的圆心角的度数为 , 中位数a= , 极差b=;(2)、通过以上的数据分析,你认为甲、乙两个门店哪个门店的销售人员上月的业绩更好,并说明理由;(3)、若该公司计划将上月销售数量在80件以上(不含80)的员工评为“优秀销售员”,请你估计该公司能评为“优秀销售员”的人数.22. 有这样一个问题:探究函数y=的图象与性质,小童根据学习函数的经验,对函数的图象与性质进行例研究,已知当x=2时,y=7,时,y=﹣3.下面是小童探究的过程,请补充完整: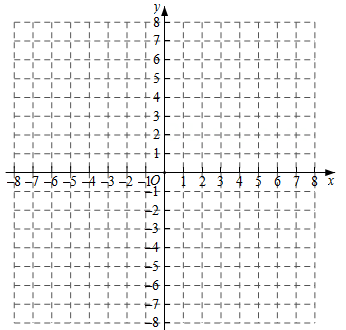 (1)、该函数的解析式为 , m= , n= .
(1)、该函数的解析式为 , m= , n= .根据图中描出的点,画出函数图象.
x
…
﹣4
﹣3
﹣2
0
2
3
4
…
y
…
m
﹣3
7
n
…
(2)、根据函图象,下列关于函数性质的描述正确的是 ;①该函数图象是中心对称图形,它的对称中心是原点.
②该函数既无最大值也无最小值.
③在自变量的取值范围内,y随x的增大而减小.
(3)、请结合(1)中函数图象,直接写出关于x的不等式的解集.(保留1位小数,误差不超过0.2)23. 为保护人类赖以生存的生态环境,中国植树节定于每年的3月12日,通过立法确定的节日.今年3月某县举办了大型植树活动,现有相邻得A、B两个社区计划共种植78棵,已知A社区每天可以种植6棵树,B社区每天可以种植12棵树.(1)、由于人员调动,要求B社区种植天数至少是A社区种植天数的1倍,当种植结束时,A社区至多种植多少天?(2)、A、B两个社区种植一棵树的所需费用分别为500元和750元,在(1)问A社区最多种植天数基础上,B社区最少种植了5天.在实际种植过程中,社区决定加大投入,种更多的树,总费用共投入67500元,种植天数比(1)问中A社区最多天数多5a%,B社区每天种植棵树下降a%,种植天数比(1)问中B社区最少种天数多(a+30)%,求a的值.24. 定义:对任意一个三位数a,如果a满足百位数字与十位数字相同,个位数字与十位数字不相同,且都不为零,那么称这个三位数为“半异数”,将一个“半异数”的各个数位上的数字交换后得到新的三位数,把所有的新三位数的和与111的商记为f(a).例如:a=112,a为“半异数”,将a各个数位上的数字交换后得到新的三位数有121、211、112,所有新三位数的和为121+211+112=444,和与111的商为444÷111=4.所以f(112)=4,根据以上定义,回答下列问题:(1)、计算f(227);(2)、数p,q是两个三位数,它们都有“半异数”,p的个位数是3,q的个位数字是5,p≤q.规定 , 若f (p)+f(q)的和是13的倍数,求k的最大值.25. 如图1,在平面直角坐标系中,抛物线与x轴交于点A(3,0),B(﹣1,0),与y轴交于C点,且OC=3OB,连接OD.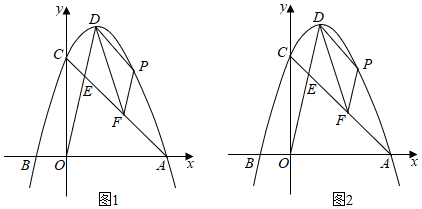 (1)、求抛物线解析式;(2)、P点为抛物线上AD部分上一动点,过P点作PF∥DE交AC于F点,求四边形DPAF面积的最大值及此时P点坐标.(3)、在(2)问的情况下,把抛物线向右平移两个单位长度,在平面内找一个点N,使以D、P、M、N为顶点的四边形为矩形26. 如图1,在等腰Rt△ABC中,∠ABC=90°,AB=BC=6,过点B作BD⊥AC交AC于点D,点E、F分别是线段AB、BC上两点,且BE=BF,连接AF交BD于点Q,过点E作EH⊥AF交AF于点P,交AC于点H.
(1)、求抛物线解析式;(2)、P点为抛物线上AD部分上一动点,过P点作PF∥DE交AC于F点,求四边形DPAF面积的最大值及此时P点坐标.(3)、在(2)问的情况下,把抛物线向右平移两个单位长度,在平面内找一个点N,使以D、P、M、N为顶点的四边形为矩形26. 如图1,在等腰Rt△ABC中,∠ABC=90°,AB=BC=6,过点B作BD⊥AC交AC于点D,点E、F分别是线段AB、BC上两点,且BE=BF,连接AF交BD于点Q,过点E作EH⊥AF交AF于点P,交AC于点H.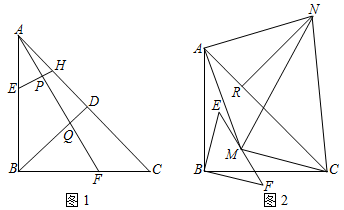 (1)、若BF=4,求△ADQ的面积;(2)、求证:CH=2BQ;(3)、如图2,BE=3,连接EF,将△EBF绕点B在平面内任意旋转,取EF的中点M,连接AM,CM,将线段AM绕点A逆时针旋转90°得线段AN,连接MN、CN,过点N作NR⊥AC交AC于点R,当线段NR的长最小时,直接写出△CMN的周长.
(1)、若BF=4,求△ADQ的面积;(2)、求证:CH=2BQ;(3)、如图2,BE=3,连接EF,将△EBF绕点B在平面内任意旋转,取EF的中点M,连接AM,CM,将线段AM绕点A逆时针旋转90°得线段AN,连接MN、CN,过点N作NR⊥AC交AC于点R,当线段NR的长最小时,直接写出△CMN的周长.