陕西省西安市2022届高三下学期理数第二次质量检测试卷
试卷更新日期:2022-03-30 类型:高考模拟
一、单选题
-
1. 若集合 , , 则( )A、 B、 C、 D、2. 为虚数单位,若复数 , 则实数的值为( )A、-1 B、0 C、 D、13. 已知都是实数,则“”是“”的( )A、充要条件 B、必要不充分条件 C、充分不必要条件 D、即不充分也不必要条件4. 已知双曲线的一条渐近线与轴正半轴所成夹角为 , 则的离心率为( )A、 B、2 C、 D、35. 按照国家标准,教室内空气中二氧化碳日平均最高容许浓度应小于等于0.1%经测定,刚下课时,空气中含有0.2%的二氧化碳,若开窗通风后教室内二氧化碳的浓度为 , 且随时间(单位:分钟)的变化规律可以用函数描述,则该教室内的二氧化碳浓度达到国家标准至少需要的时间为( )(参考数据)A、8.8分钟 B、11分钟 C、13.2分钟 D、22分钟6. 如果函数y=3cos(2x+φ)的图象关于点对称,那么|φ|的最小值为( )A、 B、 C、 D、7. 如图,在正方体中,E为棱的中点,用过点的平面截去该正方体的上半部分,则剩余几何体的侧视图为( )
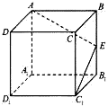 A、
A、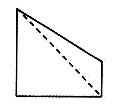 B、
B、 C、
C、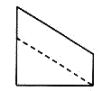 D、
D、 8. 在区间[-2,2]随机取一个数 , 则事件“ , 且”发生的概率为( )A、 B、 C、 D、9. 已知 ,若 ,则( )A、 B、 C、 D、10. 在中,角所对应的边分别为 , 则( )A、 B、 C、 D、11. 有6名医生到3个医院去作新冠肺炎治疗经验交流,则每个医院至少去一名的不同分派方法种数为( )A、216 B、729 C、540 D、42012. 已知椭圆的两焦点为 , 以为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为( )A、 B、 C、 D、
8. 在区间[-2,2]随机取一个数 , 则事件“ , 且”发生的概率为( )A、 B、 C、 D、9. 已知 ,若 ,则( )A、 B、 C、 D、10. 在中,角所对应的边分别为 , 则( )A、 B、 C、 D、11. 有6名医生到3个医院去作新冠肺炎治疗经验交流,则每个医院至少去一名的不同分派方法种数为( )A、216 B、729 C、540 D、42012. 已知椭圆的两焦点为 , 以为边作正三角形,若椭圆恰好平分正三角形的另两条边,则椭圆的离心率为( )A、 B、 C、 D、二、填空题
-
13. 若 , , 与的夹角为 , 则.14. 已知倾斜角为的直线与曲线相切,则直线的方程是.15. 已知函数 , 若关于的方程在内有唯一实根,则实数的取值范围是.16. 已知正方体 的棱长为2,以A为球心, 为半径的球面与平面A1B1C1D1的交线长为.
三、解答题
-
17. 某学校共有1000名学生,其中男生400人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了100名学生进行调查,月消费金额分布在950元之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示,将月消费金额不低于750元的学生称为“高消费群”.

(参考公式: , 其中
(1)、求的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);(2)、若样本中属于“高消费群”的女生有20人,完成下列列联表,并判断是否有97.5%的把握认为该校学生属于“高消费群”与“性别”有关?属于“高消费群”
不属于“高消费群”
合计
男
女
合计
18. 在公比为2的等比数列中,成等差数列.(1)、求数列的通项公式;(2)、若 , 求数列的前项和.19. 如图, 为圆锥的顶点, 为底面圆心,点 , 在底面圆周上,且 , 点C,D分别为SB,OB的中点. (1)、求证: ;(2)、若圆锥的底面半径为2,高为4,求直线 与平面 所成的角的正弦值.20. 已知定点 , 定直线 , 动圆过点 , 且与直线相切.(1)、求动圆的圆心轨迹的方程;(2)、过焦点的直线与抛物线交于两点,与圆交于两点(A,C在y轴同侧),求证:是定值.
(1)、求证: ;(2)、若圆锥的底面半径为2,高为4,求直线 与平面 所成的角的正弦值.20. 已知定点 , 定直线 , 动圆过点 , 且与直线相切.(1)、求动圆的圆心轨迹的方程;(2)、过焦点的直线与抛物线交于两点,与圆交于两点(A,C在y轴同侧),求证:是定值.