山西省长治市名校2022届高三下学期理数模拟试卷

试卷更新日期：2022-03-30 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $P = {s | s = 2 k + 1 ， k \in Z} ， Q = {s | s = 4 k + 1 ， k \in Z}$ ，则 $P ∩ Q =$ （）

A、P B、Q C、Z D、 $\emptyset$

查看试题解析
2. 若 $z = \frac{i}{3 i + 1}$ ，则 $| z | =$ （）

A、 $\frac{1}{10}$ B、10 C、 $\frac{\sqrt{10}}{10}$ D、 $\sqrt{10}$

查看试题解析
3. 命题 $p ： \exists x \leq 0 ， x^{2} - 2 x + e > 1$ ，则 $\neg p$ 为（）

A、 $\exists x > 0 ， x^{2} - 2 x + e \leq 1$ B、 $\exists x \leq 0 ， x^{2} - 2 x + e \leq 1$ C、 $\forall x > 0 ， x^{2} - 2 x + e \leq 1$ D、 $\forall x \leq 0 ， x^{2} - 2 x + e \leq 1$

查看试题解析
4. 若函数 $f (x)$ 满足 $f (x + 2) = f (x)$ ，则 $f (x)$ 可以是（）

A、 $f (x) = (x - 1)^{2}$ B、 $f (x) = | x - 2 |$ C、 $f (x) = s i n (\frac{π}{2} x)$ D、 $f (x) = t a n (\frac{π}{2} x)$

查看试题解析
5. 如图，某几何体平面展开图由一个等边三角形和三个等腰直角三角形组合而成，E为 $B C$ 的中点，则在原几何体中，异面直线 $A E$ 与 $C D$ 所成角的余弦值为（）

A、 $\frac{\sqrt{6}}{6}$ B、 $\frac{\sqrt{6}}{3}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{6}}{12}$

查看试题解析
6. $(x^{2} - 2 x + \frac{1}{x}) {(1 - \frac{2}{\sqrt{x}})}^{5}$ 展开式中常数项为（）

A、-15 B、0 C、15 D、80

查看试题解析
7. 已知 $α \in (- π ， 0)$ ，且 $3 c o s 2 α - 2 s i n α c o s α - 3 = 0$ ，则 $s i n α =$ （）

A、 $\frac{3 \sqrt{10}}{10}$ B、 $\frac{\sqrt{10}}{10}$ C、 $- \frac{3 \sqrt{10}}{10}$ D、 $- \frac{\sqrt{10}}{10}$

查看试题解析
8. 从装有3个白球m个红球n个黄球（这些小球除颜色外完全相同）的布袋中任取两个球，记取出的白球的个数为X，若 $E (X) = \frac{3}{5}$ ，取出一白一红的概率为 $\frac{1}{3}$ ，则取出一红一黄的概率为（）

A、 $\frac{2}{9}$ B、 $\frac{1}{3}$ C、 $\frac{4}{15}$ D、 $\frac{1}{5}$

查看试题解析
9. 函数 $f (x) = A s i n (ω x + φ) (ω > 0 ， 0 < φ < π)$ 的图象过点 $(0 ， 1)$ ，距离y轴最近的最高点是 $P (\frac{π}{9} ， 2)$ ，则下列说法正确的是（）

A、 $ω = 2$ B、函数 $f (x)$ 在区间 $(- \frac{π}{3} ， 0)$ 内单调递增 C、函数 $f (x)$ 关于点 $(\frac{5 π}{18} ， 0)$ 对称 D、若函数 $f (x)$ 的图象向右平移 $\frac{π}{6}$ 个单位后得到 $g (x)$ 的图象，则 $g (x)$ 是奇函数

查看试题解析
10. 当 $a > 0$ 时，过点 $(a ， a + b)$ 均可以作曲线 $y = l n x$ 的两条切线，则b的取值范围是（）

A、 $(- \infty ， - 1)$ B、 $(- \infty ， - 1]$ C、 $(- 1 ， + \infty)$ D、 $[- 1 ， + \infty)$

查看试题解析
11. 过点P作抛物线 $C ： x^{2} = 4 y$ 的切线 $l_{1} ， l_{2}$ ，切点分别为 $M ， N$ ，若 $△ P M N$ 的重心坐标为 $(3 ， 4)$ ，且P在抛物线 $D ： y^{2} = a x$ 上，则D的焦点坐标为（）

A、 $(\frac{3}{4} ， 0)$ B、 $(\frac{3}{2} ， 0)$ C、 $(3 ， 0)$ D、 $(1 ， 0)$

查看试题解析
12. 若 $n \in N^{*}$ ，满足 $\frac{n + 2}{n + 1} < e^{0.01} < \frac{n + 1}{n}$ ，则 $n =$ （）

A、98 B、99 C、100 D、101

查看试题解析

二、填空题

13. 已知向量 $\vec{a} = (1 ， 2) ， \vec{b} = (0 ， 1)$ ，若 $(\vec{a} - \vec{b}) ⊥ (\vec{a} + λ \vec{b})$ ，则 $λ =$ .

查看试题解析
14. 在 $△ A B C$ 中， $∠ B A C = 90 ° ， A B = 3 \sqrt{3} ， A C = 3$ ，点D在线段 $B C$ 上，且 $A D = \sqrt{7}$ ，则 $B D =$ .

查看试题解析
15. 如图，在三棱锥 $P - A B C$ 中，平面 $E F M N$ 平行于对棱 $A C ， P B ， A C = P B = 2 ， A C ⊥ P B$ ，截面 $E F M N$ 面积的最大值是.

查看试题解析
16. 已知 $F_{1} ， F_{2}$ 分别为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的两个焦点，曲线上的点P到原点的距离为b，且 $s i n ∠ P F_{2} F_{1} = 2 s i n ∠ P F_{1} F_{2}$ ，则该双曲线的离心率为.

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n} ， a_{1} = 1 ， \frac{S_{n}}{n} = a_{n + 1} - n - 1 ， n \in N^{*}$ .

(1)、证明 ${\frac{S_{n}}{n}}$ 为等差数列，并求 ${S_{n}}$ 的通项公式；

(2)、若 $c_{n} = \frac{(a_{n} + 1) \cdot 3^{n}}{2} (n \in N^{*})$ ，求数列 ${c_{n}}$ 的前n项和 $T_{n}$ .

查看试题解析
18. 三棱锥 $P - A B C$ 中，△ $P A C$ 为等腰直角三角形， $P A = P C = \frac{1}{2} A B = 2 ， P B = 2 \sqrt{3}$ ，平面 $P A C ⊥$ 平面 $A B C$ .

(1)、求证： $P A ⊥ B C$ ；

(2)、求 $P C$ 和平面 $P A B$ 所成角的正弦值.

查看试题解析
19. 山西运城王过酥梨是国家农产品地理标志保护产品，王过酥梨含有多种对人体有益的钙、铁、磷等微量营养元素，食后清火润肺，止咳化痰，能起到祛病养生之效，一致被人们作为逢年过节走亲访友，馈赠待客及日常生活的必备佳品.某水果批发商小李从事酥梨批发多年，他把去年年底客户采购酥梨在 $[100 ， 200]$ 内的数量x（单位：箱）绘制成下表：
采购数x（单位：箱）
$[100 ， 120)$
$[120 ， 140)$
$[140 ， 160)$
$[160 ， 180)$
$[180 ， 200]$
客户数
5
10
15
15
5

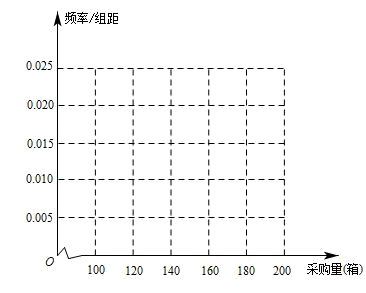(1)、根据表中的数据，补充完整这些数据的频率分布直方图，并估计采购数在168箱以上（含168箱）的客户数；

(2)、若去年年底采购在 $[100 ， 200]$ 内的酥梨数量约占小李去年年底酥梨总销售量的 $\frac{4}{5}$ ，估算小李去年年底总销售量（同一组中的数据用该组区间的中点值作代表）；

(3)、在（2）的条件下，由于酥梨受到人们的青睐，小李做了一份市场调查以决定今年年底是否在网上出售酥梨，若没有在网上出售酥梨，则按去年的价格出售，每箱利润为14元，预计销售量与去年持平；若计划在网上出售酥梨，则需把每箱售价下调1至5元（网上、网下均下调），且每下调m元 $(1 \leq m \leq 5 ， m \in Z)$ 销售量可增加 $950 m$ 箱，试预计小李在今年年底销售酥梨总利润Y（单位：元）的最大值.

查看试题解析
20. 已知函数 $f (x) = x l n x$ .

(1)、证明： $f (x) \geq x - 1$ ；

(2)、若 $f (x) = a$ 有两个不相等的实数根 $x_{1} ， x_{2}$ ，求证： $x_{1} + x_{2} < 1$ .

查看试题解析
21. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{1}{2}$ ，左，右焦点分别为 $F_{1} ， F_{2} ， O$ 为坐标原点，点Q在椭圆C上，且满足 $| Q F_{1} | + | Q F_{2} | = 4$ .

(1)、求椭圆C的标准方程；

(2)、P为椭圆C的右顶点，设直线 $l$ 与椭圆C交于异于点P的 $M ， N$ 两点，且 $P M ⊥ P N$ ，求 $| P M | \cdot | P N |$ 的最大值.

查看试题解析
22. 在直角坐标系 $x O y$ 中，以坐标原点为极点，以x轴正半轴为极轴，建立极坐标系，直线 $l$ 的极坐标方程为 $ρ c o s (θ - \frac{π}{3}) = \frac{\sqrt{3}}{2}$ ，曲线C的极坐标方程为 $ρ^{2} (3 - c o s 2 θ) = 8$ .

(1)、写出直线 $l$ 和曲线C的直角坐标方程；

(2)、已知点 $P (\sqrt{3} ， 0)$ ，若直线 $l$ 与画线C交于 $A ， B$ 两点，求 $\frac{1}{| P A |} + \frac{1}{| P B |}$ 的值.

查看试题解析
23. 已知 $f (x) = | 2 x - a^{2} |$ .

(1)、当 $a = 1$ 时，求不等式 $f (x) + | x + 1 | \geq 3$ 的解集；

(2)、若对于任意实数x，不等式 $| 2 x - 3 | - f (x) < 2 a$ 成立，求实数a的取值范围.

查看试题解析

采购数x（单位：箱）	$[100 ， 120)$	$[120 ， 140)$	$[140 ， 160)$	$[160 ， 180)$	$[180 ， 200]$
客户数	5	10	15	15	5