北师大版备考2022中考数学二轮复习专题8 一元一次不等式(组)
试卷更新日期:2022-03-29 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 已知x≤y下列式子中成立的是( )A、 B、 C、 D、2. 已知关于 的不等式组 的整数解共有3个,则 的取值范围是( )A、 B、 C、 D、3. 已知某程序如图所示,规定:从“输入实数x”到“结果是否大于95”为一次操作,如果该程序进行了两次操作停止,那么实数x的取值范围是
 A、 B、 C、 D、4. 如图,直线k∥l, .其中 , ,则 的最大整数值是( )
A、 B、 C、 D、4. 如图,直线k∥l, .其中 , ,则 的最大整数值是( ) A、108° B、110° C、114° D、115°5. 关于x的不等式 的整数解只有4个,则m的取值范围是( )A、 B、 C、 D、6. 关于 的不等式组 恰有五个整数解,那么m的取值范围为( )A、 B、 C、 D、7. 等腰三角形ABC中,AB=AC , 记AB=x , 周长为y , 定义(x , y)为这个三角形的坐标,如图所示,直线 将第一象限划分为4个区域,下面四个结论中:
A、108° B、110° C、114° D、115°5. 关于x的不等式 的整数解只有4个,则m的取值范围是( )A、 B、 C、 D、6. 关于 的不等式组 恰有五个整数解,那么m的取值范围为( )A、 B、 C、 D、7. 等腰三角形ABC中,AB=AC , 记AB=x , 周长为y , 定义(x , y)为这个三角形的坐标,如图所示,直线 将第一象限划分为4个区域,下面四个结论中:①对于任意等腰三角形ABC , 其坐标不可能位于区域Ⅰ中;②对于任意等腰三角形ABC , 其坐标可能位于区域Ⅳ;③若三角形ABC是都能腰直角三角形,其坐标位于区域Ⅲ中;④图中点M所对应等腰三角形的底边比点N所对应等腰三角形的底边长所有正确的结论序号是( )
 A、①③ B、①③④ C、②④ D、①②③8. 如图,函数y=kx和y=﹣ x+4的图象相交于点A(3,m)则不等式kx≥﹣ x+4的解集为( )
A、①③ B、①③④ C、②④ D、①②③8. 如图,函数y=kx和y=﹣ x+4的图象相交于点A(3,m)则不等式kx≥﹣ x+4的解集为( )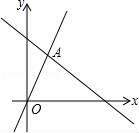
 A、x≥3 B、x≤3 C、x≤2 D、x≥29. 已知点A(-1,3),点B(-1,-4),若常数a使得一次函数y=ax+1与线段AB有交点,且使得关于x的不等式组 无解,则所有满足条件的整数a的个数为( )A、3 B、4 C、5 D、610. 如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)<0的解集为( )
A、x≥3 B、x≤3 C、x≤2 D、x≥29. 已知点A(-1,3),点B(-1,-4),若常数a使得一次函数y=ax+1与线段AB有交点,且使得关于x的不等式组 无解,则所有满足条件的整数a的个数为( )A、3 B、4 C、5 D、610. 如图,直线y=kx+b与y=mx+n分别交x轴于点A(﹣0.5,0)、B(2,0),则不等式(kx+b)(mx+n)<0的解集为( )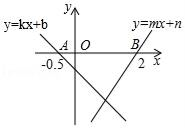 A、x>2 B、﹣0.5<x<2 C、0<x<2 D、x<﹣0.5或x>2
A、x>2 B、﹣0.5<x<2 C、0<x<2 D、x<﹣0.5或x>2二、解答题(共78分)
-
11. 先化简,再求值: ,其中 为整数且满足不等式组12. 当x的取值范围是不等式组 的解时,试化简: .13. 解不等式组 , 并把解集表示在数轴上.
 14. 解下列不等式组(1)、(2)、(3)、(4)、(5)、15. 阅读材料:基本不等式 ,当且仅当 时,等号成立.其中我们把 叫做正数a、b的算术平均数, 叫做正数a、b的几何平均数,它是解决最大 小 值问题的有力工具.
14. 解下列不等式组(1)、(2)、(3)、(4)、(5)、15. 阅读材料:基本不等式 ,当且仅当 时,等号成立.其中我们把 叫做正数a、b的算术平均数, 叫做正数a、b的几何平均数,它是解决最大 小 值问题的有力工具.例如:在 的条件下,当x为何值时, 有最小值,最小值是多少?
解 ,
,即是
,
当且仅当 时,即 时, 有最小值,最小值为2.
请根据阅读材料解答下列问题:
(1)、若 ,函数 ,当x为何值时,函数有最值,并求出其最值,(2)、当 时,式子 成立吗?请说明理由.16. 深化理解:新定义:对非负实数x“四舍五入”到个位的值记为<x>,
即:当n为非负整数时,如果n﹣ ≤x<n+ ,则<x>=n;
反之,当n为非负整数时,如果<x>=n,则n﹣ ≤x<n+ .
例如:<0>=<0.48>=0,<0.64>=<1.49>=1,<2>=2,<3.5>=<4.12>=4,…
试解决下列问题:
(1)、填空:①<π>=(π为圆周率); ②如果<x﹣1>=3,则实数x的取值范围为 .(2)、若关于x的不等式组 的整数解恰有3个,求a的取值范围.(3)、求满足<x>= x 的所有非负实数x的值.17. 阅读材料:基本不等式 当且仅当a=b时,等号成立,其中我们把 叫做正数a,b的算术平均数, 叫做正数a,b的几何平均数,它是解决最大(小)值问题的有力工具,例如:在x>0的条件下,当x为何值时, 有最小值?最小值是多少?解:∵x>0, ,∴ ≥2 ,∴ ,当且仅当 时,即x=1时,有 有最小值为2.
请根据阅读材料解答下列问题:
(1)、填空:当 >0时,设 ,则当且仅当 =时,y有最值为;(2)、若 >0,函数 ,当x为何值时,函数有最值?并求出其最值;(3)、在Rt△ABC中,∠C=90°,若△ABC的面积等于8,求△ABC周长的最小值.18. 定义:对任意一个两位数a,如果a满足个位数字与十位数字互不相同,且都不为零,那么称这个两位数为“湘一数”.将一个“湘一数”的个位数字与十位数字对调后得到一个新的两位数,把这个两位数与原两位数的和与11的商记为 .例如:a=23,对调个位数字与十位数字得到新两位数32,新两位数与原两位数的和为23+32=55,和与11的商为55÷11=5,所以 .根据以上定义,回答下列问题:
(1)、填空:①下列两位数:50、42,33中,“湘一数”为;②计算: .(2)、如果一个“湘一数”b的十位数字是k,个位数字是 ,且 ,请求出“湘一数”b;(3)、如果一个“湘一数”c,满足 ,求满足条件的c的值.19. 现计划把甲种货物306吨和乙种货物230吨运往某地.已知有A、B两种不同规格的货车共50辆,如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨,每辆B型货车最多可装甲种货物5吨和乙种货物7吨.(1)、装货时按此要求安排A、B两种货车的辆数,共有几种方案?(2)、使用A型车每辆费用为600元,使用B型车每辆费用800元.在上述方案中,哪个方案运费最省?最省的运费是多少元?(3)、在(2)的方案下,现决定对货车司机发共2100元的安全奖,已知每辆A型车奖金为m元.每辆B型车奖金为n元,38<m<n.且m、n均为整数,求此次奖金发放的具体方案.