2022年中考数学二轮专题复习-分式、根式

试卷更新日期：2022-03-29 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列式子是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{3}$ C、 $\sqrt{9}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 如果分式 $\frac{x^{2} - 4}{x^{2} - 4 x + 4}$ 的值为0，则 $x$ 的值为（）

A、-2 B、2 C、±2 D、不存在

查看试题解析
3. 在实数范围内要使 $\sqrt{{(a - 2)}^{2}} = a - 2$ 成立，则a的取值范围是（　　　）

A、a=2 B、 $a > 2$ C、 $a \geq 2$ D、 $a \leq 2$

查看试题解析
4. 下列约分正确的是（）

A、 $\frac{x^{6}}{x^{2}} = x^{3}$ B、 $\frac{x^{2} + y^{2}}{x + y} = x + y$ C、 $\frac{x + m}{y + m} = \frac{x}{y}$ D、 $\frac{15 b - 5 a}{2 a - 6 b} = - \frac{5}{2}$

查看试题解析
5. 估计 $(\sqrt{24} + \sqrt{6}) \div \sqrt{2}$ 的值应在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
6. 如果 $m^{2} - 2 m - 2 = 0$ ，那么代数式 $(m - \frac{4 m - 4}{m})$ . $\frac{m^{2}}{2 - m}$ 的值是（）

A、-2 B、-1 C、2 D、3

查看试题解析
7. 如图，在长方形ABCD中无重叠放人面积分别为 $16 {cm}^{2}$ 和 $12 {cm}^{2}$ 的两张正方形纸片，则图中空白部分的面积为（）

A、 $(- 12 + 8 \sqrt{3}) {cm}^{2}$ B、 $(16 - 8 \sqrt{3}) {cm}^{2}$ C、 $(8 - 4 \sqrt{3}) {cm}^{2}$ D、 $(4 - 2 \sqrt{3}) {cm}^{2}$

查看试题解析
8. 若x= $\frac{2y}{3}$ ，则 $\frac{x}{y}$ ＝（）

A、 $\frac{1}{6}$ B、6 C、 $\frac{3}{2}$ D、 $\frac{2}{3}$

查看试题解析
9. 已知 $a + b = 5$ ， $a b = 3$ ，则 $\frac{b}{a} + \frac{a}{b}$ 的值为（）

A、6 B、 $\frac{19}{3}$ C、 $\frac{22}{3}$ D、8

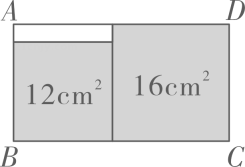查看试题解析
10. 计算 $\frac{x}{a + 1} \cdot \frac{a^{2} - 1}{2 x}$ 的结果正确的是（）

A、 $\frac{a - 1}{2}$ B、 $\frac{a + 1}{2}$ C、 $\frac{a - 1}{2 x}$ D、 $\frac{a + 1}{2 a + 2}$

查看试题解析
11. 已知x为整数，且 $\frac{1}{x + 3} + \frac{1}{x - 3} + \frac{x + 9}{x^{2} - 9}$ 为整数，则符合条件的x有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
12. 如图，已知钓鱼竿AC的长为6 m，露在水面上的渔线BC长为3 $\sqrt{2}$ m，某钓鱼者想看看鱼钩上的情况，把鱼竿AC转动到AC'的位置，此时露在水面上的渔线B'C'为 $\sqrt{34}$ m，则BB'的长为（）

A、 $\sqrt{2}$ m B、2 $\sqrt{2}$ m C、 $\sqrt{5}$ m D、2 $\sqrt{3}$ m

查看试题解析
13. 若ab＝1，m＝ $\frac{1}{1 + a} + \frac{1}{1 + b}$ ，则m²⁰²¹的值为（　　）

A、1 B、﹣1 C、2 D、﹣2

查看试题解析
14. 已知：m， n是两个连续自然数（m<n），且q=mn，设 $p = \sqrt{q + n} + \sqrt{q - m}$ ，则p( )。

A、总是奇数 B、总是偶数 C、有时奇数，有时偶数 D、有时有理数，有时无理数

查看试题解析
15. 对于任意的正数m、n定义运算※为：m※n= $\{\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ ，计算（3※2）×（8※12）的结果为（　　）

A、2﹣4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析

二、填空题

16. 计算：（ $2 \sqrt{5}$ -3）（ $2 \sqrt{5}$ +3）=.

查看试题解析
17. 若2x=5y，则 $\frac{x + y}{x} =$ .

查看试题解析
18. 已知a，b都是实数，若 $\sqrt{a - 2}$ +（b+1）²=0，则a-b=

查看试题解析
19. 已知长方形的面积为12，共中一边长为 $2 \sqrt{2}$ ，则该长方形的另一边长为．

查看试题解析
20. 已知 $a + b = - 3 a b$ ，则 $\frac{a b}{3 a + 3 b - a b} =$ .

查看试题解析
21. 已知a=-2² ， b=（-3）^-2 ， c=-3⁰ ，则将a，b，c按从小到大的顺序排列为.

查看试题解析
22. $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ 是物理学中的一个公式，其中各个字母都不为零且 $R_{1} + R_{2} \neq 0$ ．用 $R_{1} ， R_{2}$ 表示R，则R＝

查看试题解析
23. 当 $x = \frac{1}{2}$ 时，计算 $\frac{x^{2} - 4 x + 4}{x^{2} - 4} \div \frac{x - 2}{x^{2} + 2 x}$ 的结果等于．

查看试题解析
24. 若|a﹣1|+（ab﹣2）²＝0，则 $\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)}$ $+$ … $+$ $\frac{1}{(a + 10) (b + 10)}$ ＝.

查看试题解析
25. 若实数x，y，m满足等式 $\sqrt{3 x + 5 y - 3 - m} + {(2 x + 3 y - m)}^{2}$ $= \sqrt{x + y - 2} - \sqrt{2 - x - y}$ ，则m+4的算术平方根为．

查看试题解析

三、计算题

26. 计算：
① $\sqrt{7^{2}}$ =

② $\sqrt{{(\frac{1}{3})}^{2}}$ =

③ $\sqrt{{2.1}^{2}}$ =

④ $\sqrt{{(- 7)}^{2}}$ =

⑤ $\sqrt{{(- \frac{1}{3})}^{2}}$ =

⑥ $\sqrt{{(- 2.1)}^{2}}$ =

查看试题解析
27. 计算．

(1)、 $- 1^{100} + \sqrt[3]{64} - {(\frac{1}{2})}^{- 1} + {(π - 3.14)}^{0}$

(2)、 ${(- 2 x^{3})}^{2} \cdot (- x^{2}) \div {[{(- x)}^{2}]}^{3}$

查看试题解析
28.

(1)、 $\sqrt{18} \times \sqrt{2} - \frac{\sqrt{98}}{\sqrt{2}}$

(2)、 ${(\sqrt{3} - 2)}^{2} - \frac{\sqrt{54} - \sqrt{24}}{\sqrt{2}}$

查看试题解析
29. 先化简，再求值：

(1)、 $\frac{2 x}{x^{2} - 9} - \frac{1}{x - 3}$ ，其中x＝4.

(2)、(a＋b)(a－b)＋(4ab³－8a²b²)÷4ab，其中a＝2，b＝1．

查看试题解析
30. 已知abc≠0且a+b+c=0，求a $(\frac{1}{b} + \frac{1}{c})$ +b $(\frac{1}{c} + \frac{1}{a})$ +c $(\frac{1}{a} + \frac{1}{b})$ 的值.

查看试题解析
31. 若x ， y为实数，且y＝ $\sqrt{1 - 4 x}$ ＋ $\sqrt{4 x - 1}$ ＋ $\frac{1}{2}$ ．求 $\sqrt{\frac{x}{y} + 2 + \frac{y}{x}}$ － $\sqrt{\frac{x}{y} - 2 + \frac{y}{x}}$ 的值．

查看试题解析
32. 先化简，再求值： $\frac{a^{3} - a}{a^{2} + 2 a + 1} \div \frac{a - 1}{2 a + 2} + (1 + \frac{2}{a} - \frac{a + 1}{a - 2}) \cdot \frac{2 a^{3} - 4 a^{2}}{a + 1}$ ，其中a的值在0，1，﹣1，2，5中选出一个合适的值．

查看试题解析
33. 阅读材料
$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \frac{\sqrt{3} - \sqrt{2}}{{(\sqrt{3})}^{2} - {(\sqrt{2})}^{2}} = \sqrt{3} - \sqrt{2}$ ，像上述解题过程中， $\sqrt{3} + \sqrt{2}$ 和 $\sqrt{3} - \sqrt{2}$ 相乘的积不含二次根式，我们可以将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化。

(1)、化简
① $\frac{4}{\sqrt{15} + \sqrt{11}}$ ；

② $\frac{2}{\sqrt{2 n + 1} + \sqrt{2 n - 1}}$ （n为整数）；

(2)、化简： $\frac{2}{\sqrt{3} + 1} + \frac{2}{\sqrt{5} + \sqrt{3}} + \frac{2}{\sqrt{7} + \sqrt{5}} + \dots + \frac{2}{\sqrt{101} + \sqrt{99}}$

查看试题解析

四、解答题

34. 先化简，再求值： $(\frac{4 x y}{x - 2 y} + x) \div \frac{x^{2} + 4 x y + 4 y^{2}}{4 y^{3} - x^{2} y}$ ，其中 $| 2 x - 1 | + y^{2} + 4 y + 4 = 0$

查看试题解析
35. 先化简，再求值：（a²+4a）÷（ $\frac{a^{2} - 9}{a^{2} - 6 a + 9} - \frac{1}{3 - a}$ ），其中a是方程x²﹣3x﹣1＝0的根．

查看试题解析
36. 先化简，再求值： $\frac{b^{2}}{a^{2} - a b} \div (\frac{a^{2} - b^{2}}{a^{2} - 2 a b + b^{2}} + \frac{a}{b - a})$ ，其中 $a = {(2022 - π)}^{0}$ ， $b = \frac{1}{3}$ .

查看试题解析
37. 古希腊的几何学家海伦给出了求三角形面积的公式：S= $\sqrt{p (p - a) (p - b) (p - c)}$ ，其中a，b，c为三角形的三边长，p= $\frac{a + b + c}{2}$ ．若一个三角形的三边长分别为2，3，4，求该三角形的面积．

查看试题解析
38. 小明在解决问题：已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值，他是这样分析与解答的：
$∵ a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，

$∴ a - 2 = - \sqrt{3}$ ，

$∴ {(a - 2)}^{2} = 3$ ， $a^{2} - 4 a + 4 = 3$

$∴ a^{2} - 4 a = - 1$ .

$∴ 2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 (- 1) + 1 = - 1$ .

请你根据小明的分析过程，解决如下问题：若 $a = \frac{1}{\sqrt{2} - 1}$ ，求 $4 a^{2} - 8 a - 3$ 的值.

查看试题解析
39. 阅读下列解题过程，然后解题：
题目：已知 $\frac{x}{a - b} = \frac{y}{b - c} = \frac{z}{c - a} (a ， b ， c$ 互不相等)，求 $x + y + z$ 的值.

解：设 $\frac{x}{a - b} = \frac{y}{b - c} = \frac{z}{c - a} = k$ ，则 $x = k (a - b)$ ， $y = k (b - c) ， z = k (c - a)$ ，

$∴ x + y + z = k (a - b + b - c + c - a) = k \cdot 0 = 0$ ， $∴ x + y + z = 0$ .

依照上述方法解答下列问题：

已知 $\frac{y + z}{x} = \frac{z + x}{y} = \frac{x + y}{z}$ ，其中 $x + y + z \neq 0$ ，求 $\frac{x + y - z}{x + y + z}$ 的值.

查看试题解析
40. 先阅读下列材料，再回答相应的问题
若 $\sqrt{1 - x}$ 与 $\sqrt{x - 1}$ 同时成立，则x的值应是多少？

有下面的解题过程：

由于 $\sqrt{1 - x}$ 与 $\sqrt{x - 1}$ 都是算术平方根，故两者的被开方数 $1 - x$ 与 $x - 1$ 均为非负数.而 $1 - x$ 与 $x - 1$ 互为相反数，两个非负数互为相反数，只有一种情形，那便是 $1 - x = 0$ ， $x - 1 = 0$ 所以 $x = 1$ .

问题：已知 $y = \sqrt{1 - 2 x} + \sqrt{2 x - 1} + 2$ ，求 $x^{y}$ 的值.

查看试题解析
41. 阅读理解
“分母有理化”是我们常用的一种化简的方法： $\frac{2 + \sqrt{3}}{2 - \sqrt{3}} = \frac{(2 + \sqrt{3}) (2 + \sqrt{3})}{(2 - \sqrt{3}) (2 + \sqrt{3})} = 7 + 4 \sqrt{3}$ ，除此之外，我们也可以用平方之后再开方的方式来化简一些有特点的无理数，如：对于 $\sqrt{3 + 5 \sqrt{5}} - \sqrt{3 - 5 \sqrt{5}}$

设 $x = \sqrt{3 + 5 \sqrt{5}} - \sqrt{3 - 5 \sqrt{5}}$ ，

易知 $\sqrt{3 + 5 \sqrt{5}} > \sqrt{3 - 5 \sqrt{5}}$

故 $x > 0$ ，由 $x^{2} = {(\sqrt{3 + 5 \sqrt{5}} - \sqrt{3 - 5 \sqrt{5}})}^{2}$

$= 3 + \sqrt{5} + 3 - \sqrt{5} - 2 \sqrt{(3 + 5 \sqrt{5}) (3 - 5 \sqrt{5})}$

$= 2$

解得 $x = \sqrt{2}$ ，即 $\sqrt{3 + 5 \sqrt{5}} - \sqrt{3 - 5 \sqrt{5}} = \sqrt{2}$ ．

根据以上方法，化简 $\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}} + \sqrt{6 - 3 \sqrt{3}} - \sqrt{6 + 3 \sqrt{3}}$

查看试题解析
42. 如图，以直角三角形AOC 的直角顶点O为原点，以 OA，OC 所在直线为x轴，y轴建立平面直角坐标系，点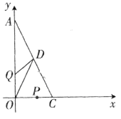 $A (0 ， a) ， C (c ， 0)$ 满足 $\sqrt{a - 2 c} + | c - 4 | = 0$

(1)、则 $C$ 点的坐标为； $A$ 点的坐标为.

(2)、直角三角形 $A O C$ 的面积为.

(3)、已知坐标轴上有两动点 $P 、 Q$ 同时出发， $P$ 点从 $C$ 点出发沿 $x$ 轴负方向以1个单位长度每秒的速度匀速移动， $Q$ 点从 $O$ 点出发以2个单位长度每秒的速度沿 $y$ 轴正方向移动，点 $Q$ 到达 $A$ 点整个运动随之结束． $A C$ 的中点 $D$ 的坐标是 $(2 ， 4)$ ，设运动时间为t（t＞0）秒，问：是否存在这样的t使 $S_{△ O D P} = S_{△ O D Q}$ ？若存在，请求出 $t$ 的值；若不存在，请说明理由.

查看试题解析