山东省淄博市临淄区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算中，正确的是（）

A、 $\sqrt{6} \div \sqrt{2} = 3$ B、 $2 + \sqrt{2} = 2 \sqrt{2}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $2 \sqrt{3} - 2 = \sqrt{3}$

查看试题解析
2. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{4 x}$ B、 $\sqrt{x^{2} - 2}$ C、 $\sqrt{3 x^{2}}$ D、 $\sqrt{\frac{x}{2}}$

查看试题解析
3. 已知 $y = \sqrt{6 x - 6} + \sqrt{6 - 6 x} - 3$ ，则 $5 x y$ 的值是（）

A、-15 B、15 C、 $- \frac{15}{2}$ D、 $\frac{15}{2}$

查看试题解析
4. 对于无理数 $\sqrt{3}$ ，添加关联的数或者运算符号组成新的式子，其运算结果能成为有理数的是（）.

A、 $2 \sqrt{3} - 3 \sqrt{2}$ B、 $\sqrt{3} + \sqrt{3}$ C、 ${(\sqrt{3})}^{3}$ D、 $0 \times \sqrt{3}$

查看试题解析
5. 一元二次方程 $2 x^{2} + 3 x + 1 = 0$ 用配方法解方程，配方结果是（）

A、 ${(x + \frac{3}{4})}^{2} = \frac{1}{16}$ B、 $2 {(x - \frac{3}{4})}^{2} = \frac{1}{8}$ C、 ${(x + \frac{3}{4})}^{2} = - \frac{1}{8}$ D、 ${(x + \frac{3}{4})}^{2} - \frac{1}{16} = - 1$

查看试题解析
6. 已知关于x的一元二次方程(a－1)x²－2x＋1=0有两个不相等的实数根，则a的取值范围是（）

A、a＞2 B、a＜2 C、a＜2且a≠1 D、a＜－2

查看试题解析
7. 已知m、n是方程x²+3x﹣2=0的两个实数根，则m²+4m+n+2mn的值为（）

A、1 B、3 C、﹣5 D、﹣9

查看试题解析
8. 如图，矩形内有两个相邻的正方形，其面积分别为2和8，则图中阴影部分的面积为（）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、6

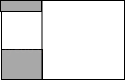查看试题解析
9. 直线 $y = x + a$ 不经过第二象限，则关于 $x$ 的方程 $a x^{2} + 2 x + 1 = 0$ 实数解的个数是（）.

A、0个 B、1个 C、2个 D、1个或2个

查看试题解析
10. 已知m、n、4分别是等腰三角形(非等边三角形)三边的长，且m、n是关于x的一元二次方程 $x^{2}$ ﹣6x+k+2=0的两个根，则k的值等于(　　)

A、7 B、7或6 C、6或﹣7 D、6

查看试题解析
11. 如图，学校课外生物小组的试验园地的形状是长35米、宽20米的矩形．为便于管理，要在中间开辟一横两纵共三条等宽的小道，使种植面积为600平方米，则小道的宽为多少米？若设小道的宽为 $x$ 米，则根据题意，列方程为（）

A、 $35 \times 20 - 35 x - 20 x + 2 x^{2} = 600$ B、 $35 \times 20 - 35 x - 2 \times 20 x = 600$ C、 $(35 - 2 x) (20 - x) = 600$ D、 $(35 - x) (20 - 2 x) = 600$

查看试题解析
12. 目前以 $5 G$ 等为代表的战略性新兴产业蓬勃发展.某市2019年底有 $5 G$ 用户2万户，计划到2021年底全市 $5 G$ 用户数累计达到8.72万户.设全市 $5 G$ 用户数年平均增长率为 $x$ ，则 $x$ 值为（）

A、 $20 %$ B、 $30 %$ C、 $40 %$ D、 $50 %$

查看试题解析

二、填空题

13. 计算 $\sqrt{3} - \sqrt{12} - {(\sqrt{8} - 1)}^{0}$ 的结果是．

查看试题解析
14. 若 $\sqrt{a + 2} + | b - 1 | = 0$ ，则 ${(a + b)}^{2021} =$ ．

查看试题解析
15. 若 $a ， b$ 是方程 $x^{2} + 9 x + 1 = 0$ 的两根，则 $\sqrt{\frac{a}{b}} + \sqrt{\frac{b}{a}}$ =

查看试题解析
16. 《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：直田积八百六十四步，只云阔不及长一十二步．问阔及长各几步？大意是“一个矩形田地的面积等于864平方步，它的宽比长少12步，问长与宽各多少步？”若设矩形田地的宽为x步，则所列方程为．

查看试题解析
17. 已知 $x \neq 0$ ，且 $x^{2} - 3 x y - 4 y^{2} = 0$ ，则 $\frac{y}{x}$ 的值是．

查看试题解析

三、解答题

18. 计算：

(1)、 $(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})^{2}$ ；

(2)、 $\sqrt{{(\frac{1}{3} - \frac{1}{2})}^{2}} + \frac{\sqrt{2}}{2} \times \frac{1}{\sqrt{6}}$ ．

查看试题解析
19. 解方程：

(1)、 $x^{2} - 2 x - 1 = 0$

(2)、 $x^{2} - 5 x + 6 = 0$

查看试题解析
20. 已知关于x的一元二次方程 $x^{2} - (2 k + 1) x + \frac{1}{2} k^{2} - 2 = 0$ .

(1)、求证：无论k为何实数，方程总有两个不相等的实数根；

(2)、若方程的两个实数根 $x_{1}$ ， $x_{2}$ 满足 $x_{1} - x_{2} = 3$ ，求k的值.

查看试题解析
21.

(1)、有一人患了流感，经过两轮传染后，共有121人患了流感，每轮传染中平均每人传染了多少个人？

(2)、在如图的方格中，若要使横，竖，斜对角的3个实数相乘都得到同样的结果，则2个空格的实数之积为多少？
$3 \sqrt{2}$
2
$\sqrt{3}$
1
6

3
$\sqrt{2}$

查看试题解析
22. 已知：关于x的一元二次方程 $x^{2} + \sqrt{m} x - 2 = 0$ 有两个实数根.

(1)、求m的取值范围；

(2)、设方程的两根为 $x_{1}$ 、 $x_{2}$ ，且满足 ${(x_{1} - x_{2})}^{2} - 17 = 0$ ，求m的值.

查看试题解析
23.

(1)、设x，y均为实数，且 $y = \frac{\sqrt{x^{2} - 3} + \sqrt{3 - x^{2}}}{\sqrt{1 - x}} + 2$ ，求 $\frac{y}{x} + \frac{x}{y}$ 的值．

(2)、观察下列等式：
① $3 - 2 \sqrt{2} = (\sqrt{2} - 1)^{2}$ ，
② $5 - 2 \sqrt{6} = (\sqrt{3} - \sqrt{2})^{2}$ ，
③ $7 - 2 \sqrt{12} = (\sqrt{4} - \sqrt{3})^{2}$ ，
…
请你根据以上规律，直接写出第6个等式．

查看试题解析
24. 某水果商店销售一种进价为40元/千克的优质水果，若售价为50元/千克，则一个月可售出500千克；若售价在50元/千克的基础上每涨价1元，则月销售量就减少10千克.

(1)、当售价为55元/千克时，每月销售水果多少千克？

(2)、当月利润为8750元时，每下克水果售价为多少元？

查看试题解析

$3 \sqrt{2}$	2	$\sqrt{3}$
1		6
	3	$\sqrt{2}$