山东省烟台市蓬莱区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-29 类型:期中考试
一、单选题
-
1. 当a为实数时,下列各式中是二次根式的是( )个
, , , , ,
A、3个 B、4个 C、5个 D、6个2. 使式子有意义的实数x的取值范围是( )A、x≤3 B、x≤3且x≠0 C、x<3 D、x<3且x≠03. 若关于x的一元二次方程有实数根,则a的取值范围为( )A、 B、 C、且 D、且4. 如图,四边形 是菱形,E、F分别是 、 两边上的点,不能保证 和 一定全等的条件是( )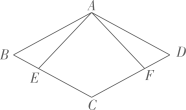 A、 B、 C、 D、5. 下列各式是最简二次根式的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、方程是关于x的一元二次方程 B、方程的常数项是4 C、若一元二次方程的常数项为0,则0必是它的一个根 D、用配方法解一元二次方程 , 可化为7. 下列等式成立的是( )A、 B、 C、 D、8. 如下图,在菱形中, , , 过点D作 , 交的延长线于点E,则线段的长为( )
A、 B、 C、 D、5. 下列各式是最简二次根式的是( )A、 B、 C、 D、6. 下列说法正确的是( )A、方程是关于x的一元二次方程 B、方程的常数项是4 C、若一元二次方程的常数项为0,则0必是它的一个根 D、用配方法解一元二次方程 , 可化为7. 下列等式成立的是( )A、 B、 C、 D、8. 如下图,在菱形中, , , 过点D作 , 交的延长线于点E,则线段的长为( )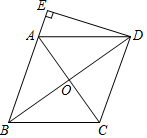 A、 B、 C、 D、9. 已知m、n是方程的两个实数根,则的值为( )A、 B、 C、 D、10. 如下图,在正方形中, , 点E在边上,且 , 点P是对角线上的一个动点,则的最小值为( )
A、 B、 C、 D、9. 已知m、n是方程的两个实数根,则的值为( )A、 B、 C、 D、10. 如下图,在正方形中, , 点E在边上,且 , 点P是对角线上的一个动点,则的最小值为( )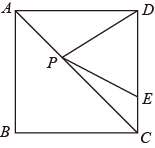 A、 B、 C、 D、11. 在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场,设有x个队参赛,根据题意,可列方程为( )A、 B、 C、 D、12. 如图,在矩形 中, , ,过对角线交点 作 交 于点 ,交 于点 ,则 的长是( )
A、 B、 C、 D、11. 在某篮球邀请赛中,参赛的每两个队之间都要比赛一场,共比赛36场,设有x个队参赛,根据题意,可列方程为( )A、 B、 C、 D、12. 如图,在矩形 中, , ,过对角线交点 作 交 于点 ,交 于点 ,则 的长是( ) A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
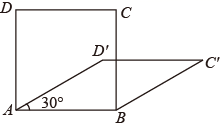
13. 若关于x的一元二次方程的一个根是0,则k的值是 .14. 若 , 则的值是 .15. 对于实数 ,定义运算“◎”如下: ◎ .若 ◎ ,则 .16. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形 的内角,正方形 变为菱形 ,若 ,则菱形 的面积与正方形 的面积之比为 .
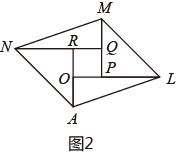
 17. 若 , 则的值为 .18. 如图1,分别沿长方形纸片和正方形纸片的对角线、剪开,拼成如图2所示的 , 若中间空白部分四边形恰好是正方形,且的面积为 , 则正方形的面积为 .
17. 若 , 则的值为 .18. 如图1,分别沿长方形纸片和正方形纸片的对角线、剪开,拼成如图2所示的 , 若中间空白部分四边形恰好是正方形,且的面积为 , 则正方形的面积为 .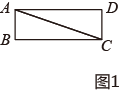
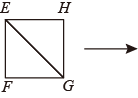
三、解答题
-
19. 计算:(1)、(2)、20. 解方程:(1)、(2)、21. 如图,菱形 的对角线 , 相交于点 , 是 的中点,点 、 在 上, , .
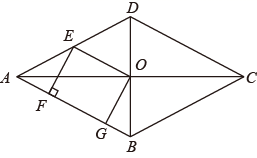 (1)、求证:四边形 是矩形;(2)、若 , ,求 和 的长.22. 求 的值.
(1)、求证:四边形 是矩形;(2)、若 , ,求 和 的长.22. 求 的值.解:设x= ,两边平方得: ,即 ,x2=10
∴x= .
∵ >0,∴ = .
请利用上述方法,求 的值.
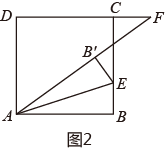
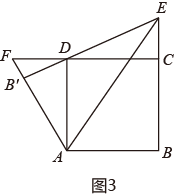
23. 已知关于x的方程 有两实数根.(1)、求k的取值范围;(2)、设方程两实数根分别为 、 ,且 ,求实数k的值.24. 某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)、从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?(2)、在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天补助5元,按租房400天计算,试求今年该地至少有多少户享受到优先搬迁租房奖励?25. 如图,四边形是正方形,点E在直线上,连接将沿所在直线折叠,点B的对应点是点 , 连接并延长直线于点F.(1)、当点F与点C重合时,如图1,试证明:;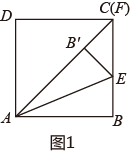 (2)、当点F在的延长线上时,如图2,当点F在的延长线上时,如图3,线段、、有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.
(2)、当点F在的延长线上时,如图2,当点F在的延长线上时,如图3,线段、、有怎样的数量关系?请直接写出你的猜想,并选择一种情况给予证明.