山东省日照市2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列函数中，一次函数是（）

A、 $y = \frac{2}{x} - 1$ B、 $y = x^{2} + 3$ C、 $y = 3 x$ D、 $y = k x + b$ （k、b是常数）

查看试题解析
2. 正方形具有而菱形不具有的性质是（）

A、对角线互相平分 B、每一条对角线平分一组对角 C、对角线相等 D、对边相等

查看试题解析
3. Rt△ABC中，斜边BC=2，则AB²+AC²+BC²的值为（　　）

A、8 B、4 C、6 D、无法计算

查看试题解析
4. 已知一次函数 $y = (3 - m) x^{| m | - 3} + 3$ 的图象上有两点 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，当 $x_{1} < x_{2}$ 时， $y_{1} > y_{2}$ ，则m的值为（）

A、-3 B、-4 C、4 D、4或-4

查看试题解析
5. 若顺次连接四边形ABCD各边中点所得四边形是矩形，则四边形ABCD必然是（　　）

A、菱形 B、对角线相互垂直的四边形 C、正方形 D、对角线相等的四边形

查看试题解析
6. 如图，是一段楼梯，高BC是1.5m，斜边AC是2.5m，如果在楼梯上铺地毯，那么至少需要地毯（）

A、2.5m B、3m C、3.5m D、4m

查看试题解析
7. 如图，在▱ABCD中，AD=6，AB=4，DE平分∠ADC交BC于点E，则BE的长是（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，▱ABCD的对角线AC与BD相交于点O，AB⊥AC.若AB＝4，AC＝6，则BD的长是（）

A、8 B、9 C、10 D、11

查看试题解析
9. 一次函数 $y = k x + b$ 的图象经过 $A (- 1 ， 1)$ ， $B (4 ， 0)$ 两点，若点 $M (2 ， y_{1})$ 和点 $N (3 ， y_{2})$ 恰好也是该函数图象上的两点，则 $y_{1}$ ， $y_{2}$ 的关系是（）

A、 $y_{1} < y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} > y_{2}$ D、无法确定

查看试题解析
10. 一根弹簧原长12 cm，它所挂的重量不超过10 kg，并且挂重1 kg就伸长1.5 cm，写出挂重后弹簧长度y(cm)与挂重x(kg)之间的函数关系式是（）

A、y＝1.5(x＋12)(0≤x≤10) B、y＝1.5x＋12(0≤x≤10) C、y＝1.5x＋12(x≥0) D、y＝1.5(x－12)(0≤x≤10)

查看试题解析
11. 如图，已知AD是三角形纸片ABC的高，将纸片沿直线EF折叠，使点A与点D重合，给出下列判断：
①EF是△ABC的中位线；
②△DEF的周长等于△ABC周长的一半；
③若四边形AEDF是菱形，则AB=AC；
④若∠BAC是直角，则四边形AEDF是矩形，
其中正确的是（）

A、①②③ B、①②④ C、②④ D、①③④

查看试题解析

二、填空题

12. 菱形ABCD的两条对角线长分别为6cm和8cm，则菱形ABCD的面积为；周长为.

查看试题解析
13. 如图，矩形 $A B C D$ 中， $A B = 3$ ， $A D = 1$ ， $A B$ 在数轴上，若以点 $A$ 为圆心，对角线 $A C$ 的长为半径作弧交数轴与点 $M$ ，则点 $M$ 表示的数为.

查看试题解析
14. 如图，在正方形ABCD的外侧，作等边△ADE，则∠EBD= ．

查看试题解析
15. 如图，一次函数 $y = k x + b$ （k、b为常数，且 $k \neq 0$ ）与正比例函数 $y = a x$ （a为常数，且 $a \neq 0$ ）相交于点P，则不等式 $k x + b \leq a x$ 的解集是．

查看试题解析

三、解答题

16. 计算：

(1)、 $2 \sqrt{12} + 3 \sqrt{1 \frac{1}{3}} - \frac{2}{3} \sqrt{48}$ ；

(2)、 $\sqrt{48} - \sqrt{54} \div 2 + (3 - \sqrt{3}) (1 + \frac{1}{\sqrt{3}})$ ．

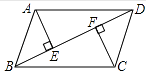
查看试题解析
17. 如图，BD是▱ABCD的对角线，AE⊥BD，CF⊥BD，垂足分别为E、F，求证：AE=CF．

查看试题解析
18. 已知：如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E．

(1)、求证：四边形ADCE为矩形；

(2)、当△ABC满足时（添加一个条件），四边形ADCE是正方形．

查看试题解析
19. 如图1，在平面直角坐标系 $x O y$ 中， $A (a ， 0)$ 、 $B (0 ， b)$ 、 $C (- a ， 0)$ ，且 $\sqrt{a - 2} + b^{2} - 4 b + 4 = 0$ ．

(1)、求证： $∠ A B C = 90 °$ ；

(2)、作 $∠ A B O$ 的平分线交x轴于一点D，求D点的坐标．

查看试题解析
20. 如图，已知一次函数ykxb的图象经过A(2，2)，B（1，4）两点，并且交x轴于点C，交y轴于点D．

(1)、求一次函数的解析式；

(2)、求点C和点D的坐标；

(3)、求△DOB的面积．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ， $∠ B = 90 °$ ， $A B = 8 c m$ ， $A D = 12 c m$ ， $B C = 18 c m$ ，点P从点A出发，以 $1 c m / s$ 的速度向点D运动；点Q从点C同时出发，以 $2 c m / s$ 的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设点P，Q运动的时间为 $t s$ ．

(1)、 $C D$ 边的长度为cm，t的取值范围为．

(2)、从运动开始，当t取何值时， $P Q / / C D$ ？

(3)、从运动开始，当t取何值时， $P Q = C D$ ？

(4)、在整个运动过程中是否存在t值，使得四边形 $P Q C D$ 是菱形？若存在，请求出t值；若不存在，请说明理由．

查看试题解析