山东省临沂市兰山区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-29 类型:期中考试
一、单选题
-
1. 函数中自变量x的取值范围是( )A、x≥0 B、x≠1 C、x≥0且x≠-1 D、x>02. 下列各组数中不能作为直角三角形的三边长的是( )A、2,3,4 B、7,24,25 C、6,8,10 D、9,12,153. 下列根式中能与 合并的是( )A、 B、 C、 D、4. 若▱ABCD的周长为28cm,△ABC的周长为20cm,则AC的长为( )A、8cm B、6cm C、4cm D、3cm5. 如图,▱ABCD的对角线交点是直角坐标系的原点,BC∥x轴,若顶点C坐标是(4,2),BC=7,则顶点D的坐标是( )
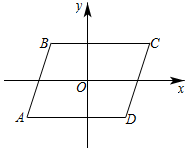 A、(3,-2) B、(-3,2) C、(5,-2) D、(3,-5)6. 如图,在矩形ABCD中,AB=8, , 将矩形沿AC折叠,点D落在点D'处,则重叠部分的面积为( )
A、(3,-2) B、(-3,2) C、(5,-2) D、(3,-5)6. 如图,在矩形ABCD中,AB=8, , 将矩形沿AC折叠,点D落在点D'处,则重叠部分的面积为( ) A、6 B、8 C、10 D、127. 若一个三角形的三边长分别是则此三角形的周长为( )A、 B、 C、 D、8. 已知△ABC中,AB=17,AC=10,BC边上的高AH=8,则BC的长是( )A、21 B、21或6 C、21或9 D、159. 如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边是6,小正方形的边长是2,则大正方形的面积是( )
A、6 B、8 C、10 D、127. 若一个三角形的三边长分别是则此三角形的周长为( )A、 B、 C、 D、8. 已知△ABC中,AB=17,AC=10,BC边上的高AH=8,则BC的长是( )A、21 B、21或6 C、21或9 D、159. 如图,用4个相同的直角三角形与一个小正方形拼成的大正方形,若图中直角三角形较短的直角边是6,小正方形的边长是2,则大正方形的面积是( )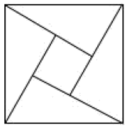 A、121 B、144 C、196 D、10010. 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中有( )个是正确的.
A、121 B、144 C、196 D、10010. 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中有( )个是正确的.①∠DAF=45° ②△ABE≌△ACD ③AD平分∠EDF ④
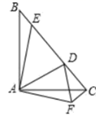 A、4 B、3 C、2 D、111. 如图,在菱形 中,P是对角线 上一动点,过点P作 于点E. 于点F.若菱形 的周长为20,面积为24,则 的值为( )
A、4 B、3 C、2 D、111. 如图,在菱形 中,P是对角线 上一动点,过点P作 于点E. 于点F.若菱形 的周长为20,面积为24,则 的值为( ) A、4 B、 C、6 D、12. 如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离是( )
A、4 B、 C、6 D、12. 如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离是( )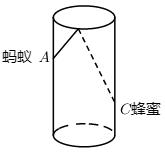 A、15cm B、16cm C、17cm D、18cm
A、15cm B、16cm C、17cm D、18cm二、填空题
-
13. 计算: .14. 计算: .15. 已知等边三角形的边长为2cm,则它的面积为 .16. 三角形一条中位线所截成的新三角形与原三角形周长之和等于30cm,则原三角形周长为 .17. 如图,菱形ABCD中,对角线AC和BD相交于O,已知AC=24,BD=10,则BC边上的高DE等于 .
 18. 如图,正方形ABCD的边长为4,E为BC上的点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为.
18. 如图,正方形ABCD的边长为4,E为BC上的点,BE=1,F为AB的中点,P为AC上一个动点,则PF+PE的最小值为.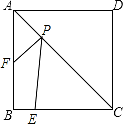
三、解答题
-
19. 计算题:(1)、(2)、20. 已知,如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,如果AB=3cm,BC=5cm,求FC的长.
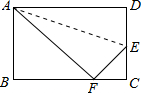 21. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.
21. 如图,在正方形ABCD中,点E,F在AC上,且AF=CE.求证:四边形BEDF是菱形.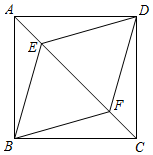 22. 如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH,当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形,并说明理由.
22. 如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH,当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形,并说明理由.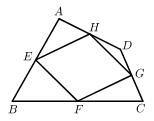 23. 如图,已知一块四边形的草地ABCD,其中∠A=60°,∠B=∠D=90°,AB=10米,CD=6米,求这块草地的面积.(结果保留整数)
23. 如图,已知一块四边形的草地ABCD,其中∠A=60°,∠B=∠D=90°,AB=10米,CD=6米,求这块草地的面积.(结果保留整数)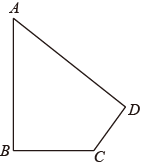 24. 阅读材料,解答问题。
24. 阅读材料,解答问题。例:若代数式 的值是常数2,求a的取值范围.
分析:原式= , 而 表示数a在数轴上的对应点到原点的距离,表示数a在数轴上的对应点到数2的对应点的距离,所以我们可以借助数轴进行分析.
解:原式=在数轴上,分别讨论数a表示的点在数2表示的点左边,在数2表示的点和数4表示的点之间,在数4表示的点右边,可得a的范围应是2≤a≤4.
 (1)、此例题的解答过程用了哪些数学思想?请举例.(2)、化简 .25. 小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形ABCD和平行四边形HEFG(如图1),且BC,EF在一条直线上,点D落在边HE上.经小明测量,发现此时B、D、G三个点在一条直线上,∠F=67.5°,DG=2.
(1)、此例题的解答过程用了哪些数学思想?请举例.(2)、化简 .25. 小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形ABCD和平行四边形HEFG(如图1),且BC,EF在一条直线上,点D落在边HE上.经小明测量,发现此时B、D、G三个点在一条直线上,∠F=67.5°,DG=2.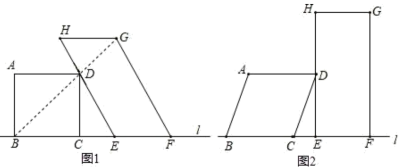 (1)、求HG的长度;(2)、设BC的长度为a,CE=;(用含a的代数式表示)(3)、小明接着探究,在保证BC、EF位置不变的前提条件下,从点A向右推动正方形,知道四边形EFGH刚好变为矩形时停止推动(如图2),若此时 , 求BF的长度.
(1)、求HG的长度;(2)、设BC的长度为a,CE=;(用含a的代数式表示)(3)、小明接着探究,在保证BC、EF位置不变的前提条件下,从点A向右推动正方形,知道四边形EFGH刚好变为矩形时停止推动(如图2),若此时 , 求BF的长度.