山东省聊城市高唐县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-29 类型:期中考试
一、单选题
-
1. 在实数﹣2, , 3.1415926, , ﹣π+1,0.1010010010001中,无理数有( )个A、2 B、3 C、4 D、52. 8的立方根是( )A、2 B、±2 C、±2 D、23. 下列计算正确的是( )A、 B、 C、 D、4. 在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )A、如果∠A-∠B=∠C,那么△ABC是直角三角形 B、如果a2=b2-c2 , 那么△ABC是直角三角形,且∠C=90° C、如果∠A︰∠B︰∠C=1︰3︰2,那么△ABC是直角三角形 D、如果a2︰b2︰c2=9︰16︰25,那么△ABC是直角三角形5. 如图,已知数轴上的点A,B,C,D分别表示数﹣2,1,2,3,则表示3﹣的点P应落在线段( )
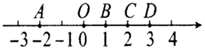 A、AO上 B、OB上 C、BC上 D、CD上6. 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若按照图中所标注的数据,则△ABC的周长是( )
A、AO上 B、OB上 C、BC上 D、CD上6. 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,若按照图中所标注的数据,则△ABC的周长是( )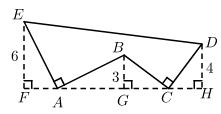 A、15+3 B、15 C、20 D、237. 已知 ,下列式子不一定成立的是( )A、 B、 C、 D、8. 不等式 的解集在数轴上表示为( )A、
A、15+3 B、15 C、20 D、237. 已知 ,下列式子不一定成立的是( )A、 B、 C、 D、8. 不等式 的解集在数轴上表示为( )A、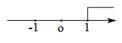 B、
B、 C、
C、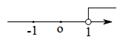 D、
D、 9. 关于x的不等式组 的解集为x<3,那么m的取值范围为( )A、m=3 B、m>3 C、m<3 D、m≥310. 如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A处.若∠DBC=24°,则∠A′EB等于( )
9. 关于x的不等式组 的解集为x<3,那么m的取值范围为( )A、m=3 B、m>3 C、m<3 D、m≥310. 如图,将矩形纸片ABCD沿BE折叠,使点A落在对角线BD上的A处.若∠DBC=24°,则∠A′EB等于( )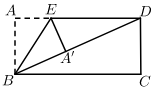 A、66° B、60° C、57° D、48°11. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( )
A、66° B、60° C、57° D、48°11. 如图,在菱形 中,对角线 相交于点 为 中点, .则线段 的长为:( ) A、 B、 C、3 D、512. 如图,F为正方形ABCD的边AD上一点,CE⊥CF交AB的延长线于点E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为( )
A、 B、 C、3 D、512. 如图,F为正方形ABCD的边AD上一点,CE⊥CF交AB的延长线于点E,若正方形ABCD的面积为64,△CEF的面积为50,则△CBE的面积为( )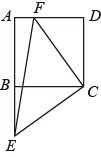 A、20 B、24 C、25 D、26
A、20 B、24 C、25 D、26二、填空题
-
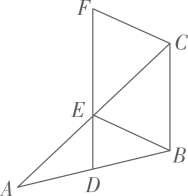
13. 的算术平方根是14. 若 ,则 .15. 如图所示,点D、E分别是 的边AB、AC的中点,连接BE,过点C做 ,交DE的延长线于点F,若 ,则DE的长为 .
 16. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为 .
16. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为 .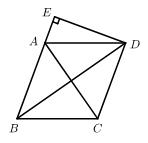 17. 对于实数a,b,我们定义符号min{a,b}的意义为:当a<b时,min{a,b}=a;当a≥b时,min{a,b}=b,如:min{4,﹣2}=﹣2,min{5,5}=5,根据上面的材料回答下列问题:若时,则x的取值范围是
17. 对于实数a,b,我们定义符号min{a,b}的意义为:当a<b时,min{a,b}=a;当a≥b时,min{a,b}=b,如:min{4,﹣2}=﹣2,min{5,5}=5,根据上面的材料回答下列问题:若时,则x的取值范围是三、解答题
-
18. 计算(1)、(2)、19. 解不等式(组)(1)、解不等式 , 并在数轴上表示其解集.
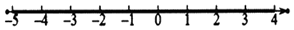 (2)、解不等式组20. 如图,在 的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(2)、解不等式组20. 如图,在 的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.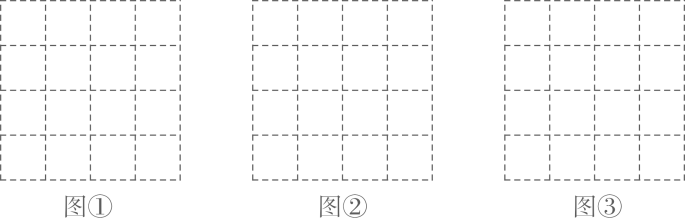 (1)、在图①中,画一个直角三角形,使它的三边长都是有理数;(2)、在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;(3)、在图③中,画一个直角三角形,使它的三边长都是无理数.21. 阅读理解.
(1)、在图①中,画一个直角三角形,使它的三边长都是有理数;(2)、在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;(3)、在图③中,画一个直角三角形,使它的三边长都是无理数.21. 阅读理解.∵ < < ,即2< <3.
∴1< ﹣1<2
∴ ﹣1的整数部分为1,
∴ ﹣1的小数部分为 ﹣2.
解决问题:已知a是 ﹣3的整数部分,b是 ﹣3的小数部分.
(1)、求a,b的值;(2)、求(﹣a)3+(b+4)2的平方根,提示:( )2=17.22. 在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)、求每台电脑、每台电子白板各多少万元?(2)、根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.23. 如图, 的对角线AC,BD相交于点O,过点O作 ,分别交AB,DC于点E、F,连接AF、CE. (1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.24. 如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.
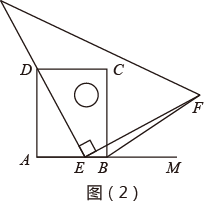
(1)、若 ,求EF的长;(2)、判断四边形AECF的形状,并说明理由.24. 如图,矩形ABCD中,E是AD的中点,延长CE、BA交于点F,连接AC、DF.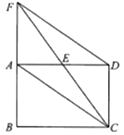 (1)、求证:四边形ACDF是平行四边形;(2)、当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.25. 如图(1)(2),四边形ABCD是正方形,M是AB延长线上的一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.
(1)、求证:四边形ACDF是平行四边形;(2)、当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.25. 如图(1)(2),四边形ABCD是正方形,M是AB延长线上的一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.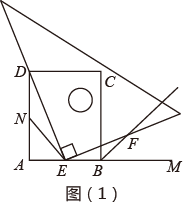
 (1)、如图(1),当点E在AB边的中点位置时;
(1)、如图(1),当点E在AB边的中点位置时;①猜想DE与EF满足的数量关系是 ;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是 ;
③请证明上述的两个猜想.
(2)、如图(2),当点E在AB边上的任意位置时,请你在AD边上找一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系.