山东省德州市禹城市2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-29 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$ C、 $3 \sqrt{2} - 2 \sqrt{2} = 1$ D、 $\sqrt{2} \div \sqrt{\frac{1}{2}} = 2$

查看试题解析
2. 下列各组数是三角形的三边长，不能组成直角三角形的一组数是（）

A、5， 12， 13 B、1， 2， $\sqrt{3}$ C、 $\sqrt{3} ， \sqrt{4} ， \sqrt{5}$ D、6，8， 10

查看试题解析
3. 下列式子正确的是（）

A、 $\sqrt{(- 5)^{2}} = - 5$ B、 $\sqrt{(- 5)^{2}} = 5$ C、 $\sqrt{(- 5)^{2}} = \pm 5$ D、 $\sqrt{(\pm 5)^{2}} = \pm 5$

查看试题解析
4. 下列定理中逆定理正确的个数是（）
①对角线互相平分的四边形是平行四边形；
②在直角三角形中，斜边的平方等于两直角边的平方和；
③角平分线上的点到这个角两边的距离相等；
④矩形的对角线相等．

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 将面积为 $2 π$ 的半圆与两个正方形A和正方形B拼接如图所示，这两个正方形面积的和为（）

A、 $4 π$ B、8 C、 $2 π$ D、16

查看试题解析
6. 菱形的两条对角线长分别是6和8，则此菱形的高是（）

A、2.4 B、 $\frac{24}{5}$ C、10 D、16

查看试题解析
7. 如图，数轴上点A所表示的数是（　　）

A、 $\sqrt{5}$ B、﹣ $\sqrt{5}$ +1 C、 $\sqrt{5}$ +1 D、 $\sqrt{5}$ ﹣1

查看试题解析
8. 如图，一个工人拿一个2.5米长的梯子，底端A放在距离墙根C点0.7米处，另一头B点靠墙，如果梯子的顶部下滑0.4米，梯子的底部向外滑（）米.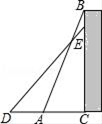

A、0.4 B、0.6 C、0.7 D、0.8

查看试题解析
9. 中外数学家曾经针对已知三角形的三边，求其面积问题进行过深入研究，古希腊几何学家海伦给出“海伦公式”： $s = \sqrt{p (p - a) (p - b) (p - c)}$ ，其中 $p = \frac{a + b + c}{2}$ ；我国南宋数学家秦九韶给出“秦九韶公式” $s = \frac{1}{2} \sqrt{a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}}$ ，若一个三角形的三边长分别为2，3，4，则其面积是（）

A、 $\frac{\sqrt{15}}{2}$ B、 $\frac{3 \sqrt{15}}{4}$ C、 $\frac{3 \sqrt{15}}{2}$ D、 $\frac{3 \sqrt{15}}{8}$

查看试题解析
10. 如图，E是 $▱ A B C D$ 边 $A D$ 延长线上一点，连接 $B E$ ， $C E$ ， $B D$ ， $B E$ 交 $C D$ 于点F．添加以下条件，不能判定四边形 $B C E D$ 为平行四边形的是（）

A、 $∠ A B D = ∠ D C E$ B、 $D F = C F$ C、 $∠ A E B = ∠ B C D$ D、 $∠ A E C = ∠ C B D$

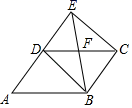查看试题解析
11. 如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（）

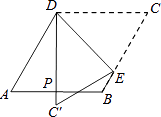A、78° B、75° C、60° D、45°

查看试题解析
12. 如图，圆柱形玻璃杯，高为12cm，底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的A处，则蚂蚁到达蜂蜜的最短距离（　　）cm．

A、14 B、15 C、16 D、17

查看试题解析

二、填空题

13. 若式子 $\frac{\sqrt{x + 1}}{x}$ 有意义，则x的取值范围是

查看试题解析
14. 公元3世纪，我国数学家刘徽就能利用近似公式 $\sqrt{a^{2} + r} \approx a + \frac{r}{2 a}$ 得到根式的近似值，利用此公式得到 $\sqrt{5}$ 的近似值，则可知 $\sqrt{5} = \sqrt{2^{2} + 1}$ $\approx$ ．

查看试题解析
15. 《九章算术》中有一道题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何？”大致意思是：一根竹子高1丈，折断后竹子顶端落在离竹子底端3尺处，那么折断处离地面的高度为尺．（1丈=10尺）

查看试题解析
16. 在探索数学名题“尺规三等分角”的过程中，有下面的问题：如图BD是平行四边形ABCD的对角线，点E在BD上，DC＝DE＝AE，∠1＝25°，则∠C的大小是.

查看试题解析
17. 把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为．

查看试题解析
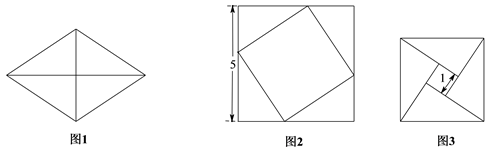18. 长为1，宽为a的矩形纸片（ $\frac{1}{2} < a < 1$ ），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n次操作后，剩下的矩形为正方形，则操作终止．当n=3时，a的值为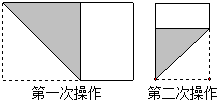

查看试题解析

三、解答题

19.

(1)、 $\sqrt{27} - \frac{1}{3} \sqrt{18} - \sqrt{12}$

(2)、 $(\sqrt{5} - \sqrt{3})^{2} - (\sqrt{5} + 2) (\sqrt{5} - 2)$

查看试题解析
20. 如图， $R t Δ A B C$ 中， $∠ B = 90 °$ ， $A B = 3$ ， $B C = 4$ ， $C D = 12$ ， $A D = 13$ ，点E是AD的中点，求CE的长.

查看试题解析
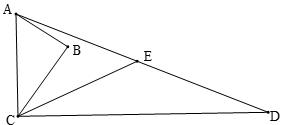21. 如图，已知∠AOB，OA＝OB，点E在边OB上，四边形AEBF是平行四边形．

(1)、请你只用无刻度的直尺在图中画出∠AOB的平分线．（保留作图痕迹，不写作法）

(2)、请说明你的画法的正确性．

查看试题解析
22. 如图，在△ABC中，∠ACB=90°，D，E分别为AC，AB的中点，BF∥CE交DE的延长线于点F．

(1)、求证：四边形ECBF是平行四边形；

(2)、当∠A=30°时，求证：四边形ECBF是菱形．

查看试题解析
23. 阅读材料：规定初中考试不能使用计算器后，小明是这样解决问题的：
已 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值．他是这样分析的：先将a化简， $a = \frac{1}{2 + \sqrt{3}} =$ $\frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ，然后将其代入求值，请你根据小明的分析过程，解决如下问题：

(1)、若 $a = \frac{1}{\sqrt{2} - 1}$ ，求出 $4 a^{2} - 8 a + 1$ 的值．

(2)、使用以上方法化简： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} +$ $\frac{1}{\sqrt{7} + \sqrt{5}} + ⋯ + \frac{1}{\sqrt{289} + \sqrt{287}}$ ．

查看试题解析
24. 【发现与证明】
如图，正方形 $A B C D$ 的对角线相交于点O，点O是正方形 $A^{'} B^{'} C^{'} O$ 的一个顶点，如果两个正方形的边长都等于a，那么正方形 $A^{'} B^{'} C^{'} O$ 绕点O无论怎样转动，两个正方形重叠部分的面积是一个定值．

(1)、请你写出这个定值，并证明你的结论．

(2)、【应用迁移】
如图，四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = ∠ B C D = 9 0^{∘}$ ，连接 $A C$ ．若 $A C = 8$ ，求四边形 $A B C D$ 的面积．

查看试题解析
25. 如图，在四边形ABCD中，AB∥CD，∠ADC＝90°，AD＝12cm，AB＝18cm，CD＝23cm，动点P从点A出发，以1cm/s的速度向点B运动，同时动点Q从点C出发，以2cm/s的速度向点D运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为t秒．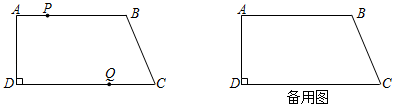

(1)、当t＝3时，PB＝cm．

(2)、当t为何值时，直线PQ把四边形ABCD分成两个部分，且其中的一部分是平行四边形？

(3)、四边形PBQD能否成为菱形？若能，求出t的值；若不能，请说明理由．

查看试题解析