山东省德州市庆云县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-29 类型:期中考试
一、单选题
-
1. 下列各式属于最简二次根式的是( )
A、 B、 C、 D、2. 若式子在实数范围内有意义,则m的取值范围是( )A、 B、且 C、且 D、3. 已知且 , 化简二次根式的符合题意结果是( )A、 B、 C、 D、4. 下列命题:①如果a、b、c为一组勾股数,那么4a、4b、4c仍是勾股数;
②如果直角三角形的两边是3,4,那么斜边必是5;
③如果一个三角形的三边是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2:b2:c2=2:1:1.
其中正确的是( )
A、①② B、①③ C、①④ D、②④5. 如图,在平行四边形中,E,F是对角线上不同的两点,连接 , , , .下列条件中,不能得出四边形一定是平行四边形的为( ) A、 B、 C、 D、6. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
A、 B、 C、 D、6. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )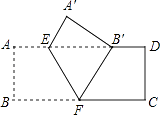 A、12 B、24 C、12 D、167. 如图,在Rt△ABC中,AC=6,BC=8,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F.则线段EF的最小值为( )
A、12 B、24 C、12 D、167. 如图,在Rt△ABC中,AC=6,BC=8,D为斜边AB上一动点,DE⊥BC,DF⊥AC,垂足分别为E、F.则线段EF的最小值为( ) A、6 B、 C、5 D、8. 如图,菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE,若∠BCD=50°,则∠OED的度数是( )
A、6 B、 C、5 D、8. 如图,菱形ABCD中,AC交BD于点O,DE⊥BC于点E,连接OE,若∠BCD=50°,则∠OED的度数是( ) A、35° B、30° C、25° D、20°9. 如图,平行四边形中,对角线相交于O, , 分别是的中点,以下结论:①;②;③;④平分 , 其中正确的是( )
A、35° B、30° C、25° D、20°9. 如图,平行四边形中,对角线相交于O, , 分别是的中点,以下结论:①;②;③;④平分 , 其中正确的是( ) A、①②③ B、①③④ C、①②④ D、②③④10. 如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结 若 , ,则 的度数为( )
A、①②③ B、①③④ C、①②④ D、②③④10. 如图,在▱ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连结 若 , ,则 的度数为( )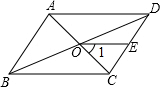 A、 B、 C、 D、11. 如图,在正方形 中,E为 边上一点,F为 延长线上一点,且 ,连接 .给出下列至个结论:① ;② ;③ ;④ ;⑤ .其中正确结论的个数是( )
A、 B、 C、 D、11. 如图,在正方形 中,E为 边上一点,F为 延长线上一点,且 ,连接 .给出下列至个结论:① ;② ;③ ;④ ;⑤ .其中正确结论的个数是( ) A、 B、 C、 D、12. 边长为1的等边 , 分别取 , 边的中点D,E,连接 , 作得到四边形 , 它的周长记作;分别取 , 的中点 , , 连接 , 作 , 得到四边形 , 它的周长记作照此规律作下去,则等于( )
A、 B、 C、 D、12. 边长为1的等边 , 分别取 , 边的中点D,E,连接 , 作得到四边形 , 它的周长记作;分别取 , 的中点 , , 连接 , 作 , 得到四边形 , 它的周长记作照此规律作下去,则等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若最简二次根式与可以合并,则a的值为 .14. 已知,x、y是有理数,且y=+ ﹣4,则2x+3y的立方根为 .15. 如图,已知 , 数轴上点A所表示的数是 .
 16. 如图,点O是菱形对角线的交点, , 连接 , 设 , 则的长为 .
16. 如图,点O是菱形对角线的交点, , 连接 , 设 , 则的长为 .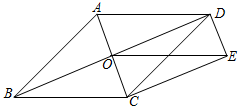 17. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a、b,那么(a+b)2的值是
17. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a、b,那么(a+b)2的值是 18. 如图,四边形ABCD中, , , , 点P自点A向D以1cm/s的速度运动,到D点即停止;点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ分原四边形为两个新四边形;则当P,Q同时出发秒后其中一个新四边形为平行四边形.
18. 如图,四边形ABCD中, , , , 点P自点A向D以1cm/s的速度运动,到D点即停止;点Q自点C向B以2cm/s的速度运动,到B点即停止,直线PQ分原四边形为两个新四边形;则当P,Q同时出发秒后其中一个新四边形为平行四边形.
三、解答题
-
19.(1)、(2)、20. 先化简,再求值: .其中 .21.(1)、如图,在四边形 中, , , , , , 求证: .
 (2)、如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,6 秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号).
(2)、如图,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为13米,此人以0.5米每秒的速度收绳,6 秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号). 22. 如图,在中,对角线与相交于点O,点E,F分别在和的延长线上,且 , 连接 , .
22. 如图,在中,对角线与相交于点O,点E,F分别在和的延长线上,且 , 连接 , . (1)、求证:≌;(2)、连接 , , 当平分时,四边形是什么特殊四边形?请说明理由.23. 如图,中, , 是边上的高,点O是中点,延长到E,使 , 连接 , .
(1)、求证:≌;(2)、连接 , , 当平分时,四边形是什么特殊四边形?请说明理由.23. 如图,中, , 是边上的高,点O是中点,延长到E,使 , 连接 , .
求证:四边形是矩形.
24. 如图所示,在中, , 点D从点C出发沿方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点达到终点时,另一个点也随之停止运动.设点运动的时间为t秒().过点作于点F,连接 . (1)、求证:;(2)、四边形可能成为菱形吗?如果可能,求出相应的t值;如果不可能,说明理由.25. 如图一,四边形是正方形,点E是边的中点, , 且交正方形外角的平分线于点F.
(1)、求证:;(2)、四边形可能成为菱形吗?如果可能,求出相应的t值;如果不可能,说明理由.25. 如图一,四边形是正方形,点E是边的中点, , 且交正方形外角的平分线于点F. (1)、求证:(提示:取的中点G,连接).(2)、如图二所示,若把条件“点E是边的中点”改为“点E为上任意一点”,其他条件不变,那么结论是否成立呢?若成立,请你证明,若不成立,请说明理由.(3)、如图三所示,若把条件“点E是边的中点”改为“点E为延长线上任意一点”,其他条件不变,那么结论是否成立呢?若成立,请你证明,若不成立,请说明理由.
(1)、求证:(提示:取的中点G,连接).(2)、如图二所示,若把条件“点E是边的中点”改为“点E为上任意一点”,其他条件不变,那么结论是否成立呢?若成立,请你证明,若不成立,请说明理由.(3)、如图三所示,若把条件“点E是边的中点”改为“点E为延长线上任意一点”,其他条件不变,那么结论是否成立呢?若成立,请你证明,若不成立,请说明理由.