北师大版备考2022中考数学二轮复习专题7 分式方程
试卷更新日期:2022-03-29 类型:二轮复习
一、单选题
-
1. 关于的分式方程的解为正数,则的取值范围是( )A、 B、 C、且 D、且2. 在2020年3月底新过师炎疫情在我国得到快速控制,教育部要求低风险区错时、错峰开学,某校在只有初三年级开学时,一段时间用掉120瓶消毒液,在初二、初一年级也错时、错峰开学后,平均每天比原来多用4瓶消毒液,这样120瓶消毒液比原来少用5天,若设原来平均每天用掉x瓶消毒液,则可列方程是( )A、 B、 C、 D、3. 若关于 的不等式组 无解,且关于 的分式方程 的解为非负整数,则符合条件的所有整数 的和为( )A、6 B、16 C、18 D、204. 若整数a使关于x的不等式组 无解,且使关于x的分式方程 有整数解,那么所有满足条件的a的值的积是( )A、2 B、3 C、 D、85. 如果 是二次根式,那么 x 应适合的条件是( )
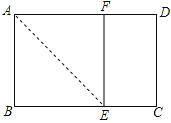
A、x ≥3 B、x ≤3 C、x >3 D、x <36. 已知公式 ( ),则表示 的公式是( )A、 B、 C、 D、7. 若关于x的方程 的解为负数,且关于x的不等式组 无解,则所有满足条件的整数a的值之和是( )A、5 B、7 C、9 D、108. 若 + = ,则 + 的值为( )A、0 B、1 C、﹣1 D、无法计算9. 若关于x的不等式组 有且只有三个整数解,且关于x的分式方程 ﹣ =﹣1有整数解,则满足条件的整数a的值为( )A、15 B、3 C、﹣1 D、﹣1510.已知矩形ABCD中,AB=1,在BC上取一点E , 沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD=( ).
 A、 B、
A、 B、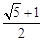 C、
D、2
C、
D、2
二、填空题
-
11. 当x=时, 与 互为相反数.12. 用换元法解方程 时,如果设 ,那么原方程化成关于 的整式方程是13. 若关于x的方程 有增根,则增根 .14. 已知a>b>0,且 ,则 。
15. 如图,在平面直角坐标系中,有一宽度为1的长方形纸带,平行于y轴,在x轴的正半轴上移动,交x轴的正半轴于点A、D , 两边分别交函数y1= (x>0)与y2= (x>0)的图像于B、F和E、C , 若四边形ABCD是矩形,则A点的坐标为 .
(x>0)与y2= (x>0)的图像于B、F和E、C , 若四边形ABCD是矩形,则A点的坐标为 . 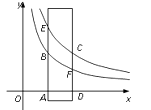 16. 如图,甲,乙两人分别从A、B两地同时出发去往C地,在距离C地2500米处甲追上乙;若乙提前10分钟出发,则在距离C地1000米处甲追上乙。已知,乙每分钟走60米,那么甲的速度是每分钟米。
16. 如图,甲,乙两人分别从A、B两地同时出发去往C地,在距离C地2500米处甲追上乙;若乙提前10分钟出发,则在距离C地1000米处甲追上乙。已知,乙每分钟走60米,那么甲的速度是每分钟米。 17. 随着5月底广州“新冠”疫情的爆发,为了抵抗病毒的侵袭,量子巴川中学组织教师到社区卫生服务中心接种新冠病毒疫苗,由于疫苗数量有限,所以要分批进行接种.初中三个年级都有教师参加第一批疫苗接种,其中初一年级,初二年级和初三年级参加第一批疫苗接种的教师人数之比是5:3:2,第二批疫苗到货后,初中三个年级都有教师参加第二批疫苗接种,初三年级新增接种教师人数占总新增接种教师人数的 ,第二批疫苗接种后初三年级接种教师总人数占这三个年级接种教师总人数之和的 ,并且初一年级接种教师总人数和初二年级接种教师总人数之比为 ,则初二年级第二批接种教师人数与初中三个年级接种教师总人数之比为.18. 观察下列等式:
17. 随着5月底广州“新冠”疫情的爆发,为了抵抗病毒的侵袭,量子巴川中学组织教师到社区卫生服务中心接种新冠病毒疫苗,由于疫苗数量有限,所以要分批进行接种.初中三个年级都有教师参加第一批疫苗接种,其中初一年级,初二年级和初三年级参加第一批疫苗接种的教师人数之比是5:3:2,第二批疫苗到货后,初中三个年级都有教师参加第二批疫苗接种,初三年级新增接种教师人数占总新增接种教师人数的 ,第二批疫苗接种后初三年级接种教师总人数占这三个年级接种教师总人数之和的 ,并且初一年级接种教师总人数和初二年级接种教师总人数之比为 ,则初二年级第二批接种教师人数与初中三个年级接种教师总人数之比为.18. 观察下列等式:, ,
将以上三个等式两边分别相加得: = + + = =
猜想并得出: =
根据以上推理,求出分式方程 的解是 .
三、计算题(共20分)
-
19. 计算(1)、(2)、已知 .求代数式 的值.(3)、先化简,再求值 ,其中m=(4)、解分式方程: +3.
四、作图题(共11分)
-
20. 小明根据学习函数的经验,对函数y=x+ 的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
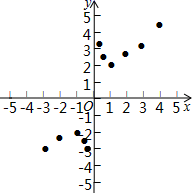 (1)、函数y=x+ 的自变量x的取值范围是.(2)、如表列出了y与x的几组对应值,请写出m,n的值:m= , n=.(3)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.(4)、结合函数的图象,请完成:
(1)、函数y=x+ 的自变量x的取值范围是.(2)、如表列出了y与x的几组对应值,请写出m,n的值:m= , n=.(3)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象.(4)、结合函数的图象,请完成:①当y= 时,x=;
②写出该函数的一条性质;
③若方程x+ =t有两个相等的实数根,则t的值是.
x
…
﹣3
﹣2
﹣1
1
2
3
4
…
y
…
﹣2
m
2
n
…
五、解答题(共43分)
-
21. 在实数范围内只有一个实数是关于x的方程 的根,求实数k的所有可能值.22. 如果方程 与 的解相同,求(a-3)2的值.23. 某市公交快速通道开通后,为响应市政府“绿色出行”的号召,家住新城的小王上班由自驾车改为乘坐公交车.已知小王家距上班地点18千米,他用乘公交车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程的2倍还多9千米,他从家出发到达上班地点,乘公交车方式所用时间是自驾车方式所用时间的 .小王用自驾车方式上班平均每小时行驶多少千米?24. 为配合“一带一路”国家倡议,某铁路货运集装箱物流园区正式启动了2期扩建工程.一项地基基础加固处理工程由A、B两个工程公司承担建设,已知A工程公司单独建设完成此项工程需要180天,A工程公司单独施工45天后,B工程公司参与合作,两工程公司又共同施工54天后完成了此项工程.(1)、求B工程公司单独建设完成此项工程需要多少天?(2)、由于受工程建设工期的限制,物流园区管委会决定将此项工程划包成两部分,要求两工程公司同时开工,A工程公司建设其中一部分用了m天完成,B工程公司建设另一部分用了n天完成,其中m,n均为正整数,且m<46,n<92,求A、B两个工程公司各施工建设了多少天?25. 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC, .E是边AB的中点,联结DE、CE,且DE⊥CE.设AD=x,BC=y.
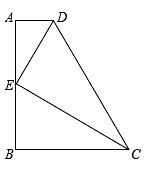 (1)、如果∠BCD=60°,求CD的长;(2)、求y关于x的函数解析式,并写出自变量x的取值范围;(3)、联结BD.如果△BCD是以边CD为腰的等腰三角形,求x的值.
(1)、如果∠BCD=60°,求CD的长;(2)、求y关于x的函数解析式,并写出自变量x的取值范围;(3)、联结BD.如果△BCD是以边CD为腰的等腰三角形,求x的值.
-
-