北师大版备考2022中考数学二轮复习专题6 一元二次方程

试卷更新日期：2022-03-29 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 文博会期间，某公司调查一种工艺品的销售情况，下面是两位调查员和经理的对话．
小张：该工艺品的进价是每个22元；
小李：当销售价为每个38元时，每天可售出160个；当销售价降低3元时，平均每天将能多售出120个．
经理：为了实现平均每天3640元的销售利润，这种工艺品的销售价应降低多少元？
设这种工艺品的销售价每个应降低x元，由题意可列方程为（）

A、（38﹣x）（160+ $\frac{x}{3}$ ×120）＝3640 B、（38﹣x﹣22）（160+120x）＝3640 C、（38﹣x﹣22）（160+3x×120）＝3640 D、（38﹣x﹣22）（160+ $\frac{x}{3}$ ×120）＝3640

查看试题解析
2. 若关于x的一元二次方程ax²﹣4x＋2＝0有两个实数根，则a的取值范围是（）

A、a≤2 B、a≤2且a≠0 C、a＜2 D、a＜2且a≠0

查看试题解析
3. 抛物线 $y = a x^{2} + b x + c$ （a，b，c为常数）开口向下且过点 $A (1 ， 0)$ ， $B (m ， 0)$ （ $- 2 < m < - 1$ ），下列结论：① $2 b + c > 0$ ；② $2 a + c < 0$ ；③ $a (m + 1) - b + c > 0$ ；④若方程 $a (x - m) (x - 1) - 1 = 0$ 有两个不相等的实数根，则 $4 a c - b^{2} < 4 a$ .其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
4. 已知x=m是一元二次方程x²+2x+n-3=0的一个根，则m+n的最大值等于（）

A、 $\frac{13}{4}$ B、4 C、 $- \frac{15}{4}$ D、 $- \frac{13}{4}$

查看试题解析
5. 对于一个函数，自变量x取c时，函数值 $y$ 等于0，则称c为这个函数的零点．若关于x的二次函数 $y = - x^{2} - 10 x + m$ $(m \neq 0)$ 有两个不相等的零点 $x_{1}, x_{2} (x_{1} < x_{2})$ ，关于x的方程 $x^{2} + 10 x - m - 2 = 0$ 有两个不相等的非零实数根 $x_{3}, x_{4} (x_{3} < x_{4})$ ，则下列关系式一定正确的是（）

A、 $0 < \frac{x_{1}}{x_{3}} < 1$ B、 $\frac{x_{1}}{x_{3}} > 1$ C、 $0 < \frac{x_{2}}{x_{4}} < 1$ D、 $\frac{x_{2}}{x_{4}} > 1$

查看试题解析
6. 如图，二次函数y＝ax²+bx+c的图象与x轴相交于A，B两点，C(m，﹣3)是图象上的一点，且AC⊥BC，则a的值为（）

A、2 B、 $\frac{1}{2}$ C、3 D、 $\frac{1}{3}$

查看试题解析
7. 对于两个不相等的实数 $a ， b$ ，我们规定符号 $max {a ， b}$ 表示 $a ， b$ 中较大的数，如 $\max {2 ， 4} = 4$ ，按这个规定，方程 $\max {x ， - x} = \frac{2 x + 1}{x}$ 的解为（）

A、 $1 - \sqrt{2}$ B、 $2 - \sqrt{2}$ C、 $1 - \sqrt{2} 或 1 + \sqrt{2}$ D、 $1 + \sqrt{2}$ 或-1

查看试题解析
8. 欧几里得是古希腊数学家，所著的《几何原本》闻名于世．在《几何原本》中，形如x²+ax＝b²的方程的图解法是：如图，以 $\frac{a}{2}$ 和b为直角边作Rt△ABC，再在斜边上截取BD＝ $\frac{a}{2}$ ，则图中哪条线段的长是方程x²+ax＝b²的解？答：是（）

A、AC B、AD C、AB D、BC

查看试题解析
9. 如图，△ABC是一块锐角三角形材料，高线AH长8 cm，底边BC长10 cm，要把它加工成一个矩形零件，使矩形DEFG的一边EF在BC上，其余两个顶点D，G分别在AB，AC上，则四边形DEFG的最大面积为（）

A、40 cm² B、20 cm² C、25 cm² D、10 cm²

查看试题解析
10. “幻方”最早记载于春秋时期的《大戴礼》中，现将1、2、3、4、5、7、8、9这8个数字填入如图1所示的“幻方”中，使得每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等．现有如图2所示的“幻方”，则（x-y）^m-n的值是（）

A、-27 B、-1 C、8 D、16

查看试题解析

二、填空题（每题2分，共16分）

11. 若m、n是方程x²－3x－1=0的解，则m²－4m－n的值是．

查看试题解析
12. 定义：关于x的方程 $a_{1} x^{2} + b_{1} x + c_{1} = 0$ （a₁≠0）与 $a_{2} x^{2} + b_{2} x + c_{2} = 0$ （a₂≠0），如果满足a₁+a₂＝0，b₁＝b₂ ， c₁+c₂＝0，则称这两个方程互为“对称方程”．若关于x的方程 $3 x^{2} + (m^{2} - 2 m + 3) x - 4 = 0$ 与 $- 3 x^{2} + 2 x + n = 0$ 互为“对称方程”，则 $(m - n)^{2}$ 的值为．

查看试题解析
13. 关于x的方程 $x^{2} - 2 x + m = p^{2}$ ，无论实数p取何值，该方程总有两个不相等的实数根，则实数m的取值范围为.

查看试题解析
14. 等腰三角形的三边的长是a 、b、4，其中a、b是方程x²-6x+c=0两个根，则此三角形的三边长是．

查看试题解析
15. 已知实数满足，则 $x^{2} + y^{2} + z^{2}$ 的值是.

查看试题解析
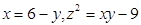16. 如果关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若（x﹣1）（mx﹣n）＝0是倍根方程，则 $\frac{2 n}{m}$ 的值为.

查看试题解析
17. 对于一个函数，当自变量x取n时，函数值y等于4－n，我们称n为这个函数的“二合点”，如果二次函数y＝mx²+x+1有两个相异的二合点x₁ ， x₂ ，且x₁＜x₂＜1，则m的取值范围是．

查看试题解析
18. 若a≠b，且 $a^{2} - 4 a + 1 = 0, b^{2} - 4 b + 1 = 0$ 则 $\frac{1}{1 + a^{2}} + \frac{1}{1 + b^{2}}$ 的值为

查看试题解析

三、解答题（共74分）

19. 已知实数a满足 $a^{2} + \frac{1}{a^{2}} - 2 a - \frac{2}{a} - 1 = 0$ ，求 $a + \frac{1}{a}$ 的值.

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} + c x + a = 0$ 的两个整数根恰好比方程 $x^{2} + a x + b = 0$ 的两个根都大1，求 $a + b + c$ 的值.

查看试题解析
21. 借鉴已有研究函数的经验，探索函数 $y = | x^{2} - 2 x - 3 | - 2$ 的图象与性质，研究过程如下，请补充完整.

(1)、自变量x的取值范围是全体实数，x与y的几组对应值列表如下：

其中： $m =$ ， $n =$ .

(2)、根据列表数据，在如图所示的平面直角坐标系中描点，并画出函数图象；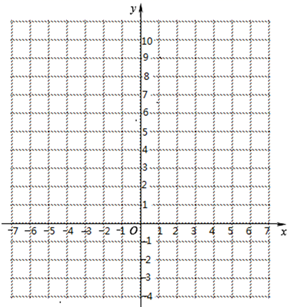

(3)、观察函数图象：
①写出函数的一条性质

②当方程 $| x^{2} - 2 x - 3 | = b + 2$ 有且仅有两个不相等的实数根，根据函数图象直接写出b的取值范围..

查看试题解析
22. 某连锁超市派遣调查小组在春节期间调查某种商品的销售情况，下面是调查后小张与其他两位成员交流的情况．
小张：“该商品的进价为24元/件．”

成员甲：“当定价为40元/件时，每天可售出480件．”

成员乙：“若单价每涨1元，则每天少售出20件；若单价每降1元，则每天多售出40件．”根据他们的对话，请你求出要使该商品每天获利7680元，应该怎样合理定价？

查看试题解析
23. 设a，b为实数，关于x的方程 $\frac{x}{x - 1} + \frac{x - 1}{x} = \frac{a + b x}{x^{2} - x}$ 无实数根，求代数式 $8 a + 4 b + | 8 a + 4 b - 5 |$ 的值.

查看试题解析
24. 如图，已知抛物线y=﹣x²﹣2x+m+1与x轴交于A（x₁ ， 0）、B（x₂ ， 0）两点，且x₁＜0，x₂＞0，与y轴交于点C，顶点为P．（提示：若x₁ ， x₂是一元二次方程ax²+bx+c=0（a≠0）的两个实根，则x₁+x₂=﹣ $\frac{b}{a}$ ，x₁•x₂= $\frac{c}{a}$ ）

(1)、求m的取值范围；

(2)、若OA=3OB，求抛物线的解析式；

(3)、在（2）中抛物线的对称轴PD上，存在点Q使得△BQC的周长最短，试求出点Q的坐标．

查看试题解析
25. 如图1，抛物线 $y ＝ x^{2} - (a + 1) x + a$ 与x轴交于A，B两点（点A位于点B的左侧），与y轴负半轴交于点C，若AB＝4.

(1)、求抛物线的解析式；

(2)、如图2，E是第三象限内抛物线上的动点，过点E作EF∥AC交抛物线于点F，过E作EG⊥x轴交AC于点M，过F作FH⊥x轴交AC于点N，当四边形EMNF的周长最大时，求点E的横坐标.

(3)、在x轴下方的抛物线上是否存在一点Q，使得以Q、C、B、O为顶点的四边形被对角线分成面积相等的两部分？如果存在，求点Q的坐标；如果不存在，请说明理由.

查看试题解析
26. 如图，在菱形ABCD中，m、n、t分别是菱形ABCD的两条对角线长和边长，这时我们把关于x的形如“mx²+2 $\sqrt{2}$ tx+n=0”的元二次方程称为“菱系一元二次方程”。请解决下列问题：

(1)、填空：
①当m=6，n=8时，t=

②用含m，n的代数式表示t²值，t²=

(2)、求证：关于x的“菱系一元二次方程” mx²+2 $\sqrt{2}$ tx+n=0必有实数根：

(3)、若x=-1是“菱系一元二次方程”mx²+2 $\sqrt{2}$ tx+n=0的一个根，且菱形的面积是25，BE是菱形ABCD的AD边上的高，求BE的值。

查看试题解析