2022年中考数学二轮专题复习-实数、整式及因式分解

试卷更新日期：2022-03-29 类型：二轮复习

进入出卷网下载

一、单选题

1. ${(a^{3})}^{2}$ 的值是（）

A、 $a^{6}$ B、 $a^{5}$ C、 $a^{9}$ D、 $- a^{6}$

查看试题解析
2. 互不重合的A，B，C三点在同一直线上，已知AC=2a+1，BC=a+4，AB=3a，这三点的位置关系是（）

A、点A在B，C两点之间 B、点B在A，C两点之间 C、点C在A，B两点之间 D、无法确定

查看试题解析
3. 下列因式分解正确的是（）

A、x²＋9＝(x＋3)(x﹣3) B、x²＋x﹣6＝（x﹣2）（x＋3） C、3x﹣6y＋3＝3（x﹣2y） D、x²＋2x﹣1＝(x﹣1)²

查看试题解析
4. 已知 $(- x) (2 x^{2} - a x - 1) - 2 x^{3} + 3 x^{2}$ 中不含 $x$ 的二次项，则 $a$ 的值是（）

A、3 B、2 C、-3 D、-2

查看试题解析
5. 如果单项式 $3 x y^{n}$ 和 $- 4 x^{m} y^{2}$ 是同类项，则m和n的值是（）

A、2，1 B、-2，1 C、-1，2 D、 $1$ ， $2$

查看试题解析
6. 设 $(x^{m - 1} y^{n + 2}) (x^{5 m} y^{2}) = x^{5} y^{7}$ ，则 ${(- \frac{1}{2} m)}^{n}$ 的值为（　　）

A、 $- \frac{1}{8}$ B、 $- \frac{1}{2}$ C、1 D、 $\frac{1}{2}$

查看试题解析
7. 下列计算中错误的是（　　）

A、4a⁵b³c²÷（﹣2a²bc）²＝ab B、（a+1）（a﹣1）（a²+1）＝a⁴﹣1 C、4x²y•（﹣ $\frac{1}{2}$ y）÷4x²y²＝﹣ $\frac{1}{2}$ D、25×（ $\frac{1}{25}$ x²﹣ $\frac{1}{10}$ x+1）＝x²﹣ $\frac{5}{2}$ x+1

查看试题解析
8. 若代数式 $a x^{2} + 4 x - y + 3 - (2 x^{2} - b x + 5 y - 1)$ 的值与x的取值无关，则 $a + b$ 的值为（）

A、6 B、－6 C、2 D、－2

查看试题解析
9. 若 $A$ 与 $- \frac{1}{2} a b$ 的积为 $- 4 a^{3} b^{3} + 3 a^{2} b^{2} - \frac{1}{2} a b$ ，则 $A$ 为（）

A、 $- 8 a^{2} b^{2} + 6 a b - 1$ B、 $- 2 a^{2} b^{2} + \frac{3}{2} a b + \frac{1}{4}$ C、 $8 a^{2} b^{2} - 6 a b + 1$ D、 $2 a^{2} b^{2} - \frac{3}{2} a b + 1$

查看试题解析
10. 已知 $(x - 5) (x + ☆) = x^{2} - 2 x - 15$ ，其中☆代表一个常数，则☆的值为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 把五张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个大长方形(长为m，宽为n内(如图②)，大长方形未被卡片覆盖的部分用阴影表示.当m不变，n变长时，阴影部分的面积差总保持不变，则a，b应满足的关系为（ )

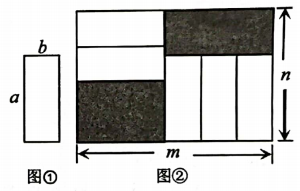A、a=5b B、a=3b C、a=2b D、 $a = \frac{3}{2} b$

查看试题解析
12. 如图，点A、B、C在数轴上表示的数分别为a、b、c，且OA+OB=OC，则下列结论中：
①abc＜0；②a（b+c）＞0；③a﹣c=b；④ $\frac{| a |}{a} + \frac{b}{| b |} + \frac{| c |}{c} = 1$ ．

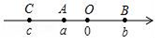
其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
13. 有两个正方形A，B.现将B放在A的内部得图甲，将A，B构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12，若三个正方形A和两个正方形B得图丙，则阴影部分的面积为（　　）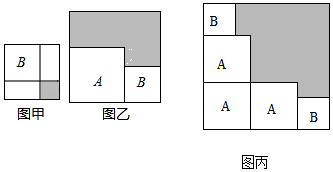

A、28 B、29 C、30 D、31

查看试题解析
14. $2 \times (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1)$ 的计算结果的个位数字是（）

A、8 B、6 C、2 D、0

查看试题解析
15. 已知 $a^{2} + \frac{1}{4} b^{2} = 2 a - b - 2$ ，则 $3 a - \frac{1}{2} b$ 的值为（）

A、4 B、2 C、-2 D、-4

查看试题解析

二、填空题

16. $2 a^{n}$ 与 $- a^{2}$ 是同类项.则常数n的值为.

查看试题解析
17. 化简：（8x³y³﹣4x²y²）÷2xy²＝.

查看试题解析
18. 有理数 $a$ ， $b$ ， $c$ 在数轴上表示的点如图所示，化简 $| a + b | - | a - c | - 2 | b + c | =$ .

查看试题解析
19. 已知： $x + \frac{1}{x} = 3$ ，则 $x^{2} + \frac{1}{x^{2}} =$ .

查看试题解析
20. 当a＝时，多项式x²﹣2（a﹣1）x+25是一个完全平方式．

查看试题解析
21. 如图，面积为3的正方形ABCD的顶点A在数轴上，且表示的数为-2，若AB=AE，则数轴上点E所表示的数为．

查看试题解析
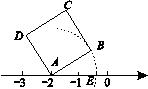22. 已知某三角形第一条边长为 $（ 3 a - 2 b ）$ cm，第二条边比第一条边长 $（ a + 2 b ）$ cm，第三条边比第一条边的2倍少bcm，则这个三角形的周长为cm．

查看试题解析
23. 阅读理解：如果一个数的平方等于﹣1，记为i²＝﹣1，i叫做虚数单位，我们把形如a+bi（a、b为实数，且b≠0）的数叫做复数，其中a叫这个复数的实部，b叫这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.
如：（4+i）+（6﹣2i）＝（4+6）+（1﹣2）i＝10﹣i；

（2﹣i）（3+i）＝2×3+2i﹣3i﹣i²＝6﹣i﹣（﹣1）＝7﹣i.

根据以上信息，计算（3+i）（1﹣3i）＝.

查看试题解析
24. 设M＝x+y，N＝x﹣y，P＝xy．若M＝1，N＝2，则P＝．

查看试题解析
25. 若2^a=3.2^b=5，2^c= $\frac{15}{4}$ ，则用含a，b的代数式表示c为.

查看试题解析
26. 若 $x + y + z = 0$ ，且x，y，z均不为零，则 $\frac{x}{| x |} + \frac{| y |}{y} + \frac{z}{| z |}$ 的值为．

查看试题解析
27. 已知正实数x，y，z满足：xy+yz+zx≠1，且 $\frac{(x^{2} - 1) (y^{2} - 1)}{x y} + \frac{(y^{2} - 1) (z^{2} - 1)}{y z} + \frac{(z^{2} - 1) (x^{2} - 1)}{z x}$ =4.求 $\frac{1}{x y} + \frac{1}{y z} + \frac{1}{z x}$ 的值为.

查看试题解析
28. 两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为S₁；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S₂ ．若a+b＝8，ab＝10，则S₁+S₂=；当S₁+S₂＝40时，则图3中阴影部分的面积S₃=.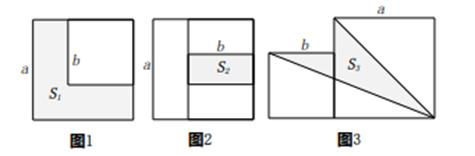

查看试题解析
29. 如图，在长方形ABCD中，AB<BC，点P为长方形内部一点，过点P分别作PE⊥BC于点E、PF⊥CD于点F，分别以PF、CF为边作正方形PMNF，正方形GHCF，若两个正方形的面积之和为42，长方形PECF的面积为11，BE=DF=2，则长方形ABCD的面积为.

查看试题解析
30. 我国宋朝数学家杨辉在他的著作 $《$ 解：九章算法 $》$ 中提出“杨辉三角” $($ 如图 $)$ ，此图揭示了 ${(a + b)}^{n} (n$ 为非负整数 $)$ 展开式的项数及各项系数的有关规律.
例如： ${(a + b)}^{0} = 1$ ，它只有一项，系数为1；系数和为1；

${(a + b)}^{1} = a + b$ ，它有两项，系数分别为1，1，系数和为2；

${(a + b)}^{2} = a^{2} + 2 ab + b^{2}$ ，它有三项，系数分别为1，2，1，系数和为4；

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 {ab}^{2} + b^{3}$ ，它有四项，系数分别为1，3，3，1，系数和为8； $\dots$ ，

则 ${(a + b)}^{n}$ 的展开式共有项，系数和为.

查看试题解析

三、计算题

31. 计算.

(1)、10²×10⁵

(2)、x·x⁵ $\cdot$ x⁷

(3)、a²·（-a）⁴

(4)、x^2m+1·x^m

查看试题解析
32. 先化简，再求值： $(a^{2} - a b - 7) - (- 4 a^{2} + 2 a b + 7)$ ，其中 $a = 2 ， b = \frac{3}{2}$ ．

查看试题解析
33. 分解因式.

(1)、 $x^{3} - x$ ；

(2)、 $2 a^{2} - 4 a + 2$ ；

(3)、 $5 x^{3} - 10 x^{2} + 5 x$ ；

(4)、 $x^{2} (x - 2) - 16 (x - 2)$ .

查看试题解析

四、解答题

34. 先化简，再求值： $2 m^{2} - [4 (\frac{1}{2} m^{2} + n^{2} - 2 m n) - 2 (\frac{3}{2} n^{2} - 5 m n)] - \frac{1}{3} n^{2}$ ，其中 $| m + 4 | + \sqrt{n + 3} = 0$ .

查看试题解析
35. 小明在进行两个多项式的乘法运算时，不小心把乘 $(x - 2 y)$ 错抄成除以 $(x - 2 y)$ ，结果得到 $3 x$ ，如果小明没有错抄题目，并且计算依然符合题意，那么得到的结果应该是什么？

查看试题解析
36. 在一个边长为（ $\sqrt{3} + \sqrt{5}$ ）cm的正方形内部挖去一个边长为（ $\sqrt{5} - \sqrt{3}$ ）cm的正方形（如图所示），求剩余阴影部分图形的面积．

查看试题解析
37. 某种产品的原料提价，因而厂家决定对产品进行提价，现有三种方案：
①第一次提价p%，第二次提价q%；

②第一次提价q%，第二次提价p%；

③第一、二次提价均为 $\frac{p + q}{2} %$ .

其中p，q是不相等的正数，三种方案哪种提价最多？

查看试题解析
38. 一次函数 $y = a x + b (b \neq 0)$ 与一次函数 $y = 2 - c x$ 的图象的交点的纵坐标为 $a + b$ ， $\frac{{(1 - a)}^{2}}{b c} + \frac{{(1 - b)}^{2}}{a c} + \frac{{(1 - c)}^{2}}{a b} = 3$ ．

(1)、求ab+bc+ca的值；

(2)、当 $a \neq 1, b \neq 1$ 时，求证： $\frac{b}{{(1 - a)}^{2}} = \frac{a}{{(1 - b)}^{2}}$ .

查看试题解析
39. 阅读下面的文字，解答问题：大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $\sqrt{2}$ -1来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法是有道理，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分。

又例如：

∵ $\sqrt{4}$ < $\sqrt{7}$ < $\sqrt{9}$ ，即2< $\sqrt{7}$ <3，

∴ $\sqrt{7}$ 的整数部分为2，小数部分为( $\sqrt{7}$ -2)．

请解答：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是。

(2)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，求a+b- $\sqrt{5}$ 的值；

(3)、已知：10+ $\sqrt{3}$ =x+y，其中x是整数，且0<y<1，求x-y的相反数。

查看试题解析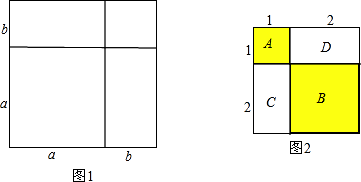
40. 问题再现：
数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．
例如：利用图形的几何意义证明完全平方公式．
证明：将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1：
这个图形的面积可以表示成：
（a+b）²或 a²+2ab+b²
∴（a+b）²=a²+2ab+b²
这就验证了两数和的完全平方公式．
类比解决：
①请你类比上述方法，利用图形的几何意义证明平方差公式．（要求画出图形并写出推理过程）
问题提出：如何利用图形几何意义的方法证明：1³+2³=3²？
如图2，A表示1个1×1的正方形，即：1×1×1=1³
B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=2³
而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．
由此可得：1³+2³=（1+2）²=3²
尝试解决：
②请你类比上述推导过程，利用图形的几何意义确定：1³+2³+3³= ▲ ．（要求写出结论并构造图形写出推证过程）．
问题拓广：
③请用上面的表示几何图形面积的方法探究：1³+2³+3³+…+n³= ▲ ．（直接写出结论即可，不必写出解题过程）

查看试题解析

五、综合题

41. 阅读理解.“若 $x$ 满足 $(70 - x) (x - 20) = 30$ ，求 ${(70 - x)}^{2} + {(x - 20)}^{2}$ 的值”.
解：设 $(70 - x) = a ， (x - 20) = b$ ，

则 $(70 - x) (x - 20) = a b = 30 ， a + b = (70 - x) + (x - 20) = 50$ ，

那么 ${(70 - x)}^{2} + {(x - 20)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 50^{2} - 2 \times 30 = 2440$ .

解决问题.

(1)、若 $x$ 满足 $(40 - x) (x - 10) = - 10$ ，求 ${(40 - x)}^{2} + {(x - 10)}^{2}$ 的值；

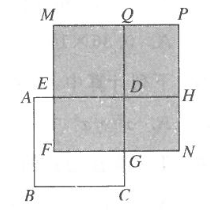(2)、若 $x$ 满足 ${(2021 - x)}^{2} + {(2020 - x)}^{2} = 4321$ ，求 $(2021 - x) (2020 - x)$ 的值；

(3)、如图，正方形ABCD的边长为 $x ， A E = 14 ， C G = 30$ ，长方形EFGD的面积是500，四边形NGDH和MEDQ都是正方形，四边形PQDH是长方形，求图中阴影部分的面积.(结果必须是一个具体的数值).

查看试题解析