福建省名校联盟全国优质校2022届高三数学大联考试卷

试卷更新日期：2022-03-28 类型：高考模拟

进入出卷网下载

一、单选题

1. 若集合 $A = {y | y = 2^{x} ， x \geq 0}$ ， $B = {x | y = l o g_{2} (2 - x)}$ ，则 $A ∩ B =$ （）

A、 ${x | 1 < x < 2}$ B、 ${x | x \geq 1}$ C、 ${x | 1 \leq x < 2}$ D、 ${x | x < 2}$

查看试题解析
2. 若复数 $z$ 满足 $z = \frac{3 - 2 i}{1 + i}$ ，则 $z$ 在复平面内对应的点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知数列 ${a_{n}}$ 为等比数列，则“ $a_{5}$ ， $a_{7}$ 是方程 $x^{2} + 2022 x + 1 = 0$ 的两实根”是” $a_{6} = 1$ ，或 $a_{6} = - 1$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 函数 $f (x) = (3 x - x^{3}) \sin x$ 的部分图象大致为（）

A、 B、 C、 D、

查看试题解析
5. 从4名男同学和3名女同学中任选2名同学，在选到的都是同性别同学的条件下，都是男同学的概率是（）

A、 $\frac{3}{5}$ B、 $\frac{4}{7}$ C、 $\frac{3}{4}$ D、 $\frac{2}{3}$

查看试题解析
6. 已知 $a = 2^{0.5} ， b = l o g_{3} 6 ， c = l o g_{4} 8$ ，则 $a$ ， $b$ ， $c$ 的大小关系是（）

A、 $a > b > c$ B、 $b > c > a$ C、 $b > a > c$ D、 $c > a > b$

查看试题解析
7. 若 $c o s 2 α = 1 + 2 c o s α$ ，则 $s i n^{2} α + s i n^{4} α$ 的值为（）

A、 $\sqrt{5} - 1$ B、 $\frac{\sqrt{5} - 1}{2}$ C、1 D、 $\sqrt{2}$

查看试题解析
8. 传说，意大利的西西里岛有个山洞是用来关押罪犯的，罪犯们曾多次密谋商议逃跑，但不管多完美的计划都会被狱卒发现，原来山洞内的空间是一个椭球体，最大截面部分是一个椭圆面，罪犯和狱卒所待的地方正好是椭圆的两个焦点，罪犯们说的话经过洞壁的反射，最终都传向了狱警所在的地方，即椭圆的另一个焦点，这里面含着椭圆的光学性质.请利用椭圆的该性质解决下列问题：已知 $P$ 是椭圆 $C$ ： $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 上的点. $F_{1}$ 、 $F_{2}$ 是椭圆 $C$ 的左右焦点， $c o s ∠ F_{1} P F_{2} = \frac{3}{4}$ ， $O$ 为坐标原点， $O$ 到椭圆 $C$ 在 $P$ 处的切线的距离为（）

A、 $\frac{3}{2}$ B、 $\frac{\sqrt{14}}{2}$ C、 $\frac{\sqrt{14}}{3}$ D、 $\frac{5}{3}$

查看试题解析

二、多选题

9. 在研究某种产品的零售价 $x$ （单位：元）与销售量 $y$ （单位：万件）之间的关系时，根据所得数据得到如下所示的对应表：
$x$
12
14
16
18
20
$y$
17
16
14
13
11
利用最小二乘法计算数据，得到的回归直线方程为： $\hat{y} = \hat{b} x + 26.2$ ，则下列说法中正确的是（）

A、 $\hat{b} > 0$ B、 $\hat{b} < 0$ C、回归直线必过点(16，14.2) D、若该产品的零售价定为22元，则销售一定是9.7万件

查看试题解析
10. 已知向量 $\vec{a} = (- 1 ， 2)$ ， $\vec{b} = (1 ， m)$ ，则（）

A、若 $\vec{a}$ 与 $\vec{b}$ 垂直，则 $m = \frac{1}{2}$ B、若 $\vec{a} / / \vec{b}$ ，则 $m$ 的值为-2 C、若 $| \vec{a} | = | \vec{b} |$ ，则 $m = 2$ D、若 $m = 3$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为45°

查看试题解析
11. 已知 ${a_{n}}$ 是正项等差数列，其公差为 $d$ ，若存在常数 $c$ ，使得对任意正整数 $n$ 均有 $\frac{2}{a_{n + 1}} = \frac{c}{a_{n}} + \frac{a_{n}}{c}$ ，则以下判断不正确的是（）

A、 $d > 0$ B、d=0 C、 $c > 1$ D、 $0 < c < 1$

查看试题解析
12. 已知A，B，C，D是表面积为20π的球体表面上四点，且 $A B = 2$ ， $C D = 4$ ，则（）

A、若 $A B / / C D$ ，则平行直线AB与CD间距离的最大值为3 B、若 $A B / / C D$ ，则平行直线AB与CD间距离的最小值为 $\sqrt{3}$ C、若A，B，C，D四点能构成三棱锥，则该三棱锥体积的最大值为4 D、若 $A C = 2 \sqrt{5}$ ，则 $A C ⊥ A D$

查看试题解析

三、填空题

13. 现有一个橡皮泥制作的实心圆柱，其底面半径、高均为1，将它重新制作成一个体积与高不变的圆锥，则该圆锥的底面积为.

查看试题解析
14. 二项式 $(\sqrt{x} - \sqrt[3]{x})^{5}$ 的展开式中含 $x^{2}$ 的项的系数是.（用数字作答）

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} x + 1 ， x \leq 0 \\ l n x ， x ＞ 0 \end{array}$ ，若 $f (x_{1}) = f (x_{2})$ 且 $x_{1} ＜ x_{2}$ ，则 $x_{2} - 2 x_{1}$ 的最小值为.

查看试题解析
16. 已知函数 $f (x) = 2 s i n (ω x - \frac{π}{6}) - 1$ ，其中 $ω > 0$ ，若 $f (x)$ 在区间( $\frac{π}{4}$ ， $\frac{2 π}{3}$ )上恰有2个零点，则 $ω$ 的取值范围是.

查看试题解析

四、解答题

17. 已知 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为a， $b$ ， c， $2 c - b = 2 a c o s B$ .

(1)、求角A；

(2)、若 $\frac{\sqrt{3} b}{2} s i n B + (c - \frac{b}{2}) c o s B = \sqrt{7}$ ， $b - c = 2$ ，求 $B C$ 边上的高.

查看试题解析
18. $S_{n}$ 为数列 ${a_{n}}$ 的前 $n$ 项和，已知 $4 S_{n} = a_{n}^{2} + 2 a_{n} - 3$ ，且 $a_{n} > 0$ .

(1)、求数列 ${a_{n}}$ 的通项公式 $a_{n}$ ；

(2)、数列 $b_{n}$ 依次为： $a_{1}$ ， 2、 $a_{2}$ ， $2^{2}$ ， $2^{3}$ ， $a_{3}$ ， $2^{4}$ ， $2^{5}$ ， $2^{6}$ ， $a_{4}$ ， $2^{7}$ ， $2^{8}$ ， $2^{9}$ ， $2^{10} ⋯$ ，规律是在 $a_{k}$ 和 $a_{k + 1}$ 中间插入 $k$ 项，所有插入的项构成以2为首项，2为公比的等比数列，求数列 ${b_{n}}$ 的前50项的和.

查看试题解析
19. 为了买到包括星黛露毛线玩具，达菲雪莉玫和星黛露毛绒玩具钥匙圈等商品，12月29日凌晨，约5000名游客在上海迪士尼外夜排长龙，此现象在网络上引发了广泛讨论.为了解广大民对下通玩偶的喜爱程度，某市一玩具商城随机抽取了100名市民，以分数表示对卡通玩偶的喜爱程度（喜爱程度越高，分数越高，满分为100分）到如下频率分布直方图.

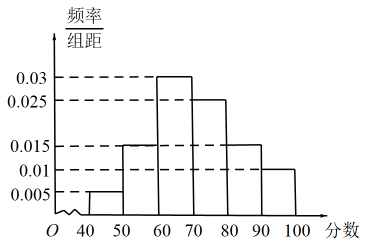(1)、试估计该市市民对卡通玩偶平均喜爱程度的分数值；

(2)、用上述100名市民对玩偶喜爱程度分数值的频率分布估算所有排队游客分数值的概率分布，在所有游客中随机抽取2人，对分数值在区间 $[70 ， 80)$ 内的游客送一个玩偶，分数值在区间 $[80 ， 100]$ 内的游客赠送两个玩偶，分数值低于70分的游客不送玩偶，记总共送出的玩偶个数为 $X$ ，求 $E (X)$ .

查看试题解析
20. 如图，四棱锥 $P - A B C D$ 中， $A D = A B = \sqrt{2}$ ， $C D = C B = \sqrt{5}$ ， $B D = 2$ ， $P B = P D$ ， $E$ 为线段 $P C$ 上一点， $P A / /$ 平面 $B D E$ ，平面 $P D B ⊥$ 平面 $A B C D$ .

(1)、求 $\frac{P E}{P C}$ ；

(2)、若三棱锥 $P - B D E$ 体积为 $\frac{2}{3}$ ，求二面角 $E - B C - D$ 的余弦值.

查看试题解析
21. 设抛物线E： $y^{2} = 2 p x (p > 0)$ 的焦点为F，抛物线上一点 $P (x_{0} ， 2)$ 满足 $| P F | = 2$ .

(1)、求抛物线E的方程；

(2)、两不同直线 $l_{1}$ ， $l_{2}$ 均过点F，且 $l_{1}$ 交抛物线E于 $A$ ， $C$ 两点， $l_{2}$ 交抛物线 $E$ 于B，D两点.设直线AB和CD分别与 $x$ 轴交于点 $M (x_{1} ， 0)$ 和点 $N (x_{2} ， 0)$ ，求 $x_{1} x_{2}$ 的值.

查看试题解析
22. 已知函数 $f (x) = (x - k) (l n x - k)$ ，其中 $k \geq 0$ .

(1)、若定义在 $(0 ， + ∞)$ 上的函数 $g (x)$ 满足 $g^{'} (x) = f (x)$ ，求 $g (x)$ 的单调区间；

(2)、证明： $f (x)$ 有唯一极值点 $x_{0}$ ，且 $f (x_{0}) \leq - \frac{1}{4}$ .

查看试题解析

$x$	12	14	16	18	20
$y$	17	16	14	13	11