2022年初中数学浙教版九年级下册第三章三视图与表面展开图 能力阶梯训练——普通版
试卷更新日期:2022-03-27 类型:单元试卷
一、单选题
-
1. 如图是由6个相同的小立方体堆成的几何体的俯视图,小正方形中的数字表示该位置小立方体的个数,则这个几何体的主视图是( )
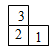 A、
A、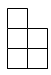 B、
B、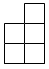 C、
C、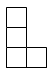 D、
D、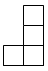 2. 下图是一个正方体盒子的展开图,把展开图折叠成小正方体后,“御”字所在面的相对面上的字是( )
2. 下图是一个正方体盒子的展开图,把展开图折叠成小正方体后,“御”字所在面的相对面上的字是( ) A、射 B、乐 C、数 D、礼3. 如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( )
A、射 B、乐 C、数 D、礼3. 如图,在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为5米,则这棵树的高度为( ) A、7.8米 B、3.2米 C、2.30米 D、1.5米4. 如图,王华晚上由路灯A下的B处走到C处时,测得影子 的长为1m,继续往前走3m到达E处时,测得影子 的长为2m,已知王华的身高是1.5m,那么路灯A的高度 等于( )
A、7.8米 B、3.2米 C、2.30米 D、1.5米4. 如图,王华晚上由路灯A下的B处走到C处时,测得影子 的长为1m,继续往前走3m到达E处时,测得影子 的长为2m,已知王华的身高是1.5m,那么路灯A的高度 等于( )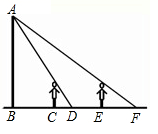 A、4.5m B、6m C、7.5m D、8m5. 几何体的三视图如图所示,这个几何体是( )
A、4.5m B、6m C、7.5m D、8m5. 几何体的三视图如图所示,这个几何体是( )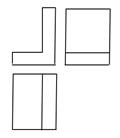 A、
A、 B、
B、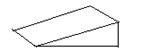 C、
C、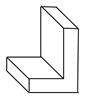 D、
D、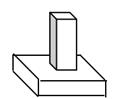 6. 如图,已知圆锥侧面展开图的扇形面积为65 cm2,扇形的弧长为10 cm,则圆锥母线长是( )
6. 如图,已知圆锥侧面展开图的扇形面积为65 cm2,扇形的弧长为10 cm,则圆锥母线长是( )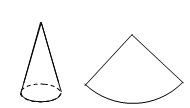 A、5cm B、10cm C、12cm D、13cm7. 如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A、5cm B、10cm C、12cm D、13cm7. 如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )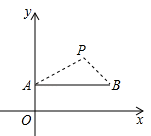 A、3 B、4 C、5 D、68. 如图所示,矩形纸片ABCD中,AB=4cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AD的长为( )
A、3 B、4 C、5 D、68. 如图所示,矩形纸片ABCD中,AB=4cm,把它分割成正方形纸片ABFE和矩形纸片EFCD后,分别裁出扇形ABF和半径最大的圆,恰好能作为一个圆锥的侧面和底面,则AD的长为( ) A、8cm B、7cm C、6cm D、5cm9. 某校积极开展综合实践活动,一次九年级数学小组发现校园里有一棵被强台风摧折的大树,其残留的树桩DC的影子的一端E刚好与倒地的树梢重合,于是他们马上利用其测量旁边钟楼AB的高度.如图是根据测量活动场景抽象出的平面图形.活动中测得的数据如下:
A、8cm B、7cm C、6cm D、5cm9. 某校积极开展综合实践活动,一次九年级数学小组发现校园里有一棵被强台风摧折的大树,其残留的树桩DC的影子的一端E刚好与倒地的树梢重合,于是他们马上利用其测量旁边钟楼AB的高度.如图是根据测量活动场景抽象出的平面图形.活动中测得的数据如下:
①大树被摧折倒下的部分DE=10m;
②tan∠CDE= ;
③点E到钟楼底部的距离EB=7m;
④钟楼AB的影长BF=(20 +8)m;
⑤从D点看钟楼顶端A点的仰角为60°.
(点C , E , B , F在一条直线上).
请你选择几个需要的数据,用你喜欢的方法求钟楼AB的高度,则AB=( )
A、15 m B、(15 +6)m C、(12 +6)m D、15m10. 如图,线段 ,点 、 在 上, .已知点 从点 出发,以每秒1个单位长度的速度沿着 向点 移动,到达点 后停止移动,在点 移动过程中作如下操作:先以点 为圆心, 、 的长为半径分别作两个圆心角均为60°的扇形,再将两个扇形分别围成两个圆锥的侧面.设点 的移动时间为(秒).两个圆锥的底面面积之和为 .则 关于 的函数图象大致是( )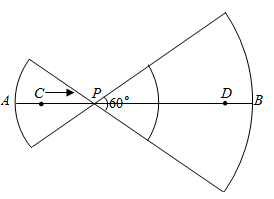 A、
A、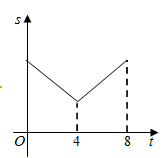 B、
B、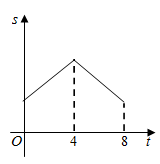 C、
C、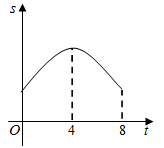 D、
D、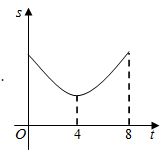
二、填空题
-
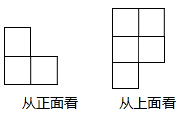
11. 若一个圆锥的母线长为4,底面半径是1,则它的侧面展开图的面积是 .12. 一个几何体由若干大小相同的小立方块搭成,如图分别是从它的正面、上面看到的形状图,则该几何体至少是用 个小立方块搭成的.
 13. 如图,圆锥的底面半径 为 ,高 为 ,则圆锥的侧面积为 .
13. 如图,圆锥的底面半径 为 ,高 为 ,则圆锥的侧面积为 .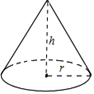 14. 在如图所示的网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,点都是格点,若图中扇形是一个圆锥的侧面展开图,则该圆锥底面圆的半径为.
14. 在如图所示的网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,点都是格点,若图中扇形是一个圆锥的侧面展开图,则该圆锥底面圆的半径为. 15. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长 为 ,扇形的圆心角 ,则圆锥的底面圆半径 为 .
15. 如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长 为 ,扇形的圆心角 ,则圆锥的底面圆半径 为 . 16. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.
16. 一张长50cm,宽40cm的长方形纸板,在其四个角上分别剪去一个小正方形(边长相等且为整厘米数)后,折成一个无盖的长方体形盒子,这个长方体形盒子的容积最大为cm3.三、综合题
-
17. 用若干个大小相同的小立方块搭建一个几何体,从正面和上面观察这个几何体得到下面两幅形状图.


(从正面看) (从上面看)
(1)、请画出一种从左面看这个几何体得到的形状图;(2)、搭建这个几何体最少要用a=个小立方块,最多用b=个小立方块;(3)、在(2)的条件下,若有理数x,y满足 , ,且 ,求 的值.18. 如图,A、B、C分别表示甲、乙、丙三个物体的顶端,甲物体高3米,影长2米,乙物体高2米,影长3米,甲乙两物体相距4米. (1)、请在图中画出光源灯的位置及灯杆,并画出物体丙的影子.(2)、若甲、乙、丙及灯杆都与地面垂直,且在同一直线上,求灯杆的高度.19. 如图所示的是一个正方体的展开图,折成正方体后,x,y与其相对面上的数字相等,求xy的值.
(1)、请在图中画出光源灯的位置及灯杆,并画出物体丙的影子.(2)、若甲、乙、丙及灯杆都与地面垂直,且在同一直线上,求灯杆的高度.19. 如图所示的是一个正方体的展开图,折成正方体后,x,y与其相对面上的数字相等,求xy的值.
 20. 如图,公路旁有两个高度相等的路灯AB、CD,小明上午上学时发现路灯AB在太阳光下的影子恰好落在路牌底部E处,他自己的影子恰好落在路灯CD的底部C处;晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在E处.
20. 如图,公路旁有两个高度相等的路灯AB、CD,小明上午上学时发现路灯AB在太阳光下的影子恰好落在路牌底部E处,他自己的影子恰好落在路灯CD的底部C处;晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在E处. (1)、在图中画出小明的位置(用线段FG表示).(2)、若上午上学时,高1米的木棒的影子为2米,小明身高为1.5米,他距离路牌底部E恰好2米,求路灯高.21. 小明同学要测量学校旗杆AB的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为0.8米,同时测量旗杆AB的影长时,由于影子不全落在地面上,他测得地面上的影长BC为6米,留在墙上的影高CD为3米,请利用以上信息,求旗杆AB的高度.
(1)、在图中画出小明的位置(用线段FG表示).(2)、若上午上学时,高1米的木棒的影子为2米,小明身高为1.5米,他距离路牌底部E恰好2米,求路灯高.21. 小明同学要测量学校旗杆AB的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为0.8米,同时测量旗杆AB的影长时,由于影子不全落在地面上,他测得地面上的影长BC为6米,留在墙上的影高CD为3米,请利用以上信息,求旗杆AB的高度.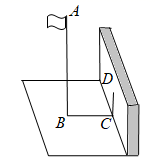 22. 【综合与实践】现实生活中,人们可以借助光源来测量物体的高度.已知榕树CD,FG和灯柱AB如图①所示,在灯柱AB上有一盏路灯P,榕树和灯柱的底端在同一水平线上,两棵榕树在路灯下都有影子,只要测量出其中一些数据,则可求出所需要的数据,具体操作步骤如下:
22. 【综合与实践】现实生活中,人们可以借助光源来测量物体的高度.已知榕树CD,FG和灯柱AB如图①所示,在灯柱AB上有一盏路灯P,榕树和灯柱的底端在同一水平线上,两棵榕树在路灯下都有影子,只要测量出其中一些数据,则可求出所需要的数据,具体操作步骤如下: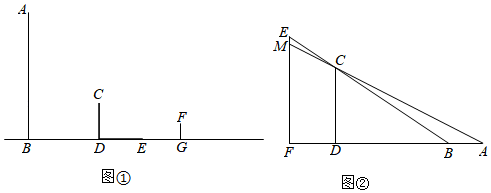
①根据光源确定榕树在地面上的影子;
②测量出相关数据,如高度,影长等;
③利用相似三角形的相关知识,可求出所需要的数据.
根据上述内容,解答下列问题:
(1)、已知榕树CD在路灯下的影子为DE,请画出榕树FG在路灯下的影子GH;(2)、如图①,若榕树CD的高度为3.6米,其离路灯的距离BD为6米,两棵榕树的影长DE,GH均为4米,两棵树之间的距离DG为6米,求榕树FG的高度;(3)、无论太阳光还是点光源,其本质与视线问题相同.日常生活中我们也可以直接利用视线解决问题.如图②,建筑物CD高为50米,建筑物MF上有一个广告牌EM,合计总高度EF为70米,两座建筑物之间的直线距离FD为30米.一个观测者(身高不计)先站在A处观测,发现能看见广告牌EM的底端M处,观测者沿着直线AF向前走了5米到B处观测,发现刚好看到广告牌EM的顶端E处.则广告牌EM的高度为 米.23. 长方体的长为20cm,宽为10cm,高为15cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖,需要爬行的最短距离是多少? 24. 测量金字塔高度:如图1,金字塔是正四棱锥 ,点O是正方形 的中心 垂直于地面,是正四棱锥 的高,泰勒斯借助太阳光.测量金字塔影子 的相关数据,利用平行投影测算出了金字塔的高度,受此启发,人们对甲、乙、丙三个金字塔高度也进行了测量.甲、乙、丙三个金字塔都用图1的正四棱锥 表示.
24. 测量金字塔高度:如图1,金字塔是正四棱锥 ,点O是正方形 的中心 垂直于地面,是正四棱锥 的高,泰勒斯借助太阳光.测量金字塔影子 的相关数据,利用平行投影测算出了金字塔的高度,受此启发,人们对甲、乙、丙三个金字塔高度也进行了测量.甲、乙、丙三个金字塔都用图1的正四棱锥 表示. (1)、测量甲金字塔高度:如图2,是甲金字塔的俯视图,测得底座正方形 的边长为 ,金字塔甲的影子是 ,此刻,1米的标杆影长为0.7米,则甲金字塔的高度为m.(2)、测量乙金字塔高度:如图1,乙金字塔底座正方形 边长为 ,金字塔乙的影子是 , ,此刻1米的标杆影长为0.8米,请利用已测出的数据,计算乙金字塔的高度.
(1)、测量甲金字塔高度:如图2,是甲金字塔的俯视图,测得底座正方形 的边长为 ,金字塔甲的影子是 ,此刻,1米的标杆影长为0.7米,则甲金字塔的高度为m.(2)、测量乙金字塔高度:如图1,乙金字塔底座正方形 边长为 ,金字塔乙的影子是 , ,此刻1米的标杆影长为0.8米,请利用已测出的数据,计算乙金字塔的高度.