2022年初中数学浙教版九年级下册第三章三视图与表面展开图 能力阶梯训练——容易版
试卷更新日期:2022-03-27 类型:单元试卷
一、单选题
-
1. 下面几何体中,从正面看到的平面图形为三角形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下图所示的几何体是由五个相同的小正方体搭建而成,则其左视图为( )
2. 下图所示的几何体是由五个相同的小正方体搭建而成,则其左视图为( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是( )A、
3. 分别观察下列几何体,其中主视图、左视图和俯视图完全相同的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列4个平面图形中,能够围成圆柱侧面的是( )A、
4. 下列4个平面图形中,能够围成圆柱侧面的是( )A、 B、
B、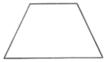 C、
C、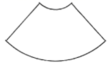 D、
D、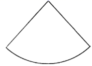 5. 如图,三视图正确的是( )
5. 如图,三视图正确的是( ) A、
A、 主视图
B、
主视图
B、 左视图
C、
左视图
C、 左视图
D、
左视图
D、 俯视图
6. 如图是一个几何体的表面展开图,这个几何体是( )
俯视图
6. 如图是一个几何体的表面展开图,这个几何体是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 以下哪个图形经过折叠可以得到正方体( )A、
7. 以下哪个图形经过折叠可以得到正方体( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为 , 扇形的圆心角等于120°,则围成的圆锥模型的高为( ).
8. 如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为 , 扇形的圆心角等于120°,则围成的圆锥模型的高为( ). A、 B、 C、 D、9. 如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面距离BC=1米,已知某一时刻BC在地面的影长CN=1.5米,AC在地面的影长CM=4.5米,则AB高为( )
A、 B、 C、 D、9. 如图,AB表示一个窗户的高,AM和BN表示射入室内的光线,窗户的下端到地面距离BC=1米,已知某一时刻BC在地面的影长CN=1.5米,AC在地面的影长CM=4.5米,则AB高为( )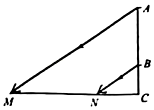 A、3.5 B、2 C、1.5 D、2.510. 如图,王华晚上由路灯A下的B处走到C处时,测得影子 的长为1m,继续往前走3m到达E处时,测得影子 的长为2m,已知王华的身高是1.5m,那么路灯A的高度 等于( )
A、3.5 B、2 C、1.5 D、2.510. 如图,王华晚上由路灯A下的B处走到C处时,测得影子 的长为1m,继续往前走3m到达E处时,测得影子 的长为2m,已知王华的身高是1.5m,那么路灯A的高度 等于( )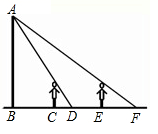 A、4.5m B、6m C、7.5m D、8m
A、4.5m B、6m C、7.5m D、8m二、填空题
-
11. 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图是正方体的平面展开图,若图中的“锦”表示正方体的右面,则“”表示正方体的左面
 12. 下列是由4个大小相同的小立方块搭成的几何体,从正面和从左面看得到的形状图相同的是( )A、
12. 下列是由4个大小相同的小立方块搭成的几何体,从正面和从左面看得到的形状图相同的是( )A、 B、
B、 C、
C、 D、
D、 13. 如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面.(填字母)
13. 如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面.(填字母) 14. 如图是一个正方体的展开图,标注了字母A的面是正方体的正面 , 如果正方体的左面与右面所标注式子的值相等,则x的值为 .
14. 如图是一个正方体的展开图,标注了字母A的面是正方体的正面 , 如果正方体的左面与右面所标注式子的值相等,则x的值为 . 15. 甲、乙两根木杆竖直立在平地上,其高度分别是2m和3m.某一时刻,甲木杆在太阳光下的影长为3m,则乙木杆的影长为m.16. 圆锥的侧面积为 , 底面圆半径为3cm.则圆锥的母线长为cm.
15. 甲、乙两根木杆竖直立在平地上,其高度分别是2m和3m.某一时刻,甲木杆在太阳光下的影长为3m,则乙木杆的影长为m.16. 圆锥的侧面积为 , 底面圆半径为3cm.则圆锥的母线长为cm.三、综合题
-
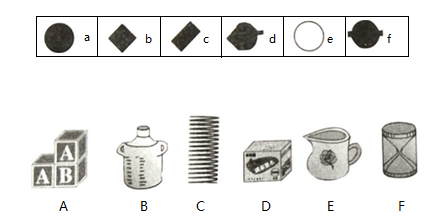
17. 如图,从上往下看 , , , , , 六个物体,分别能得到 , , , , , 哪个图形?把上下两种对应的图形于物体连接起来.
 18. 请从正面、左面、上面观察, 画出该几何体的三视图
18. 请从正面、左面、上面观察, 画出该几何体的三视图



从正面看 从左面看 从上面看
19. 一个物体由几个相同的正方体堆叠成,从三个不同方向观察得到的图形如图所示,试回答下面的问题: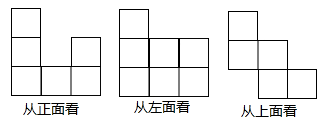 (1)、该物体共有几层?(2)、一共需要几个正方体叠成?20. 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6 m的小明落在地面上的影长为BC=2.4 m.
(1)、该物体共有几层?(2)、一共需要几个正方体叠成?20. 如图,小明与同学合作利用太阳光线测量旗杆的高度,身高1.6 m的小明落在地面上的影长为BC=2.4 m. (1)、请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;(2)、若小明测得此刻旗杆落在地面的影长EG=16 m , 请求出旗杆DE的高度.21. 某几何体的三视图如图所示,已知在△EFG中,FG=18cm,EG=12cm,∠EGF=30°;在矩形ABCD中,AD=16cm.
(1)、请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG;(2)、若小明测得此刻旗杆落在地面的影长EG=16 m , 请求出旗杆DE的高度.21. 某几何体的三视图如图所示,已知在△EFG中,FG=18cm,EG=12cm,∠EGF=30°;在矩形ABCD中,AD=16cm. (1)、请根据三视图说明这个几何体的形状.(2)、请你求出AB的长;(3)、求出该几何体的体积.22. 已知如图,扇形AOB的圆心角为120°,半径OA为9cm.
(1)、请根据三视图说明这个几何体的形状.(2)、请你求出AB的长;(3)、求出该几何体的体积.22. 已知如图,扇形AOB的圆心角为120°,半径OA为9cm. (1)、求扇形AOB的弧长和扇形面积;(2)、若把扇形纸片AOB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.23.(1)、如图所示的长方体,长、宽、高分别为4,3,6.若将它的表面沿某些棱剪开,展成一个平面图形,则下列图形中,可能是该长方体表面展开图的有(填序号).
(1)、求扇形AOB的弧长和扇形面积;(2)、若把扇形纸片AOB卷成一个圆锥形无底纸帽,求这个纸帽的高OH.23.(1)、如图所示的长方体,长、宽、高分别为4,3,6.若将它的表面沿某些棱剪开,展成一个平面图形,则下列图形中,可能是该长方体表面展开图的有(填序号).
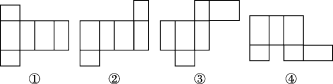 (2)、图A,B分别是题(1)中长方体的两种表面展开图,求得图A的外围周长为52,请你求出图B的外围周长.
(2)、图A,B分别是题(1)中长方体的两种表面展开图,求得图A的外围周长为52,请你求出图B的外围周长. (3)、第(1)题中长方体的表面展开图还有不少,聪明的你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.24. 某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时点A,C,E三点共线.
(3)、第(1)题中长方体的表面展开图还有不少,聪明的你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.24. 某兴趣小组开展课外活动.如图,小明从点M出发以1.5米/秒的速度,沿射线MN方向匀速前进,2秒后到达点B,此时他(AB)在某一灯光下的影长为MB,继续按原速行走2秒到达点D,此时他(CD)在同一灯光下的影子GD仍落在其身后,并测得这个影长GD为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点F,此时点A,C,E三点共线. (1)、请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影长FH(不写画法);(2)、求小明到达点F时的影长FH的长.
(1)、请在图中画出光源O点的位置,并画出小明位于点F时在这个灯光下的影长FH(不写画法);(2)、求小明到达点F时的影长FH的长.