浙江省湖州市吴兴区2020-2021学年七年级下学期期中数学试卷
试卷更新日期:2022-03-25 类型:期中考试
一、单选题
-
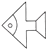
1. 将如图所示的图案通过平移后可以得到的图案是( )
 A、
A、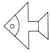 B、
B、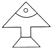 C、
C、 D、
D、 2. 下列是二元一次方程的是( )A、 B、 C、 D、3. 在下列代数式中,次数为3的单项式是( )A、xy2 B、x3+y3 C、x3y D、3xy4. 计算 的结果是( )A、 B、 C、 D、5. 要使等式(x-2y)2+A=(x+2y)2成立,代数式A应是( )A、4xy B、-4xy C、8xy D、-8xy6. 已知 ,则a+b等于( )A、2 B、 C、3 D、17. 如果 的乘积中不含 的一次项,则 的值为( )A、 B、2 C、 D、0.58. 小明同学把一个含有45°角的直角三角板在如图所示的两条平行线 m、n 上,测得 ,则 的度数是( )
2. 下列是二元一次方程的是( )A、 B、 C、 D、3. 在下列代数式中,次数为3的单项式是( )A、xy2 B、x3+y3 C、x3y D、3xy4. 计算 的结果是( )A、 B、 C、 D、5. 要使等式(x-2y)2+A=(x+2y)2成立,代数式A应是( )A、4xy B、-4xy C、8xy D、-8xy6. 已知 ,则a+b等于( )A、2 B、 C、3 D、17. 如果 的乘积中不含 的一次项,则 的值为( )A、 B、2 C、 D、0.58. 小明同学把一个含有45°角的直角三角板在如图所示的两条平行线 m、n 上,测得 ,则 的度数是( )
A、45° B、55° C、65° D、75°9. 下列说法错误的个数是( )①经过一点有且只有一条直线与已知直线平行;
②垂直于同一条直线的两条直线互相平行;
③直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
④同一平面内不相交的两条直线叫做平行线.
A、1个 B、2个 C、3个 D、4个10. 矩形 内放入两张边长分别为 和 的正方纸片,按照图①放置,矩形纸片没有两个正方形覆盖的部分(黑色阴影部分)的面积为 ;按照图②放置,矩形纸片没有被两个正方形覆盖的部分面积为 ;按图③放置,矩形纸片没有被两个正方形覆盖的部分的面积为 .已知 , ,设 ,则下列值是常数的是( )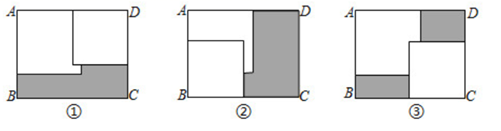 A、 B、 C、 D、a+b
A、 B、 C、 D、a+b二、填空题
-
11. 因式分解: .12. 用科学记数法表示: .13. 若 , ,则 的值是.14. 若 与 的两边分别平行,且 , ,则 的度数为.15. 老师有 个礼物(其中 ,且n为整数).现在将这些礼物平均分给班级的同学,恰好能分完,那么下列选项中:①4个;②12个;③ 个;④ 个,可以是班级的同学个数的是.16. 定义一种新的运算: ,例如: ,那么(1)、若 ,那么 ;(2)、若 ,且关于x,y的二元一次方程 ,当a,b取不同值时,方程都有一个公共解,那么公共解为.
三、解答题
-
17. 计算:18. 解方程(组):(1)、(2)、19. 先化简,再求值: ,其中 .20. 如图,在每个小正方形边长为1方格纸中, 的顶点都在方格纸格点上.将 向左平移2格,再向上平移4格.
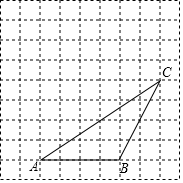 (1)、请在图中画出平移后的 ;(2)、再在图中画出 的高 ,并求出 在整个平移过程中线段 扫过的面积.21. 如图,已知点 , 在直线 上, , , .
(1)、请在图中画出平移后的 ;(2)、再在图中画出 的高 ,并求出 在整个平移过程中线段 扫过的面积.21. 如图,已知点 , 在直线 上, , , . (1)、求 的度数;(2)、若 平分 ,交 于点 ,且 ,求 的度数.22. 随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆 型汽车、3辆 型汽车的进价共计80万元;3辆 型汽车、2辆 型汽车的进价共计95万元.(1)、求 、 两种型号的汽车每辆进价分别为多少万元?(2)、若该公司计划正好用180万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案.23. 实验材料:现有若干块如图①所示的正方形和长方形硬纸片.实验目的:用若干块这样的正方形和长方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,得到相应的等式,从而探求出多项式乘法或分解因式的新途径.例如,选取正方形、长方形硬纸片共6块,拼出一个如图②的长方形,计算它的面积写出相应的等式有 或 .
(1)、求 的度数;(2)、若 平分 ,交 于点 ,且 ,求 的度数.22. 随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆 型汽车、3辆 型汽车的进价共计80万元;3辆 型汽车、2辆 型汽车的进价共计95万元.(1)、求 、 两种型号的汽车每辆进价分别为多少万元?(2)、若该公司计划正好用180万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案.23. 实验材料:现有若干块如图①所示的正方形和长方形硬纸片.实验目的:用若干块这样的正方形和长方形硬纸片拼成一个新的长方形,通过不同的方法计算面积,得到相应的等式,从而探求出多项式乘法或分解因式的新途径.例如,选取正方形、长方形硬纸片共6块,拼出一个如图②的长方形,计算它的面积写出相应的等式有 或 .
探索问题:
(1)、选取图①所示的正方形、长方形硬纸片共8块可以拼出一个如图②的长方形,计算图②的面积,并写出相应的等式;(2)、试借助拼图的方法,把二次三项式 分解因式,并把所拼的图形画在方框内.(3)、小明同学又用了 张边长为 的正方形, 张边长为 的正方形, 张边长为 , 的长方形纸片拼出了一个面积为 的长方形,那么 的值为.24. 已知 , 平面内一点, 于 . (1)、如图1,直接写出 和 之间的数量关系;(2)、如图2,过点 作 于点 ,求证: ;(3)、如图3,在(2)问的条件下,点 、 在 上,连接 , , , 平分 , 平分 ,若 , ,求 的度数.
(1)、如图1,直接写出 和 之间的数量关系;(2)、如图2,过点 作 于点 ,求证: ;(3)、如图3,在(2)问的条件下,点 、 在 上,连接 , , , 平分 , 平分 ,若 , ,求 的度数.