浙江省杭州市萧山区城北片2020-2021学年七年级下学期期中数学试卷
试卷更新日期:2022-03-25 类型:期中考试
一、单选题
-
1. 下列是二元一次方程的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、 C、 D、3. 如图为一只小兔,将图进行平移,得到的图形可能是下列选项中的( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 若 , ,则 ( )A、 B、 C、 D、5. 对于① ,② ,从左到右的变形,表述正确的是( )A、都是因式分解 B、都是乘法运算 C、①是因式分解,②是乘法运算 D、①是乘法运算,②是因式分解6. 下列说法错误的是( )A、平面内过一点有且只有一条直线与已知直线平行 B、平面内过一点有且只有一条直线与已知直线垂直 C、两点之间的所有连线中,线段最短 D、对顶角相等7. 如图,已知直线 .直角三角板 的直角顶点C在直线b上,若 ,则 ( )
4. 若 , ,则 ( )A、 B、 C、 D、5. 对于① ,② ,从左到右的变形,表述正确的是( )A、都是因式分解 B、都是乘法运算 C、①是因式分解,②是乘法运算 D、①是乘法运算,②是因式分解6. 下列说法错误的是( )A、平面内过一点有且只有一条直线与已知直线平行 B、平面内过一点有且只有一条直线与已知直线垂直 C、两点之间的所有连线中,线段最短 D、对顶角相等7. 如图,已知直线 .直角三角板 的直角顶点C在直线b上,若 ,则 ( ) A、 B、 C、 D、8. 下列各式中能用平方差公式的是( )A、(a+b)(b+a) B、(a+b)(﹣b﹣a) C、(a+b)(b﹣a) D、(﹣a+b)(b﹣a)9. 我们知道下面的结论:若 ( ,且 ),则 .利用这个结论解决下列问题:设 , , ,下列关系式正确的是( )A、 B、 C、 D、10. 利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.量的数据如图,则桌子的高度等于( )
A、 B、 C、 D、8. 下列各式中能用平方差公式的是( )A、(a+b)(b+a) B、(a+b)(﹣b﹣a) C、(a+b)(b﹣a) D、(﹣a+b)(b﹣a)9. 我们知道下面的结论:若 ( ,且 ),则 .利用这个结论解决下列问题:设 , , ,下列关系式正确的是( )A、 B、 C、 D、10. 利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.量的数据如图,则桌子的高度等于( )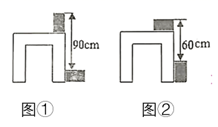 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
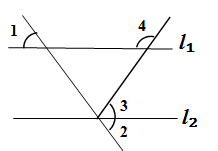
11. 因式分解: .12. 已知 是二元一次方程7x+2y=10的一组解,则m的值是.13. 若 是完全平方式.则 的值是.14. 已知:如图, ,则∠4的度数是.
 15. 一个长方形花园,长为a , 宽为b , 中间有两条互相垂直的宽为c的路,则可种花的面积为 .
15. 一个长方形花园,长为a , 宽为b , 中间有两条互相垂直的宽为c的路,则可种花的面积为 . 16. 如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是.
16. 如图,大正方形与小正方形的面积之差是60,则阴影部分的面积是.
三、解答题
-
17.(1)、解下列方程组 .(2)、因式分解 .18.(1)、填空:
① =;
② = .
(2)、先化简,再求值: ,其中 .19. 如图, , . (1)、求证: ;(2)、若DG是 的角平分线, ,求 的度数.20. 某中学为了响应“足球进校园”的号召,在商场购买 、 两种品牌的足球,已知购买一个 品牌足球比购买一个 品牌足球多30元,购买2个 品牌足球和3个 品牌足球共需340元.(1)、求购买一个 品牌足球和一个 品牌足球各需多少元?(2)、该中学决定购买 、 两种品牌足球共50个,恰商场对两种品牌足球的售价进行调整, 品牌足球售价比原来提高 , 品牌足球按原售价的九折出售,如果此次购买 、 两种品牌足球总费用为3060元,那么该中学购进 品牌足球多少个?21. 下面是某同学对多项式 因式分解的过程.
(1)、求证: ;(2)、若DG是 的角平分线, ,求 的度数.20. 某中学为了响应“足球进校园”的号召,在商场购买 、 两种品牌的足球,已知购买一个 品牌足球比购买一个 品牌足球多30元,购买2个 品牌足球和3个 品牌足球共需340元.(1)、求购买一个 品牌足球和一个 品牌足球各需多少元?(2)、该中学决定购买 、 两种品牌足球共50个,恰商场对两种品牌足球的售价进行调整, 品牌足球售价比原来提高 , 品牌足球按原售价的九折出售,如果此次购买 、 两种品牌足球总费用为3060元,那么该中学购进 品牌足球多少个?21. 下面是某同学对多项式 因式分解的过程.解:设 ,
则原式 (第一步)
(第二步)
(第三步)
(第四步)
解答下列问题:
(1)、该同学第二步到第三步运用了因式分解的方法是( )A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式(2)、该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果.(3)、请你模仿以上方法尝试对多项式 进行因式分解.

