重庆市缙云教育联盟2022年中考第一次适应性测试数学试卷
试卷更新日期:2022-03-25 类型:中考模拟
一、单选题
-
1. 四个有理数-3、-1、0、1,其中最小的是( )A、-3 B、-1 C、0 D、12. 下列各式运算正确的是( )A、 B、 C、 D、3. 如图的一个几何体,其左视图是( )
 A、
A、 B、
B、 C、
C、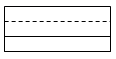 D、
D、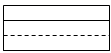 4. 在平面直角坐标系中,将点A(-1,2)向下平移3个单位长度,再向右平移2个单位长度,得到点A′,则点A′的坐标是( )A、(-3,-1) B、(1,-1) C、(-1,1) D、(-4,4)5. 下列调查中,适合抽样调查的是( ).A、调查本班同学的体育达标情况 B、了解“嫦娥五号”探测器的零部件状况 C、疫情期间,了解全校师生入校时体温情况 D、调查黄河的水质情况6. 如图,与位似,点是它们的位似中心,其中 , 则与的面积之比是( )
4. 在平面直角坐标系中,将点A(-1,2)向下平移3个单位长度,再向右平移2个单位长度,得到点A′,则点A′的坐标是( )A、(-3,-1) B、(1,-1) C、(-1,1) D、(-4,4)5. 下列调查中,适合抽样调查的是( ).A、调查本班同学的体育达标情况 B、了解“嫦娥五号”探测器的零部件状况 C、疫情期间,了解全校师生入校时体温情况 D、调查黄河的水质情况6. 如图,与位似,点是它们的位似中心,其中 , 则与的面积之比是( )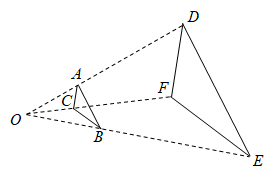 A、 B、 C、 D、1:97. 如图,第①个图形中共有4个小黑点,第②个图形中共有7个小黑点,第③个图形中共有10个小黑点,第④个图形中共有13个小黑点,……,按此规律排列下去,则第⑥个图形中小黑点的个数为( )
A、 B、 C、 D、1:97. 如图,第①个图形中共有4个小黑点,第②个图形中共有7个小黑点,第③个图形中共有10个小黑点,第④个图形中共有13个小黑点,……,按此规律排列下去,则第⑥个图形中小黑点的个数为( ) A、19 B、20 C、22 D、258. 的边 经过圆心O, 与圆相切于点A,若 ,则 的大小等于( )
A、19 B、20 C、22 D、258. 的边 经过圆心O, 与圆相切于点A,若 ,则 的大小等于( ) A、 B、 C、 D、9. 勾股定理是人类早期发现并证明的重要数学定理之一,是数形结合的重要纽带.数学家欧几里得利用如图验证了勾股定理:以直角三角形ABC的三条边为边长向外作正方形ACHI,正方形ABED,正方形BCGF,连接BI,CD,过点C作CJ⊥DE于点J,交AB于点K.设正方形ACHI的面积为S1 , 正方形BCGF的面积为S2 , 长方形AKJD的面积为S3 , 长方形KJEB的面积为S4 , 下列结论:①BI=CD;②2S△ACD=S1;③S1+S4=S2+S3;④ + = .其中正确的结论有( )
A、 B、 C、 D、9. 勾股定理是人类早期发现并证明的重要数学定理之一,是数形结合的重要纽带.数学家欧几里得利用如图验证了勾股定理:以直角三角形ABC的三条边为边长向外作正方形ACHI,正方形ABED,正方形BCGF,连接BI,CD,过点C作CJ⊥DE于点J,交AB于点K.设正方形ACHI的面积为S1 , 正方形BCGF的面积为S2 , 长方形AKJD的面积为S3 , 长方形KJEB的面积为S4 , 下列结论:①BI=CD;②2S△ACD=S1;③S1+S4=S2+S3;④ + = .其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个10. 在平面直角坐标系中,将点 先向左平移 个单位得点 ,再将 向上平移 个单位得点 ,若点 落在第三象限,则a的取值范围是( )A、 B、 C、 D、 或11. 如图,在平面直角坐标系中,菱形 的边 在x轴的正半轴上,反比例函数 的图象经过对角线 的中点D和顶点C若菱形 的面积为9,则k的值为( )
A、1个 B、2个 C、3个 D、4个10. 在平面直角坐标系中,将点 先向左平移 个单位得点 ,再将 向上平移 个单位得点 ,若点 落在第三象限,则a的取值范围是( )A、 B、 C、 D、 或11. 如图,在平面直角坐标系中,菱形 的边 在x轴的正半轴上,反比例函数 的图象经过对角线 的中点D和顶点C若菱形 的面积为9,则k的值为( ) A、 B、 C、 D、12. 如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD , AE相交于F , 已知BD=4AD , 设△ABC的面积为S , △CEF的面积为S1 , △ADF的面积为S2 , 则 的值为( )
A、 B、 C、 D、12. 如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD , AE相交于F , 已知BD=4AD , 设△ABC的面积为S , △CEF的面积为S1 , △ADF的面积为S2 , 则 的值为( )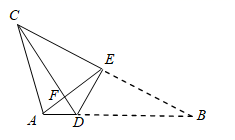 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若x|m|﹣10=2是关于x的一元一次方程,则m的值是 .14. 据中国电影数据信息网消息,截止到 年 月 日,诠释伟大抗美援朝精神的电影 长津湖 累计票房已达 亿元.将 亿元用科学记数法表示元.15. 如图,已知 ,外心为 , , ,分别以 , 为腰向形外作等腰直角三角形 与 ,连接 , 交于点P,则 的最小值是.
 16. 一个不透明的袋中共有5个小球,分别为2个红球和3个黄球,它们除颜色外完全相同,随机摸出两个小球,则摸出两个颜色不同小球的概率是 .
16. 一个不透明的袋中共有5个小球,分别为2个红球和3个黄球,它们除颜色外完全相同,随机摸出两个小球,则摸出两个颜色不同小球的概率是 .三、解答题
-
17. 计算题(1)、(2)、18. 某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了 箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩计算了甲成绩的平均数和方差(见小宇的作业).

第 次
第 次
第 次
第 次
第 次
甲成绩
乙成绩
(1)、求a和乙的方差 ;(2)、请你从平均数和方差的角度分析,谁将被选中.19. 阅读理解:若x满足 ,求 的值.
解:设 , ,
则 , ,
.
迁移应用:
(1)、若x满足 ,求 的值;(2)、如图,点E,G分别是正方形 的边 、 上的点,满足 , 为常数,且 ,长方形 的面积是 ,分别以 、 作正方形 和正方形 ,求阴影部分的面积. 20. 如图,在平面直角坐标系 中,已知反比例函数 的图象经过点为A(-2,m).过点A作AB⊥x轴,且 ABO的面积为2.
20. 如图,在平面直角坐标系 中,已知反比例函数 的图象经过点为A(-2,m).过点A作AB⊥x轴,且 ABO的面积为2. (1)、k和m的值;(2)、若点C(x,y)也在反比例函数 的图象上,当 时,直接写出函数值y的取值范围.21. 已知二次函数 的图象经过点 ,对称轴是经过 且平行于y轴的直线.
(1)、k和m的值;(2)、若点C(x,y)也在反比例函数 的图象上,当 时,直接写出函数值y的取值范围.21. 已知二次函数 的图象经过点 ,对称轴是经过 且平行于y轴的直线. (1)、求m,n的值,(2)、如图,一次函数 的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,若点B与点 关于抛物线对称轴对称,求一次函数的表达式.(3)、根据函数图象直接写出 时,x的取值范围.22. 在平面直角坐标系 中,点A是抛物线 的顶点.
(1)、求m,n的值,(2)、如图,一次函数 的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,若点B与点 关于抛物线对称轴对称,求一次函数的表达式.(3)、根据函数图象直接写出 时,x的取值范围.22. 在平面直角坐标系 中,点A是抛物线 的顶点. (1)、求点A的坐标(用含m的代数式表示);(2)、若射线 与x轴所成的锐角为 ,求m的值;(3)、将点 向左平移 个单位得到点Q,若抛物线与线段 只有一个公共点,直接写出m的取值范围.23. 在 中, ,点O是斜边 上的一点,连接 ,点D是 上一点,过点D分别作 , ,交 于点E、F.(1)、如图1,若点O为斜边 的中点,求证:点O是线段 的中点.
(1)、求点A的坐标(用含m的代数式表示);(2)、若射线 与x轴所成的锐角为 ,求m的值;(3)、将点 向左平移 个单位得到点Q,若抛物线与线段 只有一个公共点,直接写出m的取值范围.23. 在 中, ,点O是斜边 上的一点,连接 ,点D是 上一点,过点D分别作 , ,交 于点E、F.(1)、如图1,若点O为斜边 的中点,求证:点O是线段 的中点. (2)、如图2,在(1)的条件下,将 绕点O顺时针旋转任意一个角度,连接 , ,请写出线段 和线段 的数量关系,并说明理由.
(2)、如图2,在(1)的条件下,将 绕点O顺时针旋转任意一个角度,连接 , ,请写出线段 和线段 的数量关系,并说明理由. (3)、如图3,若点O是斜边 的三等分点,且靠近点 ,当 时,将 绕点O顺时针旋转任意一个角度,连接 、 、 ,请求出 的值.
(3)、如图3,若点O是斜边 的三等分点,且靠近点 ,当 时,将 绕点O顺时针旋转任意一个角度,连接 、 、 ,请求出 的值.