湖北省武汉市洪山区华中师大一附中光谷分校2021年中考数学模拟试卷
试卷更新日期:2022-03-25 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. 袋子中装有2个黑球和1个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,下列事件中是必然事件的是( )A、摸出的2个球中有1个球是白球 B、摸出的2个球中至少有1个球是黑球 C、摸出的2个球都是黑球 D、摸出的2个球都是白球3. 下面是科学防控新冠知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列几何体是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )A、
4. 下列几何体是由4个相同的小正方体搭成的,其中,主视图、左视图、俯视图都相同的是( )A、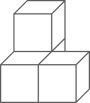 B、
B、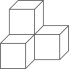 C、
C、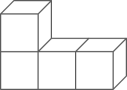 D、
D、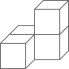 5. 计算(﹣2x2)4的结果是( )A、8x6 B、﹣8x8 C、﹣16x8 D、16x86. 布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出第二个球,两次都摸出白球的概率是( )A、 B、 C、 D、7. 已知反比例函数 ,当|y|≥3时,x的取值范围是( )A、x≥2或x≤﹣2 B、﹣2≤x≤2 C、0<x≤2或x≤﹣2 D、﹣2≤x<0或0<x≤28. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )
5. 计算(﹣2x2)4的结果是( )A、8x6 B、﹣8x8 C、﹣16x8 D、16x86. 布袋中装有除颜色外没有其他区别的1个红球和2个白球,搅匀后从中摸出一个球,放回搅匀,再摸出第二个球,两次都摸出白球的概率是( )A、 B、 C、 D、7. 已知反比例函数 ,当|y|≥3时,x的取值范围是( )A、x≥2或x≤﹣2 B、﹣2≤x≤2 C、0<x≤2或x≤﹣2 D、﹣2≤x<0或0<x≤28. 如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( ) A、 B、2 C、 D、29. 如图,AB和CD是⊙O的两条互相垂直的弦,若AD=4,BC=2,则阴影部分的面积是( )
A、 B、2 C、 D、29. 如图,AB和CD是⊙O的两条互相垂直的弦,若AD=4,BC=2,则阴影部分的面积是( ) A、2π﹣1 B、 π﹣4 C、5π﹣4 D、5π﹣810. 如图,直线y=x+8分别交x、y轴于A、B两点,交双曲线 ,若CD=3(AC+BD),则k的值为( )
A、2π﹣1 B、 π﹣4 C、5π﹣4 D、5π﹣810. 如图,直线y=x+8分别交x、y轴于A、B两点,交双曲线 ,若CD=3(AC+BD),则k的值为( ) A、﹣6 B、﹣7 C、﹣8 D、﹣9
A、﹣6 B、﹣7 C、﹣8 D、﹣9二、填空题
-
11. 计算 的结果是12. 某中学组织全校师生迎“五四”诗词大赛,25名参赛同学的得分情况如图所示,这些成绩的中位数是 , 众数是.
 13. 方程 +3= 的解是.14. 如图,海上有一灯塔P,位于小岛A北偏东60°方向上,由西向东航行24nmile到达B处,这时测得灯塔P在北偏东30°方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P的正南方,此时轮船与灯塔P的距离是nmile.(结果保留一位小数, ≈1.73)
13. 方程 +3= 的解是.14. 如图,海上有一灯塔P,位于小岛A北偏东60°方向上,由西向东航行24nmile到达B处,这时测得灯塔P在北偏东30°方向上,如果轮船不改变航向继续向东航行,当轮船到达灯塔P的正南方,此时轮船与灯塔P的距离是nmile.(结果保留一位小数, ≈1.73) 15. 抛物线y=ax2+bx+c(a,b,c是常数,a<0)的顶点坐标为(1,m),其中m>0.下列四个结论:
15. 抛物线y=ax2+bx+c(a,b,c是常数,a<0)的顶点坐标为(1,m),其中m>0.下列四个结论:①ab<0;
②c>0;
③关于x的一元二次方程ax2﹣bx+c=m+1无实数解;
④点P1(n,y1),P2(3﹣2n,y2)在抛物线上,若n<1,则y1<y2.
其中正确的结论是(填写序号).
16. 如图,在△ABD中,∠ADB=90°,AB=8,C是AB中点,E是BD中点,将点E绕B点顺时针旋转90°为点F,则CF的最小值为 .
三、解答题
-
17. 不等式组 请按下列步骤完成解答:(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来;
 (4)、原不等式组的解集为18. 已知:如图,D,E,F分别是AB,AC,BC上的点,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2.
(4)、原不等式组的解集为18. 已知:如图,D,E,F分别是AB,AC,BC上的点,DE∥BC,∠ADE=∠EFC,求证:∠1=∠2. 19. 某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:
19. 某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下: (1)、直接写出这次抽取的样本的容量为 ;(2)、请在图2中把条形统计图补充完整.(3)、已知该校这次活动共收到参赛作品800份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?20. 如图,△ABC的顶点均为格点,AC与网格线交于点D.仅用无刻度尺的直尺在网格中画图,画图过程用虚线表示,画图结果用实线表示.
(1)、直接写出这次抽取的样本的容量为 ;(2)、请在图2中把条形统计图补充完整.(3)、已知该校这次活动共收到参赛作品800份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?20. 如图,△ABC的顶点均为格点,AC与网格线交于点D.仅用无刻度尺的直尺在网格中画图,画图过程用虚线表示,画图结果用实线表示. (1)、如图1,画出△ABC的角平分线CE;(2)、如图1,平移AB至DN,使点A的对应点为点D;(3)、如图2,在AB上找一点G,使DG+CG最小;(4)、如图3,AB与网格线交于点E,过点E作EQ⊥AC于Q.21. 如图1,已知AB是⊙O的直径,C,D为⊙O上的点,BD平分∠ABC,过D作DP⊥BC交BC的延长线于点P.
(1)、如图1,画出△ABC的角平分线CE;(2)、如图1,平移AB至DN,使点A的对应点为点D;(3)、如图2,在AB上找一点G,使DG+CG最小;(4)、如图3,AB与网格线交于点E,过点E作EQ⊥AC于Q.21. 如图1,已知AB是⊙O的直径,C,D为⊙O上的点,BD平分∠ABC,过D作DP⊥BC交BC的延长线于点P. (1)、求证:DP是⊙O的切线.(2)、如图2,若E是OB的中点,EF⊥OB交直线DP于点F,EF= ,tan∠ABD= ,求⊙O的半径.22. 某公司投入研发费用120万元(120万元只计入第一年成本),成功研发出一种产品,产品正式投产后,生产成本为8元/件.经试销发现年销售量y(万件)与售价x(元/件)有如表对应关系.
(1)、求证:DP是⊙O的切线.(2)、如图2,若E是OB的中点,EF⊥OB交直线DP于点F,EF= ,tan∠ABD= ,求⊙O的半径.22. 某公司投入研发费用120万元(120万元只计入第一年成本),成功研发出一种产品,产品正式投产后,生产成本为8元/件.经试销发现年销售量y(万件)与售价x(元/件)有如表对应关系.x(元/件)
1
3
5
y(万件)
39
37
35
(1)、直接写出y关于x的函数关系式:.(2)、若物价部门规定每件商品的利润率不得超过150%,当第一年的产品的售价x为多少时,年利润W最大,其最大值是多少?(3)、为了提高利润,第二年该公司将第一年的最大利润再次投入研发(此费用计入第二年成本),使产品的生产成本降为5元/件,但规定第二年产品的售价涨幅不能超过第一年售价的20%,在年销售量y(万件)与售价x(元/件)的函数关系不变的情况下,若公司要求第二年的利润不低于166万元,求该公司第二年售价x(元/件)应满足的条件.23. 如图1,在四边形ABCD中,AB∥CD,AC、BD相交于点P, .
(1)、求证:∠BAC=∠CBD;(2)、如图2,E,F分别为边AD、BC上的点,PE DC, ,①求证:∠PFC=∠CPD;
②若BP=2,PD=1,锐角∠BCD的正弦值为 ,直接写出BF的长.
24. 已知抛物线y= . (1)、如图1,当c=﹣6时,抛物线分别交x轴于A,B,交y轴于点C.
(1)、如图1,当c=﹣6时,抛物线分别交x轴于A,B,交y轴于点C.①直接写出直线CB的解析式;
②点P在直线BC下方抛物线上,作PD y轴,交线段BC于点D,作PE x轴,交抛物线于另一点E,若PE=PD,求点P的坐标;
(2)、如图2,若抛物线与x轴有唯一公共点F,直线l:y=kx+b(k>0,b>0)与抛物线交于M,N两点(点N在点M右边),直线MG⊥x轴,交直线NF于点G,且点G的纵坐标为-3,求证:直线l过定点.