湖北省潜江市2021年中考数学模拟试卷(5月份)
试卷更新日期:2022-03-25 类型:中考模拟
一、选择题
-
1. 下列实数是无理数的是( )A、-2 B、 C、 D、2. 近几年来,我国经济规模不断扩大,综合国力显著增强.2019年我国国内生产总值约991000亿元,则数991000用科学记数法可表示为( )A、991×103 B、99.1×104 C、9.91×105 D、9.91×1063. 某物体如图所示,它的主视图是( )
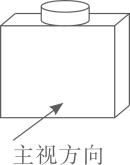 A、
A、 B、
B、 C、
C、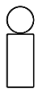 D、
D、 4. 冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,11,13,15.关于这组数据,冉冉得出如下结果,错误的是( )A、众数是11 B、平均数是12 C、方差是 D、中位数是135. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1的度数为( )
4. 冉冉的妈妈在网上销售装饰品.最近一周,每天销售某种装饰品的个数为:11,10,11,13,11,13,15.关于这组数据,冉冉得出如下结果,错误的是( )A、众数是11 B、平均数是12 C、方差是 D、中位数是135. 如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=37°时,∠1的度数为( ) A、37° B、43° C、53° D、54°6. 若关于x的分式方程 = +5的解为正数,则m的取值范围为( )A、m<﹣10 B、m≤﹣10 C、m≥﹣10且m≠﹣6 D、m>﹣10且m≠﹣67. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根8. 如图,双曲线 (x<0)经过▱ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则▱OABC的面积是( )
A、37° B、43° C、53° D、54°6. 若关于x的分式方程 = +5的解为正数,则m的取值范围为( )A、m<﹣10 B、m≤﹣10 C、m≥﹣10且m≠﹣6 D、m>﹣10且m≠﹣67. 关于x的方程 ( 为常数)根的情况下,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根8. 如图,双曲线 (x<0)经过▱ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则▱OABC的面积是( )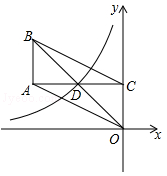 A、 B、 C、3 D、69. 在平面直角坐标系中,点O为坐标原点,抛物线y= ﹣2x﹣3与y轴交于点A,与x轴正半轴交于点B,连接AB,将Rt△OAB向右上方平移,得到Rt△O'A'B',且点 ,点 落在抛物线的对称轴上,点 落在抛物线上,则直线 的表达式为( )A、y=x B、y=x+1 C、y=x+ D、y=x+210. 如图,在正方形ABCD中,点E是边BC的中点,连接AE、DE , 分别交BD、AC于点P、Q , 过点P作PF⊥AE交CB的延长线于F , 下列结论:
A、 B、 C、3 D、69. 在平面直角坐标系中,点O为坐标原点,抛物线y= ﹣2x﹣3与y轴交于点A,与x轴正半轴交于点B,连接AB,将Rt△OAB向右上方平移,得到Rt△O'A'B',且点 ,点 落在抛物线的对称轴上,点 落在抛物线上,则直线 的表达式为( )A、y=x B、y=x+1 C、y=x+ D、y=x+210. 如图,在正方形ABCD中,点E是边BC的中点,连接AE、DE , 分别交BD、AC于点P、Q , 过点P作PF⊥AE交CB的延长线于F , 下列结论:①∠AED+∠EAC+∠EDB=90°,②AP=FP , ③AE= AO , ④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36,⑤CE•EF=EQ•DE .
其中正确的结论有( )
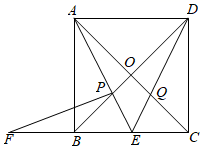 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
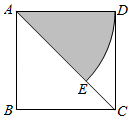
11. 多项式 分解因式的结果是.12. 如图,正方形ABCD的边长为4,以点A为圆心,画圆弧DE得到扇形ADE(阴影部分,点E在对角线AC上).若扇形ADE正好是一个圆锥的侧面展开图,则该圆锥的底面圆的半径为.
 13. 某校九(1)班准备举行一次演讲比赛,甲、乙、丙三人通过抽签方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是.14. 学校计划用200元钱购买A、B两种奖品,A种每个15元,B种每个25元,有 种购买方案.15. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是米.
13. 某校九(1)班准备举行一次演讲比赛,甲、乙、丙三人通过抽签方式决定出场顺序,则出场顺序恰好是甲、乙、丙的概率是.14. 学校计划用200元钱购买A、B两种奖品,A种每个15元,B种每个25元,有 种购买方案.15. 如图,小明在距离地面30米的P处测得A处的俯角为15°,B处的俯角为60°.若斜面坡度为1: ,则斜坡AB的长是米. 16. 如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y= x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y= x于点B3 , …,按照此规律进行下去,则点An的横坐标为 .
16. 如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y= x于点B1 , B2 , 过点B2作y轴的平行线交直线y=x于点A2 , 过点A2作x轴的平行线交直线y= x于点B3 , …,按照此规律进行下去,则点An的横坐标为 .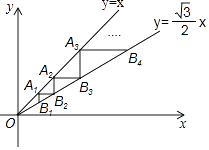
三、解答题
-
17.(1)、计算:(﹣2)2﹣| |﹣2cos45°+(2020﹣π)0;(2)、解不等式组: .18. 按要求作图,不要求写作法,但要保留作图痕迹.只用直尺(不带刻度)
 (1)、如图1,如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上,请在这个网格中作线段AB的垂直平分线;(2)、如图2,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH.19. 某校为了解本校九年级学生足球训练情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为4个等级:A、B、C、D,并将统计结果绘制成两幅不完整的统计图.
(1)、如图1,如图,在5×5的正方形网格中有一条线段AB,点A与点B均在格点上,请在这个网格中作线段AB的垂直平分线;(2)、如图2,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH.19. 某校为了解本校九年级学生足球训练情况,随机抽查该年级若干名学生进行测试,然后把测试结果分为4个等级:A、B、C、D,并将统计结果绘制成两幅不完整的统计图.
请根据图中的信息解答下列问题
(1)、补全条形统计图(2)、该年级共有700人,估计该年级足球测试成绩为D等的人数为人;(3)、在此次测试中,有甲、乙、丙、丁四个班的学生表现突出,现决定从这四个班中随机选取两个班在全校举行一场足球友谊赛.请用画树状图或列表的方法,求恰好选到甲、乙两个班的概率.20. 如图,直线y=3x与双曲线y= (k≠0,且x>0)交于点A,点A的横坐标是1.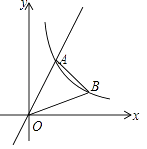 (1)、求点A的坐标及双曲线的解析式;(2)、点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.
(1)、求点A的坐标及双曲线的解析式;(2)、点B是双曲线上一点,且点B的纵坐标是1,连接OB,AB,求△AOB的面积.
21. 如图,已知AB是⊙O的直径,⊙O经过Rt△ACD的直角边DC上的点F,点F是弧EB的中点,∠C=90°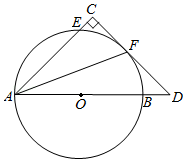 (1)、求证:直线CD是⊙O切线.(2)、若BD=2,OB=4,求tan∠AFC的值.22. 2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为 ,销售量y(千克)与x之间的关系如图所示.
(1)、求证:直线CD是⊙O切线.(2)、若BD=2,OB=4,求tan∠AFC的值.22. 2020年是决战决胜扶贫攻坚和全面建成小康社会的收官之年,荆门市政府加大各部门和单位对口扶贫力度.某单位的帮扶对象种植的农产品在某月(按30天计)的第x天(x为正整数)的销售价格p(元/千克)关于x的函数关系式为 ,销售量y(千克)与x之间的关系如图所示. (1)、求y与x之间的函数关系式,并写出x的取值范围;(2)、当月第几天,该农产品的销售额最大,最大销售额是多少?
(1)、求y与x之间的函数关系式,并写出x的取值范围;(2)、当月第几天,该农产品的销售额最大,最大销售额是多少?(销售额=销售量×销售价格)
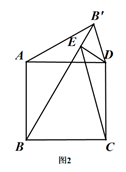
23. 将正方形 的边 绕点A逆时针旋转至 ,记旋转角为 .连接 ,过点D作 垂直于直线 ,垂足为点E,连接 ,(1)、如图1,当 时, 的形状为 ,连接 ,可求出 的值为; (2)、当 且 时,
(2)、当 且 时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点 为顶点的四边形是平行四边形时,请直接写出 的值.
 24. 如图,抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C . 直线l与抛物线交于A , D两点,与y轴交于点E , 点D的坐标为 .
24. 如图,抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C . 直线l与抛物线交于A , D两点,与y轴交于点E , 点D的坐标为 .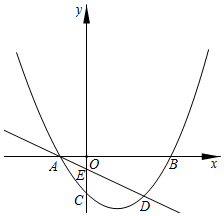 (1)、求A , B两点的坐标及直线l的函数表达式;(2)、若点P是抛物线上的点,点P的横坐标为 ,过点P作 轴,垂足为M . 与直线l交于点N , 当点N是线段 的三等分点时,求点P的坐标;(3)、若点Q是y轴上的点,且 ,求点Q的坐标.
(1)、求A , B两点的坐标及直线l的函数表达式;(2)、若点P是抛物线上的点,点P的横坐标为 ,过点P作 轴,垂足为M . 与直线l交于点N , 当点N是线段 的三等分点时,求点P的坐标;(3)、若点Q是y轴上的点,且 ,求点Q的坐标.