四川省成都市2022年九年级数学中考复习第一次综合模拟测试卷

试卷更新日期：2022-03-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列等式从左到右的变形，属于因式分解的是（　　）

A、8x² y³＝2x²⋅4 y³ B、（ x+1）（ x﹣1）＝x²﹣1 C、3x﹣3y﹣1＝3（ x﹣y）﹣1 D、x²﹣8x+16＝（ x﹣4）²

查看试题解析
2. 不等式组 ${\begin{array}{l} 5 - x > - 1 \\ 3 x \geq \frac{x - 1}{2} \end{array}$ 的所有整数解的和为（　　）

A、13 B、15 C、16 D、21

查看试题解析
3. 如图，在平面直角坐标系中，函数y＝2x和y＝﹣x的图象分别为直线l₁ ， l₂ ，过点（1，0）作x轴的垂线交l₁于点A₁ ，过点A₁作y轴的垂线交l₂于点A₂ ，过点A₂作x轴的垂线交l₁于点A₃ ，过点A₃作y轴的垂线交l₂于点A₄ ， …，依次进行下去，则点A₂₀₁₉的坐标为（）

A、（2¹⁰⁰⁹ ， 2¹⁰¹⁰） B、（﹣2¹⁰⁰⁹ ， 2¹⁰¹⁰） C、（2¹⁰⁰⁹ ， ﹣2¹⁰¹⁰） D、（﹣2¹⁰⁰⁹ ， ﹣2¹⁰¹⁰）

查看试题解析
4. 将抛物线 $y = x^{2} - 2 x - 1$ 向上平移1个单位，平移后所得抛物线的表达式是（）

A、 $y = x^{2} - 2 x$ B、 $y = x^{2} - 2 x - 2$ C、 $y = x^{2} - x - 1$ D、 $y = x^{2} - 3 x - 1$ .

查看试题解析
5. 如图，二次函数y＝ax²+bx+c的图象与x轴的一个交点坐标是（3，0），对称轴为直线x＝1，下列结论：①abc＞0；②2a+b＝0；③4a﹣2b+c＞0；④当y＞0时，﹣1＜x＜3；⑤b＜c.其中正确的个数是（　　）

A、2 B、3 C、4 D、5

查看试题解析
6. 如果1≤a≤ $\sqrt{2}$ ，则 $\sqrt{a^{2} - 2 a + 1}$ +|a-2|的值是（　　）

A、6+a B、﹣6﹣a C、﹣a D、1

查看试题解析
7. 如图，在△ABC和△ABD中，AB＝AC＝AD，AC⊥AD，AE⊥BC于点E，AE的反向延长线于BD交于点F，连接CD.则线段BF，DF，CD三者之间的关系为(　　)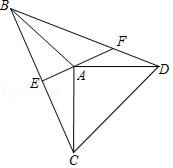

A、BF﹣DF＝CD B、BF+DF＝CD C、BF²+DF²＝CD² D、无法确定

查看试题解析
8. 已知A样本的数据如下：67，68，68，71，66，64，64，72，B样本的数据恰好是A样本数据每个都加6，则A、B两个样本的下列统计量对应相同的是（）

A、平均数 B、方差 C、中位数 D、众数

查看试题解析
9. 在下列等式中，不满足a≠0这个条件的是（　　）

A、a⁰＝1 B、 $a^{- 1} = \frac{1}{a}$ C、 $\sqrt{{(\frac{1}{a})}^{2}} = \frac{1}{a}$ D、 ${(\sqrt{a})}^{2} = a^{4}$

查看试题解析
10. 我国古代算书《九章算术》中第九章第六题是：今有池方一丈，葭生其中央，出水一尺，引葭赴岸，适与岸齐，问水深葭长各几何？你读懂题意了吗？请回答水深______尺，葭长_____尺.解：根据题意，设水深OB＝x尺，则葭长OA'＝（x+1）尺.可列方程正确的是（　　）

A、x²+5²＝（x+1）² B、x²+5²＝（x﹣1）² C、x²+（x+1）²＝10² D、x²+（x﹣1）²＝5²

查看试题解析
11. 在某校选拔毕业晚会主持人的决赛中，参与投票的每名学生必须从进入决赛的四名选手中选1名，且只能选1名，根据投票结果，绘制了如下两幅不完整的统计图，则选手B的得票为（）

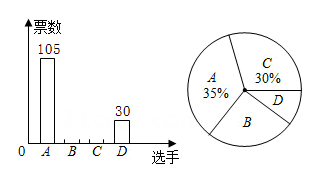A、300 B、90 C、75 D、85

查看试题解析
12. 如图，在正方形ABCD中，E是边BC上一点，且BE：CE＝1：3，DE交AC于点F，若DE＝10，则CF等于（）

A、 $\frac{24 \sqrt{2}}{7}$ B、 $3 \sqrt{3}$ C、 $\frac{32 \sqrt{2}}{7}$ D、 $6 \sqrt{2}$

查看试题解析

二、填空题

13. 已知x₁ ， x₂是方程x²﹣3x+1＝0的两个实数根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ ＝．

查看试题解析
14. 已知x﹣y=2，则x²﹣y²﹣4y=

查看试题解析
15. 抛物线 $y = a x^{2} - 2 a x + 5$ 的对称轴是直线.

查看试题解析
16. 已知 $\frac{17}{4}$ a²+10b²+ $\frac{1}{9}$ c²﹣4ab＝ $\frac{1}{3}$ a﹣2bc﹣ $\frac{1}{9}$ ，则a﹣2b+c＝.

查看试题解析
17. 计算：（﹣2）²⁰²³×0.5²⁰²²＝.

查看试题解析
18. 分解因式：m²+1﹣2m＝.

查看试题解析

三、解答题

19. 如图，在△ABC中，∠ACB＝90°，AC＝4，BC＝3，点D为边AB的中点.点P从点A出发，沿AC方向以每秒1个单位长度的速度向终点C运动，同时点Q从点C出发，以每秒2个单位长度的速度先沿CB方向运动到点B，再沿BA方向向终点A运动，以DP、DQ为邻边构造▱PEQD，设点P运动的时间为t秒.

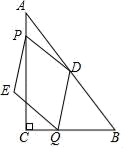(1)、设点Q到边AC的距离为h，直接用含t的代数式表示h；

(2)、当点E落在AC边上时，求t的值；

(3)、当点Q在边AB上时，设▱PEQD的面积为S（S＞0），求S与t之间的函数关系式；

(4)、连接CD，直接写出CD将▱PEQD分成的两部分图形面积相等时t的值.

查看试题解析
20. 如图，线段AB为的直径，点C、E在上，弧BC=弧CE，连接BE、CE，过点C作CM∥BE交AB的延长线于点M.

(1)、求证：直线CM是圆O的切线；

(2)、若sin∠ABE= $\frac{3}{5}$ ，BM=4，求圆O的半径.

查看试题解析
21. 如图，一次函数y＝mx+2与x轴、y轴分别交于点A（﹣1，0）和点B，与反比例函数y＝ $\frac{k}{x}$ 的图象在第一象限内交于点C（1，c）.

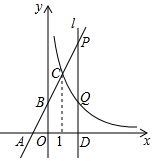(1)、求m的值和反比例函数的表达式；

(2)、过x轴上的点D（a，0）作平行于y轴的直线l（a>1），分别与直线AB和双曲线y＝ $\frac{k}{x}$ 交于点P、Q，且PQ＝2QD，求点D的坐标.

查看试题解析
22.
如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60°，又从A点测得D点的俯角β为30°，若旗杆底部G点为BC的中点，求矮建筑物的高CD．

查看试题解析
23. 某学校为了了解本校1200名学生的课外阅读的情况，现从各年级随机抽取了部分学生对他们一周的课外阅读时间进行了调查，并绘制出如下的统计图①和图②，根据相关信息，解答下列问题：

(1)、本次接受随机抽样调查的学生人数为图①中m的值为；

(2)、本次调查获取的样本数据的众数为，中位数为；

(3)、求本次调查获取的样本数据平均数；

(4)、根据样本数据，估计该校一周的课外阅读时间大于6h的学生人数.

查看试题解析
24. 某文化商店计划同时购进A、B两种仪器，若购进A种仪器2台和B种仪器3台，共需要资金1700元；若购进A种仪器3台，B种仪器1台，共需要资金1500元.

(1)、求A、B两种型号的仪器每台进价各是多少元？

(2)、已知A种仪器的售价为760元/台，B种仪器的售价为540元/台.该经销商决定在成本不超过30000元的前提下购进A、B两种仪器，若B种仪器是A种仪器的3倍还多10台，那么要使总利润不少于21600元，该经销商有哪几种进货方案？

查看试题解析
25. 已知：AB为⊙O的直径，点D、N在⊙O上，连接AD、BN交于点F，过点D作⊙O的切线交BA的延长线于点C，且CD⊥BE于点E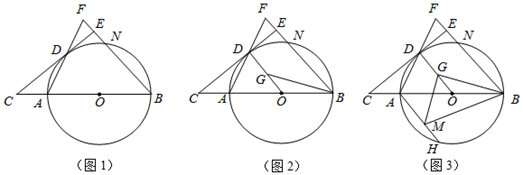

(1)、如图1，求证：AB＝BF；

(2)、如图2，连接OD，点G在OD上，连接BG，若BG＝CD，求证：∠ACD＝∠EBG；

(3)、如图3，在（2）的条件下，作AH//BE交⊙O于点H，过点G作MG⊥BG交AH于点M，连接MB，若DG＝8，MB＝25，求线段MG的长.

查看试题解析