湖北省恩施州鹤峰县2021年中考数学模拟试卷（一）

试卷更新日期：2022-03-25 类型：中考模拟

进入出卷网下载

一、单选题

1. 中华文明有着灿烂悠久的历史，对世界文明作出了巨大的贡献，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数，历史上首次使用了负数，如图，根据刘徽的这种表示方法，观察图①，可推算图②中所得的数值为（）

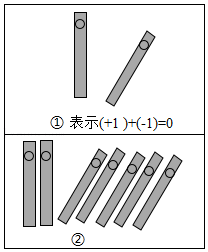A、7 B、5 C、 $- 3$ D、3

查看试题解析
2. 在2020年度“最美鹤峰”的县级评选中，某天，通过手机、电脑、平板等方式收看直播的观众达到了124000人，将124000人用科学记数法表示为（）

A、 $0.124 \times 10^{6}$ B、 $12.4 \times 10^{4}$ C、 $1.24 \times 10^{5}$ D、

查看试题解析
3. 下列运算中，正确的是（）

A、 $3 a + 5 a = 8 a$ B、 $a^{6} \div a^{3} = a^{2}$ C、 ${(3 a + 2 b)}^{2} = 9 a^{2} + 4 b^{2}$ D、 $\sqrt{20} \div \sqrt{5} = 4$

查看试题解析
4. 下列采用的调查方式中，合适的是（）

A、为了解东江湖的水质情况，采用抽样调查的方式 B、我市某企业为了解所生产的产品的合格率，采用普查的方式 C、某小型企业给在职员工做工作服前进行尺寸大小的调查，采用抽样调查的方式 D、某市教育部门为了解该市中小学生的视力情况，采用普查的方式

查看试题解析
5. 数学世界中充满了许多美妙的几何图形，等待着你去发现，如图是张老师用几何画板画出的四个图形，其中既是轴对称图形又是中心对称图形的是（）

A、①勾股树 B、②分形树 C、③谢尔宾斯三角形 D、④雪花

查看试题解析
6. 直线 $A B ∥ C D$ ，在 $A B$ 上任选一点E，将一直角三角板直角顶点放在E处， $∠ G = 30 °$ ，当 $∠ A E F = 70 °$ ，此时 $∠ C H F$ 的大小是（）

A、 $5 °$ B、 $10 °$ C、 $15 °$ D、 $20 °$

查看试题解析
7. 已知分式 $\frac{x^{2} - 3 x + 2}{x^{2} + 4 x - 5}$ 的值等于0，则x的取值是（）

A、 $x = 1$ B、 $x = 2$ C、 $x = 1$ 或 $x = 2$ D、 $x = - 5$

查看试题解析
8. 如图所示的几何体是由9个大小相同的小正方体组成的，将小正方体①移走后，所得几何体的三视图没有发生变化的是（）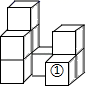

A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、主视图、左视图、俯视图

查看试题解析
9. 关于 $x$ 的不等式 $2 x + a \leq 1$ 只有2个正整数解，则 $a$ 的取值范围为（）

A、 $- 5 < a < - 3$ B、 $- 5 \leq a < - 3$ C、 $- 5 < a \leq - 3$ D、 $- 5 \leq a \leq - 3$

查看试题解析
10. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ C、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
11. 如图，在矩形 $A B C D$ 中， $A D = 5$ ， $A B = 10$ ，E、F为矩形外面的点， $B E = D F = 4$ ， $A F = C E = 3$ ，则EF=（）

A、 $\sqrt{221}$ B、15 C、20 D、 $9 \sqrt{3}$

查看试题解析
12. 如图是二次函数 $y = a x^{2} + b x + c$ 图象的一部分，抛物线与y轴交点位于 $(0 ， 2)$ 与 $(0 ， 3)$ 之间，给出四个结论：① $a b c < 0$ ，② $b > 1$ ，③ $4 a - 2 b + c < 0$ ，④ $a m^{2} + b m ⩾ a + b$ ，⑤当 $x = - 2.5$ 时， $y = y_{1}$ ，当 $x = 2.5$ 时， $y = y_{2}$ ，则 $y_{1} > y_{2}$ ，⑥关于x一元二次方程 $a x^{2} + b x + c - 5 = 0$ ，一定有两个不等的实根，其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. $\sqrt{16}$ 的平方根是．

查看试题解析
14. 已知 $m = 1 + \sqrt{2} ， n = 1 - \sqrt{2}$ ，则代数式 $\sqrt{m^{2} + n^{2} - 3 m n}$ 的值为.

查看试题解析
15. 已知正方形 $A B C D$ 边长为2， $D E$ 与以 $A B$ 的中点为圆心的圆相切交 $B C$ 于点E，求三角形 $D E C$ 的面积.

查看试题解析
16. 观察下列一组数的排列规律： $1 ， \frac{8}{5} ， \frac{15}{7} ， \frac{24}{9} ， \frac{35}{11} ， \frac{48}{13} ， \frac{63}{15} ， \frac{80}{17} ， \frac{99}{19} \dots$ 那么这一组数的第2021个数.

查看试题解析

三、解答题

17. 先化简，再求值：，其中m为方程 $m^{2} + m - 2 = 0$ 的一根.

查看试题解析
18. 如图，将▱ABCD的边DC延长到点E，使CE=DC，连接AE，交BC于点F．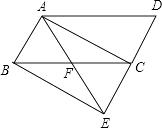

(1)、求证：△ABF≌△ECF；

(2)、若∠AFC=2∠D，连接AC、BE，求证：四边形ABEC是矩形．

查看试题解析
19. 为进一步做好青少年毒品预防工作，各级各类学校积极开展形式多样的“禁毒教育”，我县某中学对部分学生就禁毒知识的了解程度，采用随机抽查的方式，并根据收集到的信息进行统计，绘制了两幅尚不完整的统计图，根据图中信息回答下列问题：

(1)、接受问卷调查的学生共有人，条形统计图中m的值为；

(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为；

(3)、若该校共有学生800人，根据上述调查结果，可以估计出该校学生中对禁毒知识达到“非常了解”和“基本了解”程度的总人数为人；

(4)、若从禁毒知识达到“非常了解”程度的3名男生和3名女生中随机抽取2人去参加禁毒知识竞赛，请用列表或树状图的方法，求恰好抽到1名男生1名女生的概率.

查看试题解析
20. 在宜来高速建设过程中，途经如图某处山峰时，施工方案选择了沿直线 $A B$ 开凿穿山隧道，山顶有一铁塔，塔高35米，从与点C相距60米的点A测得E、F的仰角分别为， $38.53 °$ ，从与D点相距50米的点B测得F的仰角为 $45 °$ ，求隧道 $C D$ 的长度.（参考数据： $t a n 34.97 ° \approx 0.70$ ， $t a n 38.53 ° \approx 0.80)$

查看试题解析
21. 如图，在平面直角坐标系中，点A，D分别是x轴、y轴上的一动点，以 $A D$ 为边向外作矩形 $A B C D$ ，对角线BD∥x轴，反比例函数 $y = \frac{k}{x} (k > 0)$ 图象经过矩形对角线交点E.

(1)、如图1，若点A、D坐标分别是 $(6 ， 0)$ ， $(0 ， 2)$ ，求 $B D$ 的长；

(2)、如图2，保持点D坐标 $(0 ， 2)$ 不变，点A向右移移动，当点C刚好在反比函数图象上时，求点A坐标及k的值.

查看试题解析

22. 鹤峰县某茶叶加工企业，在助力精准扶贫行动中，推出惠农政策，连续用10天时间对清明前的毛尖鲜茶叶进行了收购，加工和销售.（当天收购的鲜茶叶，当天全部加工并销售完）经调查，整理出该茶叶经销商第x天

(0 < x ⩽ 10

，且x为整数）收购，加工和销售茶叶的相关信息如表：

鲜茶叶收购单价（元/ $kg$ ）	$200 - 10 x$
鲜茶叶收购量 $(kg)$
鲜茶叶加工后的成品茶重 $(kg)$	$33 - 3 x$
成品茶的销售单价（元/ $kg$ ）	900

(1)、若经销商连续两天共收购鲜茶叶

110 k g

，则这两天分别是第几天？

(2)、该茶叶经销商在第几天的毛利润最大，最大值是多少？（当天毛利润

=

成品茶销售金额

-

鲜茶叶收购金额）

(3)、当该公司在获得日最大毛利润后，将该天的全部毛利润作为第一次返还金返还给签约农户，用于生产发展资金，共返还三次，已知第三次返还给农户的金额为11664元，若每两次间返还金额的增长率a相同，求a的值.

查看试题解析

23. 如图， $A B$ 是 $⊙ O$ 的直径，点C、G为圆上的两点，当点C是弧 $B G$ 的中点时， $C D$ 垂直直线 $A G$ ，垂足为D，直线 $D C$ 与 $A B$ 的延长线相交于点P，弦 $C E$ 平分 $∠ A C B$ ，交 $A B$ 于点F，连接 $B E$ .

(1)、求证： $D C$ 与 $⊙ O$ 相切；

(2)、求证： $P C = P F$ ；

(3)、若 $\tan E = \frac{1}{3}$ ， $B E = \sqrt{5}$ ，求线段 $P F$ 的长.

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x + c$ 与x轴交于A，B两点，与y轴交于点C，已知 $O B = 2 O C = 4 O A$ .

(1)、若 $O A = 1$ ，求抛物线解析式及顶点坐标；

(2)、在（1）的条件下，抛物线对称轴是否存在一点Q，使得 $∠ A Q C = ∠ A B C$ ，若存在请求出Q点坐标，若不存在，请说明理由；

(3)、在（2）的条件下，若（2）中存在点Q，取x轴上方的点为点Q，若不存在，取点C关于x轴的对称点为点Q，点D为抛物线顶点，过点D作y轴垂线 $l_{1}$ ，点P为 $l_{1}$ 上任意一点，过点P作x轴垂线 $l_{2}$ ，点M为 $l_{2}$ 上一点，始终有 $P M = Q M$ ，设点P的横坐标为t，用含t的代数式表示点 $P M$ 的长， $P M$ 的最小值是多少.

查看试题解析