山东省淄博市临淄区2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-25 类型:期中考试
一、单选题
-
1. 下列说法中正确的是( )A、通过多次试验得到某事件发生的频率等于这一事件发生的概率 B、某人前 9 次掷出的硬币都是正面朝上,那么第 10 次掷出的硬币反面朝上的概率一定大于正面朝上的概率 C、不确定事件的概率可能等于 1 D、试验估计结果与理论概率不一定一致2. 下列用消元法解二元一次方程组中,不正确的是( )A、由①得: B、由①②得: C、由①②得: D、把①整体代入②得:3. 下列命题是真命题的是( )A、同旁内角互补 B、三角形的一个外角大于内角 C、三角形的一个外角等于它的两个内角之和 D、直角三角形的两锐角互余4. 在同一平面直角坐标系中,函数与的图象的交点坐标为( )A、 B、 C、 D、5. 若方程组 的解满足x+y=2020,则k等于( )A、2018 B、2019 C、2020 D、20216. 如果一个两位数的十位数字与个位数字之和为6,那么这样的两位数的个数是( )
A、3 B、6 C、5 D、47. 下列条件能判定直线l1∥l2的是( ) A、∠2=∠3 B、∠1=∠3 C、∠4+∠5=180° D、∠2=∠48. 有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面,则钥匙藏在黑色瓷砖下面的概率是( )
A、∠2=∠3 B、∠1=∠3 C、∠4+∠5=180° D、∠2=∠48. 有一把钥匙藏在如图所示的16块正方形瓷砖的某一块下面,则钥匙藏在黑色瓷砖下面的概率是( ) A、 B、 C、 D、9. 已知今年甲的年龄比乙的年龄多12岁,4年后甲的年龄恰好是乙的年龄的2倍,则甲今年的年龄是( )A、20岁 B、16岁 C、15岁 D、12岁10. 如图,将一张长方形纸条折叠,如果∠1=130°,则,∠2=( )
A、 B、 C、 D、9. 已知今年甲的年龄比乙的年龄多12岁,4年后甲的年龄恰好是乙的年龄的2倍,则甲今年的年龄是( )A、20岁 B、16岁 C、15岁 D、12岁10. 如图,将一张长方形纸条折叠,如果∠1=130°,则,∠2=( ) A、100° B、130° C、150° D、80°11. 如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是( )
A、100° B、130° C、150° D、80°11. 如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是( ) A、∠ABE=3∠D B、∠ABE+∠D=90° C、∠ABE+3∠D=180° D、∠ABE=2∠D
A、∠ABE=3∠D B、∠ABE+∠D=90° C、∠ABE+3∠D=180° D、∠ABE=2∠D二、多选题
-
12. 若将一副三角板按如图所示的方式放置,则下列结论正确的是( )
 A、∠1=∠2 B、如果∠2=30°,则有AC∥DE C、如果∠2=30°,则有BC∥AD D、如果∠2=30°,必有∠4=∠C
A、∠1=∠2 B、如果∠2=30°,则有AC∥DE C、如果∠2=30°,则有BC∥AD D、如果∠2=30°,必有∠4=∠C三、填空题
-
13. 将命题“对顶角相等”改为“如果…那么…”的形式为:.14. 某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是 .
 15. 若买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买4支圆珠笔、4本日记本需元.16. 已知直线 , 将一块含角的直角三角板按如图方式放置(),其中 , 两点分别落在直线 , 上,若 , 则的度数为 .
15. 若买2支圆珠笔、1本日记本需4元;买1支圆珠笔、2本日记本需5元,则买4支圆珠笔、4本日记本需元.16. 已知直线 , 将一块含角的直角三角板按如图方式放置(),其中 , 两点分别落在直线 , 上,若 , 则的度数为 .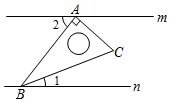 17. 已知方程组 的解是 . 则方程组 的解是 .
17. 已知方程组 的解是 . 则方程组 的解是 .四、解答题
-
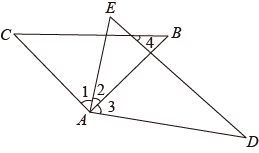
18. 小明准备完成题目:解方程组 , 发现系数“□”印刷不清楚.(1)、他把“□”猜成3,请你解此时的方程组 .(2)、张老师说:你在(1)中猜错了,我看到该题的正确答案里有结论: , 互为相反数.依此说法,问原题中的“□”是多少?19. 如图,的2倍与的和是 , 比大 , 且 , .
 (1)、求和的度数;(2)、求的度数.20. 一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜.(1)、当x=3时,谁获胜的可能性大?(2)、当x为何值时,游戏对双方是公平的?21. 在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
(1)、求和的度数;(2)、求的度数.20. 一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜.(1)、当x=3时,谁获胜的可能性大?(2)、当x为何值时,游戏对双方是公平的?21. 在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
(1)、按表格数据格式,表中的= ;= ;(2)、请估计:当次数s很大时,摸到白球的频率将会接近(精确到0.1);(3)、请推算:摸到红球的概率是(精确到0.1).22. 如图所示,与相交于点 , , 与互补. (1)、试说明;(2)、若 , , 求的度数.23. 阅读材料:
(1)、试说明;(2)、若 , , 求的度数.23. 阅读材料:小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
 (1)、请按照小明的思路完成上述问题:求每个小长方形的面积;(2)、某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是cm;(3)、小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.24. 如图所示,在△ABC中,点D、E、F分别是AB、AC、BC上的点,且∠ADE=90°,∠DEF=90°,点P是FC上一点,直线DP交直线EF于点G,试探究∠BDP与∠EGP之间的数量关系.
(1)、请按照小明的思路完成上述问题:求每个小长方形的面积;(2)、某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是cm;(3)、小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.24. 如图所示,在△ABC中,点D、E、F分别是AB、AC、BC上的点,且∠ADE=90°,∠DEF=90°,点P是FC上一点,直线DP交直线EF于点G,试探究∠BDP与∠EGP之间的数量关系. (1)、请你完成这道思考题;(2)、若将题中的条件“∠ADE=90°,∠DEF=90°,点P是FC上一点”改为“∠AED=∠C,∠B=∠DEF,点P是线段BC上一点(点P不与点F重合)”,其他条件均不变,则(1)中的结论是否仍然成立?请在备用图上画出图形,并说明理由.
(1)、请你完成这道思考题;(2)、若将题中的条件“∠ADE=90°,∠DEF=90°,点P是FC上一点”改为“∠AED=∠C,∠B=∠DEF,点P是线段BC上一点(点P不与点F重合)”,其他条件均不变,则(1)中的结论是否仍然成立?请在备用图上画出图形,并说明理由.
-