山东省威海市乳山市2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-25 类型：期中考试

进入出卷网下载

一、单选题

1. 下列成语所描述的事件为不可能事件的是（）

A、守株待兔 B、翁中捉鳖 C、百步穿杨 D、水中捞月

查看试题解析
2. 若 ${\begin{array}{l} x = 1 \\ y = - 2 \end{array}$ ，是关于 $x$ 和 $y$ 的二元一次方程 $m x + n y = 3$ 的解，则 $2 m - 4 n$ 的值等于 $($ $)$

A、3 B、6 C、 $- 1$ D、 $- 2$

查看试题解析
3. 下列四个命题中为真命题的是（）

A、两条直线被第三条直线所截，内错角相等 B、若 $∠ 1$ 和 $∠ 2$ 是对顶角，则 $∠ 1 = ∠ 2$ C、三角形的一个外角大于任何一个内角 D、 $a^{2} = b^{2}$ ，则 $a = b$

查看试题解析
4. 已知实数a，b满足：（a﹣b+3）²+ $\sqrt{a + b - 1}$ ＝0，则a²⁰²⁰+b⁶等于（）

A、65 B、64 C、63 D、62

查看试题解析
5. 不透明的袋子里有50张2022年北京冬奥会宣传卡片，每张卡片正面印有会徽吉祥物冰墩墩、吉祥物雪容融三种图案中的一种，卡片背面完全相同且不透明．印有冰墩墩的卡片共有n张，若从袋子里随机摸出1张卡片，印有冰图案的概率是 $\frac{1}{5}$ ，则n=（）

A、25 B、10 C、5 D、1

查看试题解析
6. 将长方形纸条如图进行折叠， $E F$ 是折痕， $∠ E F B = 32 °$ ，则 $∠ D F B$ =（）

A、148° B、138° C、126° D、116°

查看试题解析
7. 《九章算术》中记载：“今有共买羊，人出五，不足四十五：人出七，余三：问人数、羊价各几何？”其大意是：今有人合伙买羊，若每人出5钱，还差45钱；若每人出7钱，多余3钱，问合伙人数、羊价各是多少？设合伙人数为x人，羊价为y钱，根据题意，可列方程组为（）

A、 ${\begin{array}{l} y = 5 x + 45 \\ y = 7 x + 3 \end{array}$ B、 ${\begin{array}{l} y = 5 x + 45 \\ y = 7 x - 3 \end{array}$ C、 ${\begin{array}{l} y = 5 x + 45 \\ y = 7 x - 3 \end{array}$ D、 ${\begin{array}{l} y = 5 x - 45 \\ y = 7 x + 3 \end{array}$

查看试题解析
8. 如图，已知两个天平都处于平衡状态，那么四个小球的重量等同于小正方体的个数为（）

A、15个 B、14个 C、13个 D、12个

查看试题解析
9. 已知直线 $y = 3 x + 1$ 与直线 $y = m x + n$ 相交于点 $P (a ， 4)$ ，那么关于x的方程 $(m - 3) x + n = 1$ 的解为（）

A、 $x = 4$ B、 $x = - 4$ C、 $x = 1$ D、 $x = 2$

查看试题解析
10. 如图，将三角形纸片 $A B C$ 折叠， $D E$ 为折痕，点C落 $△ A B C$ 外的点F处， $∠ A = 65 °$ ， $∠ B = 75 °$ ， $∠ A E F = 35 °$ ，则 $∠ B D F =$ （）

A、95° B、105° C、115° D、125°

查看试题解析
11. 如图，下列条件能判断 $A D / / C B$ 的是（）

A、 $∠ D + ∠ D A B = 180 °$ B、 $∠ 1 = ∠ 2$ C、 $∠ 3 = ∠ 4$ D、 $∠ 4 = ∠ 5$

查看试题解析

二、多选题

12. 已知关于x，y的方程组 ${\begin{array}{l} x + y = 1 + 4 a \\ 2 x - y = - a - 7 \end{array}$
对于下列结论：
①当 $a = 0$ 时，方程组的解也是方程 $x + y = 1$ 的解；
②当 $x = y$ 时， $a = - \frac{5}{2}$
③a取任意实数， $3 x - y$ 的值始终不变；
④a取任意实数，都不能使 $2 x = 3 y$ 成立．
正确的是（）

A、① B、② C、③ D、④

查看试题解析

三、填空题

13. 如图，是一个可以自由转动的转盘，盘面被平均，分成6等份，分别标有数字2，3，4，5，6，7．转动转盘，当转盘停止时，指针指向区域所标示的数字即为转出的数字（若指针落在相邻两扇形交界处，重新转动转盘）．则转出的数字大于3的概率是．

查看试题解析
14. 将一副直角三角板如图所示放置，则 $∠ 1 =$ ．

查看试题解析
15. 若方程组 ${\begin{matrix} m + 4 n = 2 + 3 a \\ 5 m + 2 n = 1 - a \end{matrix}$ 的解满足 $m + n = 3$ ，则a=.

查看试题解析
16. 如图、利用两个正方形和两个长方形拼成一个大正方形，已知两个正方形的边长分别为 $3 c m$ 和 $4 c m$ ，将一个骰子任意抛向大正方形，落在黑色区域的概率是．

查看试题解析
17. 如图，用8块相同长方形地砖拼成一块宽为60厘米大的长方形地面，则大长方形的面积为．

查看试题解析

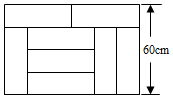
四、解答题

18. 在解方程组 ${\begin{array}{l} a x + 5 y = 15 \\ 4 x - b y = - 2 \end{array}$ 时，甲看错了方程组中a的值，得到的解为 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ ，乙看错了方程组中b的值，得到的解为 ${\begin{array}{l} x = 5 \\ y = 4 \end{array}$ ．求原方程组的解．

查看试题解析
19. 在一个不透明的口袋里装有4个白球和6个红球，它们除颜色外完全相同．

(1)、事件“从口袋里随机摸出一个球是绿球”发生的概率是；

(2)、事件“从口袋里随机摸出一个球是红球”发生的概率是；

(3)、从口袋里取走x个红球后，再放入x个白球，并充分摇匀，若随机摸出白球的概率是 $\frac{4}{5}$ ，求x的值．

查看试题解析
20. 学校开展校园艺术节系列活动，学生会代表小亮到文体超市购买文具奖品．小亮购买钢笔和签字笔共50支，其中钢笔标价每支8元，签字笔标价每支6元．经过沟通，老板对所购文具给予8折优惠，最终付费288元，小亮购买的钢笔和签字笔各多少支？

查看试题解析
21. 【信息阅读】
有些问题，所要求的结果往往不是某一个量的值，而是某些式子或问题的整体值.
如下面的问题：
问题：已知实数x，y同时满足3x- y =5①，和2x+3y =7②．求代数式7x+5y的值.
思路1：将①和②联立组成方程组，先求得x、y的值后，再代入7x +5y求值.
思路2：为降低运算量，由①+②×2，可直接得出7x+5y = 19．这样的解题思路即为整体思想.
【问题解决】

(1)、已知方程组 ${\begin{cases} 3 x + 2 y = 7 \\ 2 x + 3 y = 3 \end{cases}$ ，则x- y =；

(2)、若购买13支铅笔、5块橡皮、3本日记本共需33元；若购买25支铅笔、9块橡皮、3本日记本共需55元，求购买1支铅笔、1块橡皮、3本日记本共需多少元?

查看试题解析
22. 在数学活动课上，小明将一副三角尺的直角顶点O重合在一起，并对形成的角进行了系列化探究．

(1)、如图1，三角尺的斜边 $C D$ ， $A B$ 在同一直线上，则 $∠ A O C$ ．

(2)、如图2，将三角尺 $D O C$ 绕点O逆时针旋转， $A B$ 与 $O C$ 交于点E，若 $D C / / A O$ ，则 $∠ A E O$ ．

(3)、在图2的基础上，将三角尺 $D O C$ 继续绕点O逆时针旋转，使点B落在边 $D C$ 上， $A B$ 与 $O C$ 交于点E．利用图3补全图形，写出 $∠ A O E$ 与 $∠ A B C$ 间的等量关系，并证明你的结论．

查看试题解析
23. 已知： $C D$ 是经过 $∠ B C A$ 的顶点C的一条直线， $C A = C B$ ． E、F是直线 $C D$ 上两点， $∠ B E C = ∠ C F A = ∠ α$ ．

(1)、若直线 $C D$ 经过 $∠ B C A$ 的内部， $∠ B C D > ∠ A C D$ ．
①如图1， $∠ B C A = 90 °$ ， $∠ α = 90 °$ ，直接写出 $B E$ ， $E F$ ， $A F$ 间的等量关系： ▲ ．
②如图2， $∠ α$ 与 $∠ B C A$ 具有怎样的数量关系，能使①中的结论仍然成立？写出 $∠ α$ 与 $∠ B C A$ 的数量关系，并对结论进行证明；

(2)、如图3，若直线 $C D$ 经过 $∠ B C A$ 的外部， $∠ α = ∠ B C A$ ， ①中的结论是否成立？若成立，进行证明；若不成立，写出新结论并进行证明．

查看试题解析