山东省青岛市黄岛区2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-25 类型:期中考试
一、单选题
-
1. 计算﹣a2•a3的结果是( )A、a5 B、﹣a5 C、﹣a6 D、a62. 2021年春晚,大幅度融合了前沿科技手段.“”实现了高速率、低延迟的实时传输,为观众带来巨大的视听震撼,让人赞叹不已.一般情况下,网络的延迟时间只有秒,可以说是即时传输.将数据用科学记数法表示为( )A、 B、 C、 D、3. 如图,给出的下列条件中不能判断的是( )
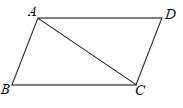 A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如果 , 那么所代表的代数式为( )A、 B、 C、 D、6. 小明一家自驾车到离家的某景点旅游,出发前将油箱加满油.下表记录了行驶路程与油箱余油量之间的部分数据:
A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如果 , 那么所代表的代数式为( )A、 B、 C、 D、6. 小明一家自驾车到离家的某景点旅游,出发前将油箱加满油.下表记录了行驶路程与油箱余油量之间的部分数据:行驶路程
…
油箱余油量
…
下列说法不正确的是( )
A、该车的油箱容量为 B、该车每行驶 耗油 C、油箱余油量与行驶路程之间的关系式为 D、当小明一家到达景点时,油箱中剩余油7. 2021年3月1日青岛市发改委公布了《关于青岛胶东国际机场机动车停放服务收费有关事项的通知(征求意见稿)》.《通知(征求意见稿)》规定(日以连续停放24小时计),可免费停放15分钟.在扣除免费时段后,连续停放时间2小时以内的(含2小时);停放时间超过2小时的部分,收费标准为每半小时2元,则单日停车费y(元)与停放时间t(小时)( )A、 B、
B、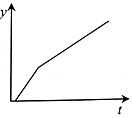 C、
C、 D、
D、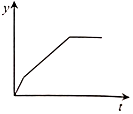 8. 如图,将长方形纸片ABCD,沿折痕MN折叠,B分别落在A1 , B1的位置,A1B1交AD于点E,若∠BNM=65°,以下结论:①∠B1NC=50°;②∠A1ME=50°;③A1M∥B1N;④∠DEB1=40°.正确的个数有( )
8. 如图,将长方形纸片ABCD,沿折痕MN折叠,B分别落在A1 , B1的位置,A1B1交AD于点E,若∠BNM=65°,以下结论:①∠B1NC=50°;②∠A1ME=50°;③A1M∥B1N;④∠DEB1=40°.正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 计算: .10. 如图,要使 , 可以添加的条件是(填写一个你认为正确的即可).
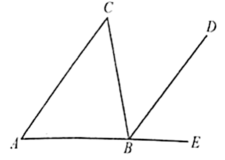 11. 如图,AB∥DE,AD⊥AB,AE平分∠BAC交BC于点F,如果∠CAD=24°,则∠E=°.
11. 如图,AB∥DE,AD⊥AB,AE平分∠BAC交BC于点F,如果∠CAD=24°,则∠E=°.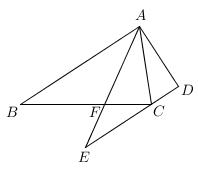 12. 已知 , , 则 .13. 若a3m=27,am﹣n=18,则an= .14. 有一个装有水的容器,如图所示,容器内的水面高度是15cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.3cm的速度匀速增加,则容器注满水之前,容器内的水面高度h(cm)与对应的注水时间t(秒)之间的关系式是 .
12. 已知 , , 则 .13. 若a3m=27,am﹣n=18,则an= .14. 有一个装有水的容器,如图所示,容器内的水面高度是15cm,现向容器内注水,并同时开始计时,在注水过程中,水面高度以每秒0.3cm的速度匀速增加,则容器注满水之前,容器内的水面高度h(cm)与对应的注水时间t(秒)之间的关系式是 .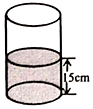 15. 如图,长方形ABCD的周长为24,以它的四条边为边长向外作正方形,如果这四个正方形的面积和为160,则长方形ABCD的面积为 .
15. 如图,长方形ABCD的周长为24,以它的四条边为边长向外作正方形,如果这四个正方形的面积和为160,则长方形ABCD的面积为 . 16. 如图1,在直角梯形ABCD中,AB∥CD,动点P从点B开始,沿B→C→D→A的方向以2cm/s的速度匀速运动(s),三角形ABP的面积为y(cm2),三角形ABP的面积y与运动时间x之间的变化关系如图2所示,根据图象信息,可得直角梯形ABCD的面积为 .
16. 如图1,在直角梯形ABCD中,AB∥CD,动点P从点B开始,沿B→C→D→A的方向以2cm/s的速度匀速运动(s),三角形ABP的面积为y(cm2),三角形ABP的面积y与运动时间x之间的变化关系如图2所示,根据图象信息,可得直角梯形ABCD的面积为 .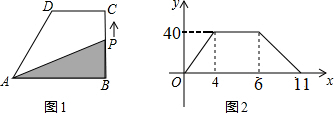
三、解答题
-
17. 作图题:已知:∠α、∠β、求作:∠AOB,使∠AOB=∠α+∠β
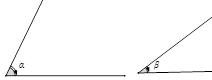 18. 计算(1)、;(2)、;(3)、;(4)、(用乘法公式计算).19. 先化简再求值
18. 计算(1)、;(2)、;(3)、;(4)、(用乘法公式计算).19. 先化简再求值, 其中 , .
20. 如图,已知∠1+∠2=180°,∠A=∠DCF,判断∠DCB和∠B之间有怎样的数量关系?请补充完整下面的说理过程:
解:∵∠1+∠2=180°
∴AD∥CF( ▲ )
∴∠A=∠CFB( ▲ )
∵∠A=∠DCF
∴∠CFB=∠DCF
∴ ▲ ∥ ▲ ( ▲ )
∴∠DCB+∠B=180°
 21. 若规定运算符号“▲”满足下列各式:
21. 若规定运算符号“▲”满足下列各式:▲
▲
▲
▲
▲
…
根据以上规律,求解下列各题:
(1)、▲;(2)、若 , 求▲的值.22. 如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线和线段分别表示甲、乙所行驶的路程和时间的关系,根据图回答下列问题: (1)、直接写出:甲出发1小时行驶了千米;乙的速度为千米/时;甲骑自行车在全程的平均速度为千米/时.(2)、请你根据图象上的数据,求出乙出发用多长时间就追上甲?23. 如图,AB∥CD,∠BAC的平分线AE交CD于点E.已知∠BAC=120°,∠ACN=20°,∠CNM=140°.
(1)、直接写出:甲出发1小时行驶了千米;乙的速度为千米/时;甲骑自行车在全程的平均速度为千米/时.(2)、请你根据图象上的数据,求出乙出发用多长时间就追上甲?23. 如图,AB∥CD,∠BAC的平分线AE交CD于点E.已知∠BAC=120°,∠ACN=20°,∠CNM=140°. (1)、判断MN与CD有怎样的位置关系,并说明理由.(2)、求∠AMN的度数.24. 已知 , 点为平面内的任意一点, .(1)、当点在如图①所示的位置时,与之间的数量关系是 .
(1)、判断MN与CD有怎样的位置关系,并说明理由.(2)、求∠AMN的度数.24. 已知 , 点为平面内的任意一点, .(1)、当点在如图①所示的位置时,与之间的数量关系是 . (2)、当点在如图②所示的位置时,与之间的数量关系是 .
(2)、当点在如图②所示的位置时,与之间的数量关系是 . (3)、当点在如图③所示的位置时,试判断与之间有怎样的数量关系,并说明理由.
(3)、当点在如图③所示的位置时,试判断与之间有怎样的数量关系,并说明理由. 25. 如图,在长方形ABCD中,AB=15厘米,BC=6厘米,点P从点A开始以3厘米/秒的速度沿AB边向点B运动;同时,点Q从点C开始以1厘米/秒的速度沿CB边向点B运动,点P到达点B时,P,Q两点同时停止运动.设运动时间为t秒.解答下列问题:
25. 如图,在长方形ABCD中,AB=15厘米,BC=6厘米,点P从点A开始以3厘米/秒的速度沿AB边向点B运动;同时,点Q从点C开始以1厘米/秒的速度沿CB边向点B运动,点P到达点B时,P,Q两点同时停止运动.设运动时间为t秒.解答下列问题: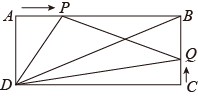 (1)、当t为何值时,线段BQ的长度等于线段BP的长度?(2)、连接BD,当t为何值时,三角形BDQ的面积等于长方形ABCD的面积的?(3)、设三角形DPQ的面积为y2(厘米2),求y2与t的关系式.
(1)、当t为何值时,线段BQ的长度等于线段BP的长度?(2)、连接BD,当t为何值时,三角形BDQ的面积等于长方形ABCD的面积的?(3)、设三角形DPQ的面积为y2(厘米2),求y2与t的关系式.