山东省青岛市城阳区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-25 类型：期中考试

进入出卷网下载

一、单选题

1. 计算（－3xy³）³ ，结果正确的是（）．

A、－9x³y⁵ B、－27x³y⁶ C、－27x³y⁹ D、－9x³y⁹

查看试题解析
2. 如图，直线a，b分别与c相交，在标出的角∠2，∠3，∠4，∠5中，与∠1是内错角的是（）

A、∠2 B、∠3 C、∠4 D、∠5

查看试题解析
3. 已知一个三角形两边的长分别是5和8，则此三角形第三边的长不可能是（）

A、3 B、5 C、7 D、10

查看试题解析
4. 若长方形面积是3a²－3ab＋9a，一边长为3a，则这个长方形的周长是（）

A、8a－2b＋6 B、2a－2b＋6 C、8a－2b D、a－b＋3

查看试题解析
5. 下列结论正确的有（）
①两条直线相交，所得的四个角中有一个角是90°，这两条直线一定互相垂直
②三角形的三条角平分线交于一点，这点称为三角形的重心
③直线AB⊥CD，也可以说成直线CD⊥AB
④直线外一点与直线上各点连接的所有线段中，垂线段最短

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 定义a $\otimes$ b＝（a－2）（b＋1），例如2 $\otimes$ ³＝（2－2）×（3＋1）＝0×4＝0，则（x＋1） $\otimes$ x的结果为（）

A、x－1 B、x²＋2x＋1 C、．x²－2 D、x²－1

查看试题解析
7. 如图，直线a∥b，直线l与a，b分别相交于A，B两点，过点A作直线l的垂线交直线b与点C，若∠2＝27°，则∠1的度数为（）

A、53° B、63° C、73° D、27°

查看试题解析
8. 为响应我区“绿色出行，万步有约”活动，小亮步行上下学，学校到小亮家的总路程为1700米．一天放学后，小亮以35米/分的速度回家，走到离学校700米时，小亮在书店看了40分钟书，之后以100米/分的速度步行回家．以下是他放学后从学校到家所用时间t（分）与离家距离s（米）的关系图象．下列结论：①a＝20分；②c＝60分；③b＝1000米；④自变量是小亮放学后从学校到家所用时间t（分），因变量是小亮离家的距离s（米），正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 如果一个角的补角是142°，那么这个角的余角是．

查看试题解析
10. 在△ABC中，若∠A：∠B：∠C＝2：3：5，则此三角形是三角形．

查看试题解析
11. 某病毒今日呈爆发高峰期，其病毒颗粒呈多样性，期中球型病毒的最大直径为0.0000000072m，则这个数字0.0000000072用科学记数法表示为．

查看试题解析
12. 已知a^m＝3，aⁿ＝2，则a^3m﹣²ⁿ＝．

查看试题解析
13. 某超市进了一批草莓，出售时销售量x与销售总价y的关系如下表：
销售量x（kg）
1
2
3
4
5
…
销售总价y（元）
12＋0.5
24＋1
36＋1.5
48＋2.0
60＋2.5
…
请根据上表中的数据写出销售总价y（元）与销售量x（kg）之间的关系式：

查看试题解析
14. 如图，CB平分∠DBE，∠3＝∠4，若∠1＝48°，∠2＝132°，则∠ADB＝°

查看试题解析
15. 如图，若AD是△ABC的BC边上的高，AE是∠BAC的角平分线，∠C＝42°，∠BAE＝15°，则∠DAB＝°

查看试题解析
16. 数学兴趣小组发现：
（x－1）（x＋1）＝x²－1
（x－1）（x²＋x＋1）＝x³－1
（x－1）（x³＋x²＋x＋1）＝x⁴－1
利用你发现的规律：求： $7^{2021} + 7^{2020} + 7^{2019} + \dots + 7 + 1$ ＝

查看试题解析

三、解答题

17. 用圆规、直尺作图，不写做法，但要保留作图痕迹．
已知：如图，△ABC
求作：直线MN，使MN∥AC，且MN经过点B

查看试题解析
18.

(1)、 ${(- a)}^{5} \cdot a^{3} + {(- 3 a^{4})}^{2}$

(2)、 ${(- 1)}^{2020} + {(- 2)}^{3} +$ （π－1）⁰ $+ {(- \frac{1}{4})}^{- 2}$

(3)、 $(3 a^{3} b - a b^{2} + \frac{1}{3} a b) \div (- \frac{1}{3} a b)$

(4)、 $(16 a b^{3} - 8 a^{3} b) \div 4 a b + (a + 2 b) (a - 2 b)$

查看试题解析
19. 先化简，再求值：

(1)、 ${(3 a - b)}^{2} + (a + 2 - b) (a + 2 + b) - {(a + 2)}^{2}$ ，其中 $a = \frac{1}{3}$ ， b＝－3

(2)、 $(m^{2} n - 2 m n^{2} - n^{3}) \div n - (m + n) (m - n)$ ，其中m＝ $- \frac{1}{25}$ ， n＝－50

查看试题解析
20. 已知AB⊥BC，AB⊥DE，垂足分别为B，D，∠1＝∠2，求证：∠BEC＋∠FGE＝180°
请你将证明过程补充完整．
证明：∵AB⊥BC，AB⊥DE，垂足分别为B，D（已知）
∴∠ABC＝∠ADE＝90°（垂直定义）
∴                  ▲                  （                  ▲                  ）
∴∠1＝                  ▲                  （                  ▲                  ）
又∵∠l＝∠2（已知）
∴∠2＝                  ▲
∴                  ▲                  （                  ▲                  ）
∴∠BEC＋∠FGE＝180°（                  ▲                  ）

查看试题解析
21. 如图所示，梯形ABCD上底的长是xcm，下底长BC＝25cm，高DE＝10cm．

(1)、梯形面积y（cm²）与上底长xcm之间的关系式是什么？

(2)、用表格表示当x从1cm变到6cm时（每次增加1cm），y（cm²）的相应值；
xcm
1
2
3
4
5
6
y（cm²）

(3)、当x每增加1cm时，y如何变化？说说你的理由．

(4)、当x＝0时，y等于什么？此时y表示的是什么？

查看试题解析
22. 已知：∠DAC＋∠ACB＝180°，∠1＝∠2，∠3＝∠4，∠ACF＝24°，∠DAC＝4∠5，求证：

(1)、CE平分∠BCF

(2)、则∠5＝°（直接写出答案即可）

查看试题解析
23. 2020年武汉发生新冠肺炎疫情，“一方有难，八方支援”，我市迅速组织一百多名医护工作者并捐赠一批医疗物资从青岛出发前往武汉支援抗疫，大巴与货车走不同路线，大巴路线比货车路线多200km，货车在大巴出发1小时后出发，货车的平均速度是100千米/小时，途中没有休息安全到达武汉．设大巴出发x小时候行走的路程为y千米．图中的折线表示大巴在整个行走过程中y随x的变化关系

(1)、大巴行走的总路线是千米，途中休息了小时

(2)、大巴在休息前所走的路段上速度为千米/时；

(3)、大巴在休息后所走的路段上速度为千米/时；

(4)、当货车到武汉时，大巴离终点武汉的路程是多少？（写出解答过程）

查看试题解析
24. 【发现问题】数形结合是解决数学问题的一种重要的思想方法，借助图的直观性，可以帮助我们更容易理解数学问题．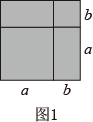
例如，求图1阴影部分的面积，可以得到乘法公式（a＋b）²＝a²＋2ab＋b²
请解答下列问题：

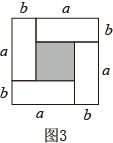
(1)、请写出求图2阴影部分的面积能解释的乘法公式（直接写出乘法公式即可）

(2)、用4个全等的、长和宽分别为a、b的长方形，拼摆成如图3的正方形，请你观察求图3中阴影部分的面积，蕴含的相等关系，写出三个代数式：（a＋b）²、（a－b）²、ab之间的等量关系式（直接写出等量关系式即可）

(3)、【自主探索】
小明用图4中x张边长为a的正方形，y张边长为b的正方形，z张宽为a，长为b的长方形纸片拼出一个面积为（3a＋2b）（2a＋3b）长方形，请在下面方框中画出图形，并计算x＋z＝

(4)、【拓展迁移】
事实上，通过计算几何图形的体积也可以表示一些代数恒等式，图5表示的是一个边长为a＋b的正方体，请你根据图5求正方体的体积，写出一个代数恒等式：

查看试题解析

销售量x（kg）	1	2	3	4	5	…
销售总价y（元）	12＋0.5	24＋1	36＋1.5	48＋2.0	60＋2.5	…

xcm	1	2	3	4	5	6
y（cm²）