山东省济宁市梁山县2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-25 类型：期中考试

进入出卷网下载

一、单选题

1. 0的算术平方根是（）

A、 $- 1$ B、 $1$ C、 $± 1$ D、 $0$

查看试题解析
2. 若a、b、c是同一平面内三条不重合的直线，则它们的交点可以有（　　）

A、1个或2个或3个 B、0个或1个或2个或3个 C、1个或2个 D、以上都不对

查看试题解析
3. 如图是雷达探测到的6个目标，若目标C用（40，120°）表示，目标D用（50，210°）表示，则（30，240°）表示的目标是（）

A、目标A B、目标B C、目标F D、目标E

查看试题解析
4. 在下列方程中，是二元一次方程的（）

A、 $3 x + \frac{1}{3} = 8$ B、 $3 x + \frac{3}{y} = 1$ C、 $\frac{x - 2}{3} + 2 y = 4$ D、 $x^{2} = 5 y + 1$

查看试题解析
5. 如图，直线a∥b，则直线a，b之间距离是（）

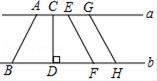A、线段AB的长度 B、线段CD的长度 C、线段EF的长度 D、线段GH的长度

查看试题解析
6. 一个正数的两个不同的平方根是 a +4 和 2 a−1，则这个正数是（）

A、1 B、4 C、9 D、16

查看试题解析
7. 已知 $M (2 + x ， 9 - x^{2})$ 在x轴的负半轴上，则点M的坐标为（）

A、 $(- 1 ， 0)$ B、 $(- 3 ， 0)$ C、 $(0 ， - 3)$ D、 $(1 ， 1)$

查看试题解析
8. 已知非负整数x、y满足方程 $3 x + 2 y = 7$ ．则方程 $3 x + 2 y = 7$ 的解是（）

A、 $x = 1$ 或 $y = 2$ B、 $x = 1$ 且 $y = 2$ C、 $x = 3$ 或 $y = - 1$ D、 $x = 3$ 且 $y = - 1$

查看试题解析
9. 若 $a / / b$ ，则下列图中能直接利用“两直线平行，内错角相等”判定 $∠ 1 = ∠ 2$ 的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，直线AB与直线CD相交于点O，OE⊥AB，垂足为O，∠EOD＝ $\frac{1}{2}$ ∠AOC，则∠BOC等于（）

A、120° B、130° C、150° D、160°

查看试题解析
11. 方程组 ${\begin{matrix} | 2 x | + y = 8 \\ 2 x + | y | = 4 \end{matrix}$ 的解的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
12. 观察图中每一个正方形各顶点所标数字的规律，2021应标在（）

A、第505个正方形右下角顶点处 B、第504个正方形右上角顶点处 C、第506个正方形右下角顶点处 D、第506个正方形左上角顶点处

查看试题解析

二、填空题

13. 已知点 $P (a ， b)$ 在坐标轴上，则 $a b =$ ．

查看试题解析
14. 直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上的一点由原点到达O′点，点O′对应的数是．

查看试题解析
15. 下列命题：①相等的角是对顶角；②平面内，过一点有且只有一条直线与已知直线垂直；③平行于同一条直线的两条直线互相平行；④同角或等角的余角相等，其中假命题是（填序号）．

查看试题解析
16. 某班进行个人投篮比赛，受污损的下表记录了在规定时间内投进几个球的人数分布情况，已知进球3个或3个以上的人平均每人投进3.5个球，进球4个或4个以下的人平均每人投进2.5个球，则投进3个球的、投进4个球的依次有人．
进球数n（个）
0
1
2
3
4
5
投进n个球的人数
1
2
7
2

查看试题解析
17. 如图，直线 $l_{1} / / l_{2} ， ∠ α = ∠ β ， ∠ 1 = 50^{°}$ ， $∠ 2 =$ ．

查看试题解析
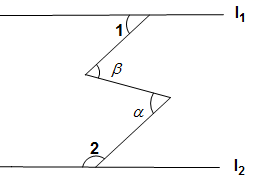18. 解方程组 ${\begin{array}{l} a x + b y = 2 \\ c x - 7 y = 8 \end{array}$ 时，一学生把c看错得 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ ，已知方程组的符合题意解是 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ ，则abc值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{49} - \sqrt[3]{64}$ ．

(2)、 $(\sqrt{3})^{2} + | 1 - \sqrt{3} | - (\sqrt{3} + 1)$ ．

查看试题解析
20. 解方程组

(1)、 ${\begin{matrix} 3 x + 2 y = 1 \\ x - 2 y = 3 \end{matrix}$

(2)、 ${\begin{matrix} y - 1 = 3 （ x - 2 ） \\ \frac{x}{4} + \frac{y}{3} = \frac{4}{3} \end{matrix}$

查看试题解析
21. 完成下列推理，并填空：
已知，如图，∠BAE+∠AED＝180°，∠M＝∠N，试说明：∠1＝∠2．
解：∵∠BAE+∠AED＝180（已知），
∴AB∥CD（                  ▲                  ）．
∴∠BAE＝                  ▲                  （两直线平行，内错角相等）．
又∵∠M＝∠N（已知），
∴AN∥EM（                  ▲                  ）．
∴∠NAE＝∠MEA（                  ▲                  ）．
∴∠BAE﹣∠NAE＝                  ▲                  ﹣                  ▲                  （等式性质）．
即∠1＝∠2．

查看试题解析
22.

(1)、在如图所示的平面直角坐标系中表示下面各点：
A（0，3）；B（5，0）；C（3，﹣5）；D（﹣3，﹣5）；E（3，5）；

(2)、A点到原点的距离是；

(3)、将点C向x轴的负方向平移6个单位，它与点重合；

(4)、连接CE，则直线CE与y轴是什么位置关系；

(5)、点D分别到x、y轴的距离是多少．

查看试题解析
23. 将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F，

(1)、求证：CF∥AB，

(2)、求∠DFC的度数.

查看试题解析
24. 先阅读材料，再求解．
若x是不等于1的实数，我们把 $\frac{1}{1 - x}$ 称为x的差倒数，如2的差倒数是 $\frac{1}{1 - x} = -$ 1，﹣1的差倒数为 $\frac{1}{1 - (- 1)} = \frac{1}{2}$ ，现已知x₁＝ $\frac{1}{3}$ ， x₂是x₁的差倒数，x₃是x₂的差倒数，x₄是x₃的差倒数，…，依此类推……；

(1)、x₂＝， x₃＝， x₄＝；

(2)、求x₁₀₀的值；

(3)、求x₂₀₂₁的值．

查看试题解析
25. 济宁市某校准备组织教师、学生、学生家长到某地进行参观学习活动，旅行社代办购买动车票，动车票价格如下表所示：
运行区间
大人票价
学生票
出发站
终点站
一等座
二等座
二等座
曲阜
某地
65（元）
54（元）
40（元）
根据报名总人数，若所有人员都买一等座的动车票，则共需13650元，若都买二等座动车票（学生全部按表中的“学生票二等座”购买），则共需8820元；已知学生家长的人数是教师的人数的2倍．

(1)、设参加活动的老师有m人，请直接用含m的代数式表示教师和学生家长购买动车票所需的总费用；

(2)、求参加活动的总人数．

查看试题解析
26. 学习数学应该积极地参加到现实的、探索性的数学活动中去，努力地成为学习的主人．如图，请你探究：随着D点位置的变化，∠BDC与∠A的大小关系．要求：（1）、（2）、（3）问用“＞或＜”表示其关系，（4）、（5）问用“＝”表示其关系；（1）、（2）、（3）直接写出结论，（4）、（5）写出推理过程．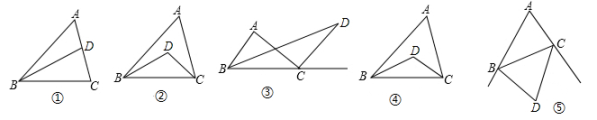

(1)、如图①，点D在AC上（不同于A，C两点），∠BDC与∠A的关系是；

(2)、如图②，点D在△ABC内部，∠BDC与∠A的关系是；

(3)、如图③，点D在△ABC外部，∠BDC与∠A的关系是；

(4)、如图④，点D是∠ABC，∠ACB平分线的交点，此时∠BDC＝90°+ $\frac{1}{2}$ ∠A；写出该结论的推理过程；

(5)、如图⑤，点D是∠ABC与∠ACB的两外角∠CBE与∠CBE的角平分线的交点，∠BDC与∠A的关系又如何？试说明理由．

查看试题解析

运行区间		大人票价		学生票
出发站	终点站	一等座	二等座	二等座
曲阜	某地	65（元）	54（元）	40（元）

进球数n（个）	0	1	2	3	4	5
投进n个球的人数	1	2	7			2