山东省济南市历下区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-25 类型：期中考试

进入出卷网下载

一、单选题

1. 下面是青岛、济南、郑州、太原四个城市的地铁图标，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，要把河中的水引到村庄A，小凡先作AB⊥CD，垂足为点B，然后沿AB开挖水渠，就能使所开挖的水渠最短，其依据是（）

A、两点确定一条直线 B、两点之间线段最短 C、直线外一点与直线上各点连接的所有线段中，垂线段最短 D、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线

查看试题解析
3. 下列运算正确的是（）

A、a²•a³＝a⁶ B、（a²）³＝a⁵ C、（2a²）³＝6a⁶ D、a³÷a²＝a（a≠0）

查看试题解析
4. 如图，在 $△ A B C$ 中， $∠ B A C = 40 °$ ， $∠ B = 60 °$ ， $A D // B C$ ，则 $∠ D A C$ 大小为（）

A、 $20 °$ B、 $40 °$ C、 $60 °$ D、 $80 °$

查看试题解析
5. 下列说法正确的是（）

A、两个等边三角形一定是全等图形 B、两个全等图形面积一定相等 C、形状相同的两个图形一定全等 D、两个正方形一定是全等图形

查看试题解析
6. 石墨烯是目前世界上最薄却又最坚硬同时还是导电性能最好的纳米材料，其理论厚度大约仅0.00 000 034纳米．将0.00 000 034用科学记数法表示为（　　）

A、 $3.4 \times 10^{- 7}$ B、 $3.4 \times 10^{- 8}$ C、 $34 \times 10^{- 8}$ D、 $0.34 \times 10^{- 6}$

查看试题解析
7. 若一个三角形的两边长分别为3 $cm$ 、6 $cm$ ，则它的第三边的长可能是（）

A、2 $cm$ B、3 $cm$ C、6 $cm$ D、9 $cm$

查看试题解析
8. 如图，用直尺和圆规作一个角等于已知角，能得出∠A′O′B′＝∠AOB的依据是（）

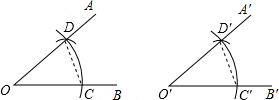A、SSS B、SAS C、ASA D、AAS

查看试题解析
9. 如图，点B，C在线段AD上，AB＝CD，AE∥BF，添加一个条件仍不能判定△AEC≌△BFD的是（）

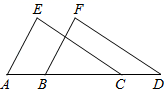A、AE＝BF B、CE＝DF C、∠ACE＝∠BDF D、∠E＝∠F

查看试题解析
10. 在下列条件：①∠A+∠B＝∠C，②∠A：∠B：∠C＝5：3：2，③∠A＝90°﹣∠B，④∠A＝2∠B＝3∠C中，能确定△ABC是直角三角形的条件有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 小华和小明是同班同学，也是邻居，某日早晨，小明7：40先出发去学校，走了一段后，在途中停下吃了早餐，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公共汽车到了学校，如图是他们从家到学校已走的路程 $S$ （米）和所用时间 $t$ （分钟）的关系图，则下列说法中不正确的是（）

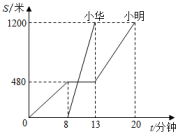A、小明家和学校距离1200米 B、小华乘公共汽车的速度是240米/分 C、小华乘坐公共汽车后7：50与小明相遇 D、小明从家到学校的平均速度为80米/分

查看试题解析
12. 如图，直线AB∥CD，EF分别交AB、CD于E、F两点，作∠BEF、∠DFE的平分线相交于点K；作∠BEK、∠DFK的平分线相交于点K₁；依此类推，作∠BEK₁、∠DFK₂的平分线相交于点K₂ ， …，作∠BEKn_﹣₁、∠DFKn_﹣₁的平分线相交于点Kn，则∠Kn的与∠K的关系为（）

A、∠Kn＝ $\frac{1}{2^{n}}$ ∠K B、∠Kn＝ $\frac{1}{2^{n}}$ ∠K C、∠Kn＝ $\frac{1}{2^{n + 1}}$ ∠K D、∠Kn＝ $\frac{1}{2 (n + 1)}$ ∠K

查看试题解析

二、填空题

13. 利用完全平方公式计算：（m+3）²＝．

查看试题解析
14. 如图，有一座小山，现要在小山A ， B的两端开一条隧道，施工队要知道A ， B两端的距离，于是先在平地上取一个可以直接到达点A和点B的点C ，连接AC并延长到D ，使CD＝CA ，连接BC并延长到E ，使CE＝CB ，连接DE ．经测量DE ， EC ， DC的长度分别为800 m，500 m，400 m，则A ， B之间的距离为m．

查看试题解析
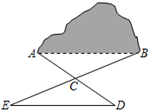15. 如图，一般轮船按箭头所示方向行驶，C处有一灯塔，当轮船从A点行驶到B点时，∠ACB＝°．

查看试题解析
16. 如图，在△ABC中，∠BAC＝130°，∠C＝40°，AD、AE分别是它的高线和角平分线，则∠DAE的度数是°．

查看试题解析
17. 任意给一个非零数，按下列程序进行计算，则输出结果为．

查看试题解析
18. 如图，将△ABC沿直线AC翻折得到△ADC，连接BD交AC于点E，AF为△ACD的中线，若BE＝2，AE＝3，△AFC的面积为2，则CE= ．

查看试题解析

三、解答题

19. 计算：

(1)、（﹣2）²﹣（ $\frac{1}{2}$ ）^﹣¹+（π﹣5）⁰；

(2)、（3x²﹣xy²+ $\frac{1}{2}$ xy）÷（﹣ $\frac{1}{2}$ xy）．

查看试题解析
20. 一个角的余角的3倍与它的补角相等，求这个角的度数．

查看试题解析
21. 如图，在正方形网格中，△ABC是格点三角形．

(1)、画出△A₁B₁C₁ ，使得△A₁B₁C₁和△ABC关于直线l对称；

(2)、过点C作线段CD，使得CD∥AB，且CD＝AB；

(3)、求以A、B、C、D为顶点的四边形的面积．

查看试题解析
22. 如图所示，点B、E分别在AC、DF上，BD、CE均与AF相交，∠1＝∠2，∠C＝∠D．
求证：

(1)、BD∥CE；

(2)、∠A＝∠F．

查看试题解析
23. 如图，已知C是线段AE上的一点，DC⊥AE，DC＝AC，B是CD上一点，且CB＝CE．

(1)、求证：△ABC≌△DEC；

(2)、若∠A＝20°，求∠E的度数．

查看试题解析
24. 如图1的两个长方形可以按不同的形式拼成图2和图3两个图形．

(1)、在图2中的阴影部分的面积S₁可表示为；（写成多项式乘法的形式）；在图3中的阴影部分的面积S₂可表示为；（写成两数平方差的形式）；

(2)、比较图2与图3的阴影部分面积，可以得到的等式是____ ；

A、（a+b）²＝a²+2ab+b² B、（a+b）（a﹣b）＝a²﹣b² C、（a﹣b）²＝a²﹣2ab+b²

(3)、请利用所得等式解决下面的问题：
①已知4m²﹣n²＝12，2m+n＝4，则2m﹣n＝ ▲ ；
②计算（2+1）（2²+1）（2⁴+1）（2⁸+1）+…+（2³²+1）+1的值，并直接写出该值的个位数字是多少．

查看试题解析
25. 如图，某品牌自行车每节链条的长度为2.5cm，交叉重叠部分的圆的直径为0.8cm．

(1)、观察图形，填写下表：
链条节数/x（节）
2
3
4
…
链条长度/y（cm）
4.2
…

(2)、上表的两个变量中，自变量是；因变量是；

(3)、请你写出y与x之间的关系式；

(4)、如果一辆自行车的链条（安装前）共由60节链条组成，那么链条的总长度是多少？

查看试题解析
26. 如图1，∠EFH＝90°，点A、C分别在射线FE和FH上，AB∥CD．

(1)、若∠FAB＝150°，则∠HCD＝°；

(2)、小明同学发现：无论∠FAB如何变化，∠FAB﹣∠HCD的值始终为定值，并给出了一种证明该发现的辅助线作法：如图2，过A作AM∥FH，交CD于M，请你根据小明同学提供的辅助线（或自己添加其它辅助线），先确定该定值，并说明理由；

(3)、如图3，把“∠EFH＝90°”改为“∠EFH＝120°”，其它条件保持不变，猜想∠FAB与∠HCD的数量关系，并说明理由．

查看试题解析
27.

(1)、方法学习：数学兴趣小组活动时，张老师提出了如下问题：如图1，在△ABC中，AB＝8，AC＝6，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法（如图2），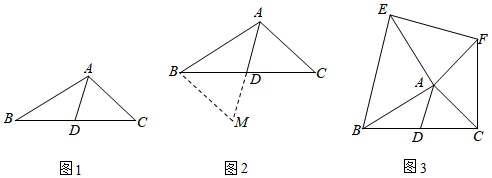
①延长AD到M，使得DM＝AD；
②连接BM，通过三角形全等把AB、AC、2AD转化在△ABM中；
③利用三角形的三边关系可得AM的取值范围为AB﹣BM＜AM＜AB+BM，从而得到AD的取值范围是多少；

(2)、请你写出图2中AC与BM的数量关系和位置关系，并加以证明．

(3)、深入思考：如图3，AD是△ABC的中线，AB＝AE，AC＝AF，∠BAE＝∠CAF＝90°，请直接利用（2）的结论，试判断线段AD与EF的数量关系，并加以证明．

查看试题解析

链条节数/x（节）	2	3	4	…
链条长度/y（cm）	4.2			…