山东省德州市乐陵市2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-25 类型：期中考试

进入出卷网下载

一、单选题

1. 如图， $∠ 1$ 与 $∠ 2$ 是（）

A、同位角 B、内错角 C、同旁内角 D、对顶角

查看试题解析
2. 在平面直角坐标系中，点 $A (- 4, 5)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列生活中的实例，可以用“两点之间线段最短”来解释的是（）

A、小狗看到远处的食物，总是径直奔向食物 B、从一条河道能向集镇引一条最短的水渠 C、把一根木条固定到墙上需要两颗钉子 D、经过刨平木板上的两个点，能弹出一条笔直的墨线

查看试题解析
4. 初中第一学年的学习生活就要结束了，在你们成长的花季里，一定有很多收获。很高兴和你们合作完成第一道考试题。现在我作一个 $120 °$ 的角，你作一个 $60 °$ 的角，下面结论正确的是（）

A、这两个角是邻补角 B、这两个角是同位角 C、这两个角互为补角 D、这两个角是同旁内角

查看试题解析
5. 下列数据能确定物体具体位置的是（）

A、明华小区东 B、希望路右边 C、东经118°，北纬28° D、北偏东30°

查看试题解析
6. 下列方程中是二元一次方程组的是（）

A、 ${\begin{matrix} x + y = 4 \\ \frac{1}{x} + \frac{1}{y} = 9 \end{matrix}$ B、 ${\begin{matrix} x + y = 5 \\ y + z = 7 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ 3 x - 2 y = 6 \end{matrix}$ D、 ${\begin{matrix} x - y = x y \\ x + y = 1 \end{matrix}$

查看试题解析
7. 下列句子中，属于命题的是（）
①三角形的内角和等于180度；②对顶角相等；③过一点作已知直线的垂线；④两点确定一条直线.

A、①④ B、①②④ C、①②③ D、②③

查看试题解析
8. 如图是某节数学课上王老师和琪琪的对话，根据对话内容，判定 $A E / / C D$ 的依据是（）

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、内错角互补，两直线平行 D、同旁内角互补，两直线平行

查看试题解析
9. 下列各数中，无理数有（）
$3.1415 ， \frac{12}{7}$ ， 0.321，π，2.32232223…（相邻两个3之间的2的个数逐次增加1）

A、0个 B、1个 C、2个 D、3个

查看试题解析
10. 已知P（2-x，3x-4）到两坐标轴的距离相等，则x的值为（）

A、 $\frac{3}{2}$ B、 $- 1$ C、 $\frac{3}{2}$ 或 $- 1$ D、 $\frac{3}{2}$ 或1

查看试题解析
11. 在“幻方拓展课程”探索中，小明在如图的3×3方格填入了一些表示数的代数式，若图中各行、各列及对角线上的三个数之和都相等，则y﹣x＝（）

A、2 B、4 C、﹣6 D、6

查看试题解析
12. 如图，把半径为0.5的圆放到数轴上，圆上一点A与表示1的点重合，圆沿着数轴滚动一周，此时点A表示的数是（）

A、 $0.5 + π$ 或 $0.5 - π$ B、 $0.25 + π$ 或 $0.25 - π$ C、 $1 + π$ 或 $1 - π$ D、 $2 + π$ 或 $2 - π$

查看试题解析

二、填空题

13. 写出一个比 $\sqrt{3}$ 大且比 $\sqrt{13}$ 小的整数是．

查看试题解析
14. 把一块直尺与一块含30°的直角三角板如图放置，若∠1＝34°，则∠2的度数为．

查看试题解析
15. 在《九章算术》中，二元一次方程组是通过“算筹”摆放的．若图中各行从左到右列出的三组算筹分别表示未知数 $x$ ， $y$ 的系数与相应的常数项，如图1表示方程组是 ${\begin{array}{l} 3 x + 2 y = 19 \\ x + 4 y = 24 \end{array}$ ，则如图2表示的方程组是．

查看试题解析
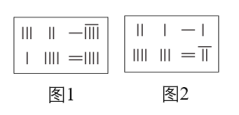16. 数学知识时刻都在应用，比如跳远运动中的成绩问题，如图，有三名同学甲、乙、丙在同一起跳点P处起跳后的落地脚跟为A，B，C，现在只能有两名同学可以参加比赛，不借助其他测量工具，仅仅根据图形和基本数学原理即可确定人选，这里用到的数学原理是.

查看试题解析
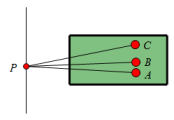17. 中国清代学者华衡芳和英国人傅兰雅合译英国瓦里斯的《代数学》，卷首有“代数之法，无论何数，皆可以任何记号代之”，说明了所谓“代数”，就是用符号来代表数的一种方法，若一个正数的平方根分别是2a﹣3和5﹣a，则这个正数是．

查看试题解析
18. 如图，5个大小形状完全相同的长方形纸片，在直角坐标系中摆成如图图案，已知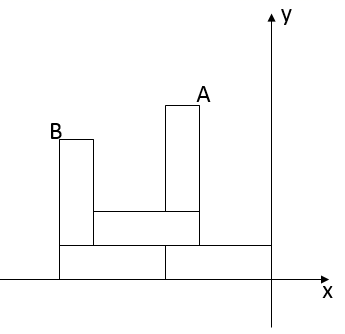 $B (- 8 ， 5)$ ，则点A的坐标为.

查看试题解析

三、解答题

19. 求下列各式中x的值：

(1)、 $\sqrt{0.04} + \sqrt[3]{- 8} - \sqrt{\frac{1}{4}}$ ．

(2)、24（x﹣1）³+3＝0．

查看试题解析
20. 如图，直线AB、CD相交于点O，∠BOD＝40°，按下列要求画图并解答问题：

(1)、利用三角尺，在直线AB上方画射线OE，使∠BOE＝90°；

(2)、利用量角器，画∠AOD的平分线OF；

(3)、在你所画的图形中，求∠AOD与∠EOF的度数．

查看试题解析
21.

(1)、 ${\begin{array}{l} y = 2 x - 3 \\ 3 x + y = 7 \end{array}$

(2)、 ${\begin{array}{l} 5 x + 4 y = 4 \\ 3 x + 2 y = 3 \end{array}$

查看试题解析
22. 如图，点D在BC边上，过D点作DE∥BA交AC于点E，作DF∥CA交AB于点F，请你补全图形，判断∠EDF与∠A的数量关系，并证明你的结论．

查看试题解析
23. 如图，用 $(- 1 ， - 1)$ 表示 $A$ 点的位置，用 $(3 ， 0)$ 表示 $B$ 点的位置．

(1)、画出直角坐标系．

(2)、点 $E$ 的坐标为．

(3)、 $△ C D E$ 的面积为．

查看试题解析
24. 阅读理解：已知实数x，y满足3x﹣y＝5…①，2x+3y＝7…②，求x﹣4y和7x+5y的值．仔细观察两个方程未知数的系数之间的关系，本题可以通过适当变形整体求得代数式的值，比如由①﹣②可得x﹣4y＝﹣2，由①+②×2可得7x+5y＝19．这样的解题思想就是通常所说的“整体思想”．
利用“整体思想”，解决下列问题：

(1)、学以致用：二元一次方程组 ${\begin{array}{l} 2 x + y = 7 \\ x + 2 y = 8 \end{array}$ ，利用“整体思想”求①x﹣y，②x+y．

(2)、拓展提高：买20支铅笔、3块橡皮、2本日记本共需32元；买39支铅笔、5块橡皮3本日记本共需58元，利用“整体思想”求购买5支铅笔、5块橡皮和5本日记本共需多少元？

查看试题解析

25. 本学期《实数》中，我们学习了平方根和立方根，下表是平方根和立方根的部分内容：

	平方根	立方根
定义	一般地，如果一个数x的平方等于a，即x²＝a，那么这个数x就叫做a的平方根（也叫做二次方根）．	一般地，如果一个数x的立方等于a即x＝a，那么这个数x就叫做a的立方根（也叫做三次方根）．
运算	求一个数a的平方根的运算叫做开平方．开平方和平方互为逆运算．	求一个数a的立方根的运算叫做开立方．开立方和立方互为逆运算．
性质	一个正数有两个平方根，它们互为相反数：0的平方根是0；负数没有平方根．	正数的立方根是正数；0的立方根是0；负数的立方根是负数．
表示方法	正数a的平方根可以表示为“± $\sqrt{a}$ ”．	一个数a的立方根可以表示为“ $\sqrt[3]{a}$ ”．

今天我们类比平方根和立方根的学习方法学习四次方根类比探索：

(1)、探索定义：填写下表：

x⁴	1	16	81
x

(2)、探究性质

①1的四次方根是；

②16的四次方根是；

③ $\frac{81}{16}$ 的四次方根是；

④12的四次方根是；

⑤0的四次方根是；

⑥﹣625（填“有”或“没有”）四次方根．

类比平方根和立方根的性质，归纳四次方根的性质：．

(3)、拓展应用：在探索过程中，你用到了哪些数学思想？请写出两个：．

查看试题解析