江西省南昌市校际联盟2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-25 类型:期中考试
一、单选题
-
1. 通过平移,可将图(1)中的福娃“欢欢”移动到图( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 若 , 则为( )A、 B、 C、 D、3. 如图,能判断直线的条件是( )
2. 若 , 则为( )A、 B、 C、 D、3. 如图,能判断直线的条件是( ) A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知点 在 轴上,则点 的坐标是( )A、 B、 C、 D、6. 如图, , , 则、、的关系为( )
A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 已知点 在 轴上,则点 的坐标是( )A、 B、 C、 D、6. 如图, , , 则、、的关系为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 把命题“等角的补角相等”改写成“如果…那么…”的形式是 .8. 已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a= .9.
如图,直线AB、CD相交于点E,DF∥AB.若∠D=65°,则∠AEC=
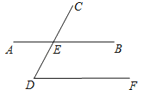 10. 点P(﹣3,4)到x轴的距离是 .11. 已知 , , 若 , 则的值为 .12. 如图,中, , 点是射线上一点(不与点、重合),交直线于 , 交直线于 , 则的度数为 .
10. 点P(﹣3,4)到x轴的距离是 .11. 已知 , , 若 , 则的值为 .12. 如图,中, , 点是射线上一点(不与点、重合),交直线于 , 交直线于 , 则的度数为 .
三、解答题
-
13. 计算:(1)、;(2)、 .14. 若与是同一个正数的平方根,求的值.15. 如图,AB和CD相交于点O,∠DOE=90°,若∠BOE= ∠AOC.
 (1)、指出与∠BOD相等的角,并说明理由;(2)、求∠BOD,∠AOD的度数.16. 在如图所示的平面直角坐标系中,描出下列各点,并将各点用线段依次连接起来:(0,-4),(3,-5),(6,0),(0,-1),(-6,0),(-3,-5),(0,-4).
(1)、指出与∠BOD相等的角,并说明理由;(2)、求∠BOD,∠AOD的度数.16. 在如图所示的平面直角坐标系中,描出下列各点,并将各点用线段依次连接起来:(0,-4),(3,-5),(6,0),(0,-1),(-6,0),(-3,-5),(0,-4). 17. 完成下面的证明.已知:如图,、、分别是 , , 上的点, , . 求证: .
17. 完成下面的证明.已知:如图,、、分别是 , , 上的点, , . 求证: .证明:∵(已知),
∴ ▲ ( ▲ ).
∵(已知);
∴ ▲ = ▲ ( ▲ );
∴( ▲ ).
 18. 已知当、都是实数.且满足时,称为“开心点”.(1)、判断点是否为“开心点”,并说明理由;(2)、若是“开心点”,请判断点在第几象限?并说明理由.19. 已知: 的立方根是 , 的算术平方根3, 是 的整数部分.(1)、求 的值;(2)、求 的平方根.20. 如图,直线CD与直线AB相交于C,根据下列语句画图、解答.
18. 已知当、都是实数.且满足时,称为“开心点”.(1)、判断点是否为“开心点”,并说明理由;(2)、若是“开心点”,请判断点在第几象限?并说明理由.19. 已知: 的立方根是 , 的算术平方根3, 是 的整数部分.(1)、求 的值;(2)、求 的平方根.20. 如图,直线CD与直线AB相交于C,根据下列语句画图、解答.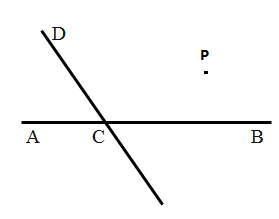 (1)、过点P作PQ∥CD,交AB于点Q;(2)、过点P作PR⊥CD,垂足为R;(3)、若∠DCB=120°,猜想∠PQC是多少度?并说明理由21. 已知三角形与三角形在平面直角坐标系中的位置如图
(1)、过点P作PQ∥CD,交AB于点Q;(2)、过点P作PR⊥CD,垂足为R;(3)、若∠DCB=120°,猜想∠PQC是多少度?并说明理由21. 已知三角形与三角形在平面直角坐标系中的位置如图 (1)、分别写出点、的坐标: , ;(2)、若点是三角形内部一点,则平移后三角形内的对应点的坐标为;(3)、求三角形的面积.22. 先阅读第(1)题的解法,再解答第(2)题:(1)、已知a,b是有理数,并且满足等式 , 求a,b的值.(2)、已知x,y是有理数,并且满足等式 , 求 的值.23. 如图,两个形状,大小完全相同的含有30°、60°的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
(1)、分别写出点、的坐标: , ;(2)、若点是三角形内部一点,则平移后三角形内的对应点的坐标为;(3)、求三角形的面积.22. 先阅读第(1)题的解法,再解答第(2)题:(1)、已知a,b是有理数,并且满足等式 , 求a,b的值.(2)、已知x,y是有理数,并且满足等式 , 求 的值.23. 如图,两个形状,大小完全相同的含有30°、60°的三角板如图放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转. (1)、①如图1,∠DPC= ▲ 度.
(1)、①如图1,∠DPC= ▲ 度.②我们规定,如果两个三角形只要有一组边平行,我们就称这两个三角形为“孪生三角形”,如图1,三角板BPD不动,三角板PAC从图示位置开始每秒10°逆时针旋转一周(0°旋转360°),问旋转时间t为多少时,这两个三角形是“孪生三角形”.
(2)、如图3,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速3°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速2°/秒,在两个三角板旋转过程中,(PC转到与PM重合时,两三角板都停止转动).设两个三角板旋转时间为t秒,以下两个结论:①为定值;②∠BPN+∠CPD为定值,请选择你认为对的结论加以证明.