江西省九江市2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-25 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 ${(a b)}^{4} = a^{4} b^{4}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(a^{3})}^{4} = a^{7}$

查看试题解析
2. 下列算式能用平方差公式计算的是（）

A、 $(3 a + b) (3 b - a)$ B、 $(\frac{1}{3} - 1) (- \frac{1}{3} - 1)$ C、 $(x - y) (- x + y)$ D、 $(- a - b) (a + b)$

查看试题解析
3. 在实验课上，小亮利用同一块木板测得小车从不同高度（h）与下滑的时间（t）的关系如下表：
支撑物高h（cm）
10
20
30
40
50
…
下滑时间t（s）
3.25
3.01
2.81
2.66
2.56
…
以下结论不正确的是（）

A、当h＝40时，t约2.66秒 B、随高度增加，下滑时间越来越短 C、估计当h＝80cm时，t一定小于2.56秒 D、高度每增加了10cm，时间就会减少0.24秒

查看试题解析
4. 如果 $(x - 3) (x + 2) = x^{2} - p x + q$ ，那么p、q的值是（）

A、p=5， q=6 B、p=－1， q=－6 C、p=1， q=－6 D、p=－5， q=－6

查看试题解析
5. 把一块直尺与一块含 $30 °$ 的直角三角板如图放置，若 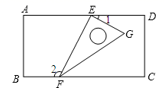$∠ 1 = 34 °$ ，则 $∠ 2$ 的度数为（）

A、 $114 °$ B、 $126 °$ C、 $116 °$ D、124°

查看试题解析
6. 下列选项中，不是运用“垂线段最短”这一性质的是（）

A、立定跳远时测量落点后端到起跳线的距离 B、从一个村庄向一条河引一条最短的水渠 C、把弯曲的公路改成直道可以缩短路程 D、直角三角形中任意一条直角边的长度都比斜边短

查看试题解析
7. 打开某洗衣机开关，在洗涤衣服时（洗衣机内无水），洗衣机经历了进水、清洗、排水、脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量y（升）与时间x（分钟）之间满足某种关系，其关系图象大致为（）

A、 B、 C、 D、

查看试题解析

二、填空题

8. 如图a是长方形纸带，∠DEF=26°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是.

查看试题解析
9. 计算：已知 $a^{m} = 3$ ， $a^{n} = 4$ ，则 $a^{m + n}$ 的值为．

查看试题解析
10. 如图是一把剪刀，若∠AOB+∠COD＝80°，则∠AOC＝度．

查看试题解析
11. 因对新一代基因编辑技术CRISPR的贡献，法国生物化学家埃马纽埃尔·沙尔捷、英国生物学家詹妮弗·杜德纳共同获得了2020年诺贝尔化学奖，CRISPR/Cas9蛋白可以通过剪断病毒DNA的方式“打败”病毒，这在医学上有着重要的意义，已知某病毒DMA分子的直径只有 $0.00000021 m$ ，将0.00000021用科学记数法表示为．

查看试题解析
12. 一个圆的半径长为 $r (r > 2) c m$ ，如果半径减少 $2 c m$ ，那么这个圆的面积减少值 $y (c m^{2})$ 与 $r (c m)$ 的关系式是．

查看试题解析
13. 已知一个角的补角是这个角的余角的3倍，则这个角是度.

查看试题解析
14. 已知 $x - y = 2$ ， $x y = 3$ ，则 $x^{2} + y^{2}$ 的值为.

查看试题解析
15. 如图， $∠ B + ∠ B C D = 180 °$ ， $∠ D = 80 °$ ， $∠ C A D ： ∠ B A C = 3 ： 2$ ，则 $∠ C A D =$ ．

查看试题解析
16. 某段铁路两旁安置了两座可旋转探照灯，主道路是平行，即PQ∥MN．如图所示，灯A射线从AM开始顺时针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是每秒2度，灯B转动的速度是每秒1度．若灯B射线先转动30秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动秒，两灯的光束互相平行．

查看试题解析

三、解答题

17. 计算： $(- 1)^{2012} + {(- \frac{1}{2})}^{- 2} - (2021 - 1)^{0}$

查看试题解析
18. 先化简，再求值： $x (x - 4 y) + (2 x + y) (2 x - y) - {(2 x - y)}^{2}$ ，其中 $x = - 2$ ， $y = - \frac{1}{2}$ ．

查看试题解析
19. 按要求用尺规作图（保留作图痕迹）并填空：如图，点 $O$ 是 $∠ A B C$ 的边 $B A$ 上一点，过点 $O$ 作直线 $O D$ ，使 $O D / / B C$ ．你的作图方法使 $O D / / B C$ 的依据是．

查看试题解析
20. 星期天，小亮的爸爸9点钟从家里到附近的一个银行办理业务，他走了一段路后，突然发现忘记带身份证，于是他跑步回家，拿了身份证，跑到银行办理业务，办完业务他步行回到家．他离家的路程 $s$ （米）与时间 $t$ （分）之间的关系如图所示．

(1)、在上述变化的过程中，自变量是，因变量是；小亮的家距离银行米，小亮爸爸在银行办理业务花了分钟．

(2)、求小亮爸爸从银行回到家的速度．

查看试题解析
21. 如图直线 $E F$ 分别交 $A B$ 、 $C D$ 于点 $M$ 、 $N$ ， $∠ C N F = 40 °$ ， $M G$ 平分 $∠ B M N$ ，交 $C D$ 于点 $G$ ， $∠ B M N = 140 °$ ．

(1)、请说明 $A B / / C D$ ；

(2)、求 $∠ M G N$ ．

查看试题解析
22. 如图1，边长为 $a$ 的大正方形中有一个边长为 $b$ 的小长方形，小亮将阴影部分拼成一个长方形（如图2）．

(1)、上述操作能验证的等式是；

(2)、应用（1）中的等式，完成下列各题：
①已知 $4 x^{2} - y^{2} = 16$ ， $2 x + y = 8$ ，求 $2 x - y$ 的值．
②计算： $(1 + \frac{1}{2}) (1 + \frac{1}{2^{2}}) (1 + \frac{1}{2^{4}}) (1 + \frac{1}{2^{8}}) (1 + \frac{1}{2^{16}}) (1 + \frac{1}{2^{32}})$ ．

查看试题解析
23. 有若干张长为 $30 c m$ 、宽为 $15 c m$ 的长方形白纸，按如图所示的方法黏合起来，黏合部分宽为 $3 c m$ ．

(1)、根据上图，将表格补充完整：
白纸张数
1
2
3
4
…
10
…
纸条长度
30
84
111
…
…

(2)、设 $x$ 张白纸黏合后的总长度为 $y c m$ ，则 $y$ 与 $x$ 之间的关系式是什么?

(3)、按照上述黏合方式，你认为至少需要多少张白纸，才能使得黏合起来总长度达到或超过 $2021 c m$ ?

查看试题解析
24. 在数学实践活动课上，小亮同学利用一副三角尺探索与研究共直角顶点的两个直角三角形中的位置关系与数量关系．（其中 $∠ A = 30 °$ ， $∠ B = 60 °$ ， $∠ C = ∠ D = 45 °$ ）

(1)、将三角尺如图1所示叠放在一起．
① $∠ A O D$ 与 $∠ B O C$ 大小关系是，依据是．
② $∠ B O D$ 与 $∠ A O C$ 的数量关系是．

(2)、小亮固定其中一块三角尺 $△ C O D$ 不变，绕点 $O$ 顺时针转动另一块三角尺，从图2的 $O A$ 与 $O C$ 重合开始，到图3的 $O A$ 与 $O C$ 在一条直线上时结束．探索 $△ A O B$ 的一边与 $△ C O D$ 的一边平行的情况．
①求当 $A B / / C D$ 时，如图4所示， $∠ A O C$ 的大小．
②直接写出 $∠ A O C$ 的其余所有可能值．

查看试题解析

支撑物高h（cm）	10	20	30	40	50	…
下滑时间t（s）	3.25	3.01	2.81	2.66	2.56	…