江西省景德镇市乐平市2020-2021学年七年级下学期期中数学试题
试卷更新日期：2022-03-25 类型：期中考试
一、单选题
-
1. 下列图形中，∠1和∠2是对顶角的是（ ）A、
B、
C、
D、
2. PM25是指大气中直径小于或等于2.5微米的颗粒物，2.5微米等于0.0000025米，把0.0000025用科学记数法表示为（ ）A、2.5×106 B、0.25×10﹣5 C、2.5×10﹣6 D、0.25×10﹣73. 下列运算结果正确的是（ ）A、a2•a3＝a6 B、a+a2＝a3 C、a2÷a＝a D、a2﹣a＝a4. （1+2y）（1﹣2y）计算正确的是（ ）A、1﹣2y2 B、1﹣4y2 C、1﹣y2 D、1﹣4y+4y25. 星期一学校举行升国旗仪式，下列图象能反映国旗高h与时间t的关系的是（ ）A、
B、
C、
D、
6. 如图，直线a，b被直线c所截，∠α同位角是（ ）
A、∠1 B、∠2 C、∠3 D、∠47. 如图，直线AB∥CD，∠1＝110°，则∠A的度数为（ ）
A、70° B、110° C、60° D、100°8. 下表列出了一项实验的统计数据，表示皮球从高处自由落下时，弹跳高度b（cm）与下落时的高度d（cm）之间的关系，那么下面的式子能表示这种关系的是（ ）d（cm）
50
80
100
150
b（cm）
25
40
50
75
A、b＝d2 B、b＝2d C、b＝ D、b＝d+259. 已知a+b＝3，ab＝1，则a2+b2的值为（ ）A、11 B、10 C、8 D、710. 某地区，为了节约用水，采用了分段收水费的办法：每户居民月用水量不超过7吨的按a元/吨收费；月用水量超过7吨的，其中7吨按a元/吨收费，超过部分按b元/吨收费设该地某户月用水量x（吨），应缴水费y（元）y与x关系如图所示某户今年2月份用水15吨，应缴水费是（ ）
A、42元 B、35元 C、45元 D、54元二、填空题
-
11. 计算：（6a2+3a）÷（3a）＝ ．12. 如图，已知直线a∥b，∠1＝130°，则∠2的度数为 ．
13. 某电影院第x排的座位数为y个，y与x的关系如表格所示，第10排的座位数为 ．x
1
2
3
4
5
……
y
23
25
27
29
31
……
14. 如图，l1∥l2 ， 等边△ABC顶点A、B分别在l1 ， l2上，∠2＝45°，则∠1度数为 ．
15. 一根蜡烛燃烧过程中，剩余蜡烛长y（厘米）和燃烧时间x（小时）的关系如图所示，则这根蜡烛燃烧4小时，剩余蜡烛长为厘米．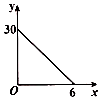
16. 如果（x﹣1）（3x+m）的积中不含x的一次项，则常数m的值为 ．17. 如图，将长方形纸片ABCD沿直线EF折叠，使点C、D落在原长方形平面内的点C′上和点D′上，若∠1＝70°，则∠2的度数为 ．
18. 小贤做题：19×20 ， 他写成19×20＝（a﹣b）（a+b）的形式，利用平方差公式计算就非常简便，则a＝ ， b＝ ．三、解答题
-
19. 直接写出计算结果：(1)、x2•x5；(2)、（x3）2；(3)、（a+b）（a﹣b）．20. 计算：(1)、；(2)、（﹣2x2）•（x2）3÷（﹣x）5 ．21. 先化简，再求值：2x2﹣（﹣2x+3 y）（﹣2x﹣3y）﹣（x﹣3y）2 ， 其中x＝ ， y＝ ．22. 如图，已知直线CD∥AB，OD平分∠BOC，∠2＝50°，求∠1的度数．
23. 如图，AB与CD相交于点O，AE⊥CD且AE平分∠OAC，BF⊥CD且BF平分∠OBD，试说明∠C＝∠D，将下列证明过程补充完整：∵AE⊥CD，BF⊥CD（已知），
∠AEO＝90°，∠BFO＝90°（ ▲ ），
∴∠AED＝∠BFO，
∴AE∥BF（ ▲ ），
∴∠EAO＝∠FBO（两直线平行，内错角相等）．
∵AE平分∠OAC，BF平分∠OBD（已知），
∴∠CAO＝2∠EAO，∠DBO＝2∠FBO（角平分线的定义），
∠CAO＝∠DBO，
∴AC∥BD（ ▲ ），
∴∠C＝∠D（ ▲ ．
24. 一天早上，王大伯挑了一担自己种的土豆到集市卖，他自带了一些零钱备用先按市场价卖出大部分士豆后其余的土豆每千克降价1元全部卖完他持有的y（元）与卖出的土豆x（千克）关系图象如图所示：
(1)、他自带的零钱是 元；(2)、降价前卖出土豆每千克多少元？(3)、这天王大伯共卖了多少千克的土豆？25. 如图①是一个长为2m，宽为2n的长方形（m＞n），用剪刀沿图中虚线剪开，把得到的四块相同的长方形按图2那样拼成一个正方形．
(1)、图②中，中间的小正方形（阴影部分）的边长为 （用含m、n的式子表示）；(2)、观察图②，可得到（m+n）2、（m﹣n）2和4mn之间的等量关系，请直接写出这个等量关系式；(3)、若m+n＝5，mn＝ ， 利用（2）的关系式求（m﹣n）2的值．26. 慧慧和甜甜上山游玩，慧慧乘坐缆车，甜甜步行，两人相约在山顶的缆车终点会合，已知甜甜行走到缆车终点的路程是缆车到山顶的线路长的2倍，慧慧在甜甜出发后50分才乘上缆车，缆车的平均速度为180米/分．设甜甜出发x分后行走的路程为y 米．图中的折线表示甜甜在整个行走过程中y随x的变化关系．
(1)、甜甜行走的总路程是米，她途中休息了分．(2)、分别求出甜甜在休息前和休息后所走的路程段上的步行速度．(3)、当慧慧到达缆车终点时，甜甜离缆车终点的路程是多少．27. 如图，AB∥CD，∠C＝50°，点P是射线CD上一个动点（不与点C重合），点E、F都在射线CD上，AE平分∠CAP，AF平分∠BAP．
(1)、求∠EAF的度数；(2)、①当∠CAP＝20°时，∠1＝ ▲ ， ∠2＝ ▲ ；②当∠CAP＝50°时，∠1＝ ▲ ， ∠2＝ ▲ ；
③当∠CAP＝60°时，∠1＝ ▲ ，∠2＝ ▲ ；
④猜想∠1和∠2的数量关系写出一个等量关系式，并说明理由；
(3)、设∠CAP＝x°时，∠AEF＝y°，①求y与x的关系式；
②当△ACP为直角三角形时，求y的值．