江西省抚州市南丰县2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-25 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $a^{6} \cdot a^{2}$ 的结果是（）

A、 $a^{3}$ B、 $a^{4}$ C、 $a^{8}$ D、 $a^{12}$

查看试题解析
2. 下列代数运算正确的是（）

A、 $x \cdot x^{6} = x^{6}$ B、 ${(x y^{2})}^{3} = x^{3} y^{6}$ C、 ${(x + 2)}^{2} = x^{2} + 4$ D、 $(2 x^{2} - y) (2 x^{2} + y) = 2 x^{4} - y^{2}$

查看试题解析
3. 已知 $4^{m} = a$ ， $8^{n} = b$ ，其中 $m$ ， $n$ 为正整数，则 $2^{2 m + 6 n} =$ （）

A、 $a b^{2}$ B、 $a + b^{2}$ C、 $a^{2} b^{3}$ D、 $a^{2} + b^{3}$

查看试题解析
4.
如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）

A、30° B、25° C、20° D、15°

查看试题解析
5. 弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂重物的质量x（kg）有下面的关系，那么弹簧总长y（cm）与所挂重物x（kg）之间的关系式为（）

x（kg）

0

1

2

3

4

5

6

y（cm）

12

12.5

13

13.5

14

14.5

15

A、y=0.5x+12 B、y=x+10.5 C、y=0.5x+10 D、y=x+12

查看试题解析
6. 如图，在 $Δ A B C$ 中， $A C = B C$ ，若有一动点P从A出发，沿 $A \to C \to B \to A$ 匀速运动，则 $C P$ 的长度s与时间t之间的关系用图像表示大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 函数 $y = \frac{1}{2 x - 1}$ 中，自变量x的取值范围是．

查看试题解析
8. 已知 ${(9^{n})}^{2} = 3^{8}$ ，则 n= .

查看试题解析
9. 某微生物的直径为0.000 005 035m ，用科学记数法表示该数为．

查看试题解析
10. 若∠1与∠2互补，∠3与30°互余，∠2+∠3=210°，则∠1=度．

查看试题解析
11. 定义一种新运算 $A$ ※ $B = A^{2} + A B$ 例如 $(- 2)$ ※ $5 = (- 2)^{2} + (- 2) \times 5 = - 6$ ．按照这种运算规定，当 $(x + 2)$ ※ $(2 - x) = 10$ 时，则 $x =$ ．

查看试题解析
12. 若（m-2）^㎡-9=1，则符合条件的 $m$ 有．

查看试题解析

三、解答题

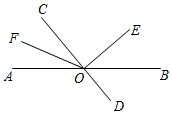
13.

(1)、用乘法公式计算： $19 9^{2} - 199 \times 201$ ．

(2)、计算： ${(- 1)}^{2018} - {(3 - π)}^{0} + {(- \frac{1}{3})}^{- 2}$ ．

查看试题解析
14. 先化简，再求值： ${(2 m + n)}^{2} - (2 m - n) (m + n) - 2 (m - 2 n) (m + 2 n)$ ，其中 $m = - \frac{1}{2}$ ，n=2.

查看试题解析
15. 如图，直线AB与CD相交于点O， $E O ⊥ C D$ 于点O，OF平分 $∠ A O C$ ．若 $∠ B O E$ ： $∠ A O C$ =4：5，求 $∠ E O F$ 的度数

查看试题解析
16. 已知 ${(a + b)}^{2} = 5$ ， ${(a - b)}^{2} = 3$ ，求下列式子的值：

(1)、 $a^{2} + b^{2}$ ；

(2)、6ab.

查看试题解析
17. 小安的一张地图上有A，B，C3三个城市，地图上的C城市被墨污染了（如图），但知道∠BAC=∠α，∠ABC=∠β，你能用尺规作图帮他在下图中确定C城市的具体位置吗？（不作法，保留作图痕迹）

查看试题解析
18. 王老师家买了一套新房，其结构如图所示(单位：m)．他打算将卧室铺上木地板，其余部分铺上地砖．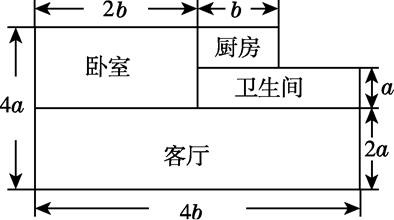

(1)、木地板和地砖分别需要多少平方米？

(2)、如果地砖的价格为每平方米x元，木地板的价格为每平方米3x元，那么王老师需要花多少钱？

查看试题解析
19. 补充完成下面的推理过程．
如图，已知点 $D ， E ， F$ 分别是 $Δ A B C$ 的边 $B C ， A C ， A B$ 上的点， $D E / / A B ， D F / / A C$ ．

求证： $∠ F D E = ∠ A$ ．

证明： $∵ D E / / A B$ ，（已知）

$∴ ∠ F D E =$                   ▲                  （                  ▲                  ）

$∵ D F / / A C ，$ （                   ▲                  ）

$∴ ∠ A =$                   ▲                  （                  ▲                  ）

$∴$                   ▲                   $=$                   ▲                  （                  ▲                  ）

查看试题解析
20. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F.

(1)、CD与EF平行吗？为什么？

(2)、如果∠1＝∠2，试判断DG与BC的位置关系，并说明理由.

查看试题解析
21. 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”（如图），此图揭示了 $(a + b)^{n}$ （ $n$ 为非负整数）展开式的项数及各项系数的有关规律，例如： $(a + b)^{0} = 1$ ，它只有一项，系数为 $1$ ； $(a + b)^{1} = a + b$ ，它有两项，系数分别为 $1$ ， $1$ ，系数和为 $2$ ； $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ，它有三项，系数分别为 $1$ ， $2$ ， $1$ ，系数和为 $4$ ； $(a + b)^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ ，它有四项，系数分别为 $1$ ， $3$ ， $3$ ， $1$ ，系数和为 $8$ ； $⋯$
$1$
$1$         $1$
$1$         $2$         $1$
$1$         $3$          $3$          $1$
根据以上规律，解答下列问题：

(1)、 $(a + b)^{4}$ 的展开式共有项，系数分别为．

(2)、 $(a + b)^{n}$ 的展开式共有项，系数和为．

(3)、计算： $2^{5} + 5 \times 2^{4} + 10 \times 2^{3} + 10 \times 2^{2} + 5 \times 2 + 1$ ．

查看试题解析
22. 周末，小明坐公交车到滨海公园游玩，他从家出发0.8小时后达到中心书城，逗留一段时间后继续坐公交车到滨海公园，小明离家一段时间后，爸爸驾车沿相同的路线前往海滨公园.如图是他们离家路程s（km）与小明离家时间t（h）的关系图，请根据图回答下列问题：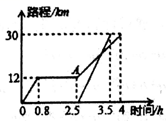

(1)、图中自变量是，因变量是；

(2)、小明家到滨海公园的路程为km，小明在中心书城逗留的时间为h；

(3)、小明出发小时后爸爸驾车出发；

(4)、图中A点表示；

(5)、小明从中心书城到滨海公园的平均速度为km/h，小明爸爸驾车的平均速度为km/h；（补充；爸爸驾车经过追上小明）；

(6)、小明从家到中心书城时，他离家路程s与坐车时间t之间的关系式为.

查看试题解析
23. 已知，直线AB∥CD．

(1)、如图1，点E在直线BD的左侧，猜想∠ABE、∠CDE、∠BED的数量关系，并证明你的结论；

(2)、如图2，点E在直线BD的左侧，BF、DF分别平分∠ABE、∠CDE，猜想∠BFD和∠BED的数量关系，并证明你的结论；

(3)、如图3，点E在直线BD的右侧，BF、DF分别平分∠ABE、∠CDE，那么第（2）问中∠BFD和∠BED的数量关系的猜想是否仍成立？如果成立，请证明；如果不成立，请写出你的猜想，并证明．

查看试题解析

x（kg）	0	1	2	3	4	5	6
y（cm）	12	12.5	13	13.5	14	14.5	15