江西省抚州市东乡区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-25 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，直线 $a$ // $b$ ， $∠ 1 ＝ 48 °$ ，则 $∠ 2$ 等于（）

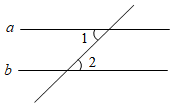A、24° B、42° C、48° D、132°

查看试题解析
2. 二十四节气是中国古代劳动人民长期经验积累的结晶，它与白昼时长密切相关．当春分、秋分时，昼夜时长大致相等；当夏至时，白昼时长最长，根据如图，在下列选项中指出白昼时长不足11小时的节气（）

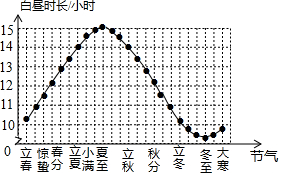A、惊蛰 B、小满 C、立秋 D、大寒

查看试题解析
3. 下列计算正确的是（）

A、 $3 a \cdot a^{3} = 3 a^{3}$ B、 $a^{3} \div a = a^{2}$ C、 $(a + 2)^{2} = a^{2} + 4$ D、 ${(2 a^{2})}^{3} = 6 a^{6}$

查看试题解析
4. 如图，直线 $a ， b$ 被直线 $c ， d$ 所截下列条件能判定 $a / / b$ 的是（）

A、 $∠ 1 = ∠ 3$ B、 $∠ 2 + ∠ 4 = 180^{\circ}$ C、 $∠ 4 = ∠ 5$ D、 $∠ 1 = ∠ 2$

查看试题解析
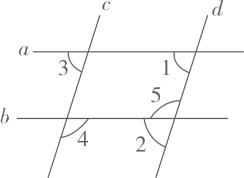5. 在某次实验中，测得两个变量m和v之间的4组对应数据如下表：则m与v之间的关系最接近于下列各关系式中的（　　）
m
1
2
3
4
v
0.01
2.9
8.03
15.1

A、v=2m﹣2 B、v=m²﹣1 C、v=3m﹣3 D、v=m+1

查看试题解析
6. 将图甲中阴影部分的小长方形变换到图乙位置，从图形的面积关系得到的数学公式是（）

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 $a^{2} - a b = a (a - b)$

查看试题解析

二、填空题

7. 计算： ${(- \frac{1}{2})}^{- 1}$ = ．

查看试题解析
8. 2020年6月23日9时43分，“北斗三号”最后一颗全球组网卫星发射成功，它的授时精度小于 $0.00000002$ 秒，则 $0.00000002$ 用科学记数法表示为．

查看试题解析
9. 自变量x与因变量y的关系如图，当x每增加1时，y增加；

查看试题解析
10. 如图， $A B / / C D$ ， $A B ⊥ A E$ ， $∠ C A E = 42^{\circ}$ ，则 $∠ A C D$ 的度数为．

查看试题解析
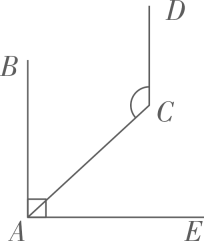11. 张大妈购进一批柚子，在集贸市场零售，已知卖出的柚子重量 $x (k g)$ 与售价y（元）之间的关系如下表：
重量/ $k g$
1
2
3
…
售价/元
$1.2 + 0.1$
$2.4 + 0.1$
$3.6 + 0.1$
…
根据表中数据可知，若一次售价10.9元，则这次卖出柚子 $k g$ ．

查看试题解析
12. 一副直角三角尺叠放如图1所示，现将 $45 °$ 的三角尺 $A D E$ 固定不动，将含 $30 °$ 的三角尺 $A B C$ 绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行．如图2：当 $∠ C A E = 60 °$ 时， $B C / / D E$ ．则 $∠ C A E (0 ° < ∠ C A E < 180 °)$ 其它所有可能符合条件的度数为．

查看试题解析

三、解答题

13.

(1)、计算： ${(- 2 a^{3})}^{2} + {(- a^{2})}^{3}$ ．

(2)、如图，平行线 $A B ， C D$ 被直线 $A E$ 所截， $∠ 2 = 110 °$ ，求 $∠ 1$ 的度数．

查看试题解析
14. 如图，已知 $∠ 1 ， ∠ 2 (∠ 1 > ∠ 2)$ ，利用尺规作图，求作： $∠ A O B = ∠ 1 - ∠ 2$ ．（保留作图痕迹，不写作法）

查看试题解析
15. 为了解某品牌轿车的耗油情况，将油箱加满后进行了耗油试验，得到如表数据：
轿车行驶的路程 $s (k m)$
0
100
200
300
400
…
油箱剩余油量 $Q (L)$
50
42
34
26
18
…

(1)、该轿车油箱的容量为L，行驶 $250 k m$ 时，油箱剩余油量为L；

(2)、根据上表数据，写出油箱剩余油量 $Q (L)$ 与轿车行驶的路程 $s (k m)$ 之间的表达式．

查看试题解析
16. 完成下面的证明．
已知：如图， $A B / / C D ， B E$ 交 $C D$ 于点M， $∠ B = ∠ D$ ．
求证： $B E / / D F$ ．
证明：∵ $A B / / C D$ ，
∴ $∠ B =$                   ▲                  （                  ▲                  ），
∵ $∠ B = ∠ D$ ，
∴                  ▲                   $= ∠ D$ ，
∴                  ▲                   $/ /$                   ▲                  （                  ▲                  ）．

查看试题解析
17. 先化简，再求值： $(- x - 2 y) (2 y - x) + (x + 2 y)^{2} - x (2 y - x)$ ，其中 $x = - \frac{1}{3} ， y = 3$ ．

查看试题解析
18. 如图， $∠ A B C = 50 °$ ， D是 $B A$ 边上一点， $D E / / B C$ ， $D F$ 平分 $∠ B D E$ ，交 $B C$ 于F．

(1)、 $∠ B D E =$ ；

(2)、依题意补全图形并求 $∠ D F B$ 的度数．

查看试题解析
19. 如图，某小区有一块长为 $(2 a + 4 b)$ 米，宽为 $(2 a - b)$ 米的长方形地块，角上有四个边长为 $(a - b)$ 米的小正方形空地，开发商计划将阴影部分进行绿化．

(1)、用含有a､b的式子表示绿化的总面积（结果写成最简形式）；

(2)、物业找来“阳光”绿化团队完成此项绿化任务，已知该队每小时可绿化 $8 b$ 平方米，每小时收费200元，则该物业应该支付绿化队多少费用?（用含a､b的代数式表示）

查看试题解析
20. 如图，已知点O在直线AB上，作射线OC ，点D在平面内，∠BOD与∠AOC互余．

(1)、若∠AOC：∠BOD=4：5，则∠BOD=；

(2)、若∠AOC=α(0°<α≤45°)，ON平分∠COD ．
①当点D在∠BOC内，补全图形，直接写出∠AON的值（用含α的式子表示）；

②若∠AON与∠COD互补，求出α的值．

查看试题解析
21. 小明家距离学校8千米，某天早晨，小明骑车上学途中，自行车出现故障，恰好路边有便民服务点，几分钟后车修好了，他以更快的速度匀速骑车到校．如图，描绘了小明行驶的路程（千米）与他所用的时间（分钟）之间的关系．请根据图象，解答下列问题：

(1)、小明行了千米时，自行车出现故障；他从早晨出发直到到达学校共用了分钟；

(2)、小明修车前､后的行驶速度分别是多少?

(3)、如果自行车未出现故障，小明一直用修车前的速度行驶，那么他比实际情况早到或晚到多少分钟?

查看试题解析
22. 数形结合是解决数学问题的一种重要思想方法，借助图的直观性，可以帮助理解数学问题．

(1)、通过两种不同方法表示出图1阴影部分的面积，可验证的乘法公式是．

(2)、如图2，用4个完全相同的长和宽分别为 $a ､ b (a > b)$ 的长方形拼摆成一个正方形，借助图形，请你写出代数式 ${(a + b)}^{2}$ ､ ${(a - b)}^{2}$ ､ $a b$ 之间的等量关系．

(3)、根据（2）中发现的结论，求：当 $a + b = 5 ， a b = - 6$ 时，则 $a - b$ 的值．

查看试题解析
23. 已知 $A M / / N C$ ，点B为平面内一点， $A B ⊥ B C$ 于B．

(1)、如图1， $∠ A + ∠ C =$ $°$ ；

(2)、如图2，过点B作 $B D ⊥ A M$ 于点D，猜测 $∠ A B D$ 与 $∠ C$ 的大小关系，并说明理由；

(3)、如图3，在（2）的条件下，点E､F在 $D M$ 上，连接 $B E$ ､ $B F$ ､ $C F$ ， $B E$ 平分 $∠ A B D$ ，若 $∠ F C B + ∠ N C F = 180 °$ ， $∠ D F C = 3 ∠ E B A$ ，求 $∠ E B C$ 的度数．

查看试题解析

重量/ $k g$	1	2	3	…
售价/元	$1.2 + 0.1$	$2.4 + 0.1$	$3.6 + 0.1$	…

轿车行驶的路程 $s (k m)$	0	100	200	300	400	…
油箱剩余油量 $Q (L)$	50	42	34	26	18	…

m	1	2	3	4
v	0.01	2.9	8.03	15.1