浙江省宁波市镇海区2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2022-03-24 类型:期中考试
一、单选题(共10题;共30分)
-
1. 下列选项中哪一个可以看作是由图案自身的一部分平移后得到的( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各对角中,内错角是哪一对( )
2. 下列各对角中,内错角是哪一对( )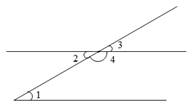 A、∠1和∠3 B、∠1和∠4 C、∠2和∠3 D、∠1和∠23. 下列运算正确的是( )A、 B、 C、 D、4. 下列各式中是二元一次方程的是( )A、 B、 C、 D、5. 如图,直线 那么 的度数是( )
A、∠1和∠3 B、∠1和∠4 C、∠2和∠3 D、∠1和∠23. 下列运算正确的是( )A、 B、 C、 D、4. 下列各式中是二元一次方程的是( )A、 B、 C、 D、5. 如图,直线 那么 的度数是( ) A、70° B、80° C、110° D、130°6. 为了了解某校1200名学生的身高,从中抽取了200名学生对其身高进行统计分析,则下列说法正确的是( )A、1200名学生是总体 B、每个学生是个体 C、200名学生是抽取的一个样本 D、每个学生的身高是个体7. 计算下列各式,其结果为 的是( )A、 B、 C、 D、8. 已知 , ,则 的值是( )A、66 B、65 C、64 D、639. , 则xy的值是( )A、-1 B、1 C、 D、210. 如图,已知AP平分∠BAC,CP平分∠ACD,∠1+∠2 =90°.下列结论正确的有( )
A、70° B、80° C、110° D、130°6. 为了了解某校1200名学生的身高,从中抽取了200名学生对其身高进行统计分析,则下列说法正确的是( )A、1200名学生是总体 B、每个学生是个体 C、200名学生是抽取的一个样本 D、每个学生的身高是个体7. 计算下列各式,其结果为 的是( )A、 B、 C、 D、8. 已知 , ,则 的值是( )A、66 B、65 C、64 D、639. , 则xy的值是( )A、-1 B、1 C、 D、210. 如图,已知AP平分∠BAC,CP平分∠ACD,∠1+∠2 =90°.下列结论正确的有( )① ② ③ ④若 则
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(共8题;共24分)
-
11. 0.025用科学记数法表示:.12. 已知一组数据的样本容量是60,若某一小组的频数是12,则该组的频率是 .13. 将方程2x+y=2变形成用x的代数式表示y,则y= .14. 已知 是方程mx+3y=2的一个解,则m=.15. 如果 的乘积中不含x的一次项,则a=.16. 如图,已知AB∥CD,BF平分∠ABE,BF//DE且∠D=40°则∠BED的度数为.
 17. 已知 则 的值为.18. 如图,把五个长为b、宽为 的小长方形,按图1和图2两种方式放在一个宽为 的大长方形上(相邻的小长方形既无重叠,又不留空隙).设图1中两块阴影部分的周长和为 ,图2中阴影部分的周长为 ,若大长方形的长比宽大 ,则 的值为.
17. 已知 则 的值为.18. 如图,把五个长为b、宽为 的小长方形,按图1和图2两种方式放在一个宽为 的大长方形上(相邻的小长方形既无重叠,又不留空隙).设图1中两块阴影部分的周长和为 ,图2中阴影部分的周长为 ,若大长方形的长比宽大 ,则 的值为.
三、解答题(共7题;共46分)
-
19. 计算:(1)、(2)、20. 解下列方程组(1)、(2)、21. 先化简再求值: ,其中 .22. 如图, 求 的度数.
请完善解答过程,并在括号内填写相应的理论依据.

解:∵ (已知)
∴ ∥ ( )
∴ ( )
∵ (已知)
∴ = .
23. 某校开设了丰富多彩的实践类拓展课程,分别设置了体育类、艺术类、文学类及其他类课程(要求人人参与,每人只能选择一门课程).为了解学生喜爱的拓展类类别,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题: (1)、写出此次抽样调查的样本容量是;(2)、将条形统计图补充完整;(3)、求文学类课程在扇形统计图中所占圆心角的度数;(4)、若该校有1500名学生,请估计喜欢体育类和文学类拓展课的学生总人数.24. 某校准备组织七年级400名学生参加夏令营,已知用1辆小客车和2辆大客车每次可运送学生110人;用4辆小客车和1辆大客车每次可运送学生125人.(1)、每辆小客车和每辆大客车各能坐多少名学生?(2)、若学校计划租用小客车 辆,大客车 辆,一次送完,且恰好每辆车都坐满;
(1)、写出此次抽样调查的样本容量是;(2)、将条形统计图补充完整;(3)、求文学类课程在扇形统计图中所占圆心角的度数;(4)、若该校有1500名学生,请估计喜欢体育类和文学类拓展课的学生总人数.24. 某校准备组织七年级400名学生参加夏令营,已知用1辆小客车和2辆大客车每次可运送学生110人;用4辆小客车和1辆大客车每次可运送学生125人.(1)、每辆小客车和每辆大客车各能坐多少名学生?(2)、若学校计划租用小客车 辆,大客车 辆,一次送完,且恰好每辆车都坐满;①请你设计出所有的租车方案;
②若小客车每辆需租金4000元,大客车每辆需租金7600元,请选出最省钱的租车方案,并求出最少租金.
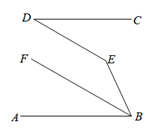
25. 如图, , 定点 , 分别在直线 上,在平行线 之间有一个动点 ,满足 (1)、试问: 满足怎样的数量关系?
(1)、试问: 满足怎样的数量关系?解:由于点 是平行线 之间一动点,因此需对点 的位置进行分类讨论.
如图1,当点 在 的左侧时,
易得 满足的数量关系为 ;
如图2,当点 在 的右侧时,
写出 满足的数量关系.
(2)、如图3,① 的度数为 ▲ ;
②猜想 的数量关系,并说明理由;
③如图4,若 与 的角平分线交于点 , 与 的角平分线
交于点 , 与 的角平分线交于点 ,以此类推,则 与
 满足怎样的数量关系?(直接写出结果)
满足怎样的数量关系?(直接写出结果)