江苏省徐州市2020-2021学年八年级下学期数学期中考试试卷
试卷更新日期:2022-03-24 类型:期中考试
一、单选题
-
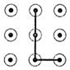
1. 下列手机手势解锁图案中,是中心对称图形的是( )A、
 B、
B、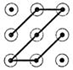 C、
C、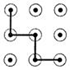 D、
D、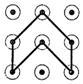 2. “新冠病毒”的英语“NewCoronavirus”中,字母“o”出现的频率是( ).A、 B、1 C、2 D、3. 下列调查中,适宜采用普查方式的是( )A、防疫期间,进入校园要测量体温 B、了解全国八年级学生对新冠肺炎病毒的认知情况 C、考察线上学习期间全市中小学生作业完成情况 D、了解全市中学生在疫情期间的作息情况4. 下列属于必然事件的是( )A、水中捞月 B、水滴石穿 C、守株待兔 D、刻舟求剑5. 抛掷一枚质地均匀的硬币,若抛掷6次都是正面朝上,则抛掷第7次( ).A、正面朝上的可能性大 B、反面朝上的可能性大 C、正面朝上与反面朝上的可能性一样大 D、无法确定6. 菱形的对角线长分别是8,6,则这个菱形的面积是( )A、48 B、24 C、14 D、127. 如图,在中,点、分别是、的中点, , 点是上一点,.连接、 , 若 , 则的长度为( ).
2. “新冠病毒”的英语“NewCoronavirus”中,字母“o”出现的频率是( ).A、 B、1 C、2 D、3. 下列调查中,适宜采用普查方式的是( )A、防疫期间,进入校园要测量体温 B、了解全国八年级学生对新冠肺炎病毒的认知情况 C、考察线上学习期间全市中小学生作业完成情况 D、了解全市中学生在疫情期间的作息情况4. 下列属于必然事件的是( )A、水中捞月 B、水滴石穿 C、守株待兔 D、刻舟求剑5. 抛掷一枚质地均匀的硬币,若抛掷6次都是正面朝上,则抛掷第7次( ).A、正面朝上的可能性大 B、反面朝上的可能性大 C、正面朝上与反面朝上的可能性一样大 D、无法确定6. 菱形的对角线长分别是8,6,则这个菱形的面积是( )A、48 B、24 C、14 D、127. 如图,在中,点、分别是、的中点, , 点是上一点,.连接、 , 若 , 则的长度为( ). A、18 B、16 C、14 D、128. 如图,中, , , .点 , , 分别是边 , , 的中点;点 , , 分别是边 , , 的中点;…以此类推,则第2021个三角形的周长是( ).
A、18 B、16 C、14 D、128. 如图,中, , , .点 , , 分别是边 , , 的中点;点 , , 分别是边 , , 的中点;…以此类推,则第2021个三角形的周长是( ). A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 从一批袋装食品中抽取袋,调查这批食品中防腐剂的含量,在这一抽样调查中,样本容量是.10. 某批篮球的质量检验结果如下:
抽取的篮球数
100
200
400
600
800
1000
1200
优等品的频数
93
192
380
561
752
941
1128
优等品的频率
0.930
0.960
0.950
0.935
0.940
0.940
0.940
从这批篮球中,任意抽取一只篮球是优等品的概率的估计值是.(精确到)
11. “若a2=b2 , 则a=b”这一事件是.(填“必然事件”“不可能事件”或“随机事件”)12. 疫情期间,某地为了描述每天新增“新冠肺炎”人数的变化过程和趋势,适合采统计图.13. 如图,在平行四边形中,的平分线交边于 , 平形四边形的周长是 , , 则=. 14. 如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点G的坐标为.
14. 如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点G的坐标为. 15. 若顺次连接一个四边形各边中点所得的图形为矩形,则这个四边形需要满足的条件为.16. 如图,在中, , , , 为边上一动点,于 , 于 , 连接 , 则的最小值为.
15. 若顺次连接一个四边形各边中点所得的图形为矩形,则这个四边形需要满足的条件为.16. 如图,在中, , , , 为边上一动点,于 , 于 , 连接 , 则的最小值为. 17. 如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF=.
17. 如图,在边长为10的菱形ABCD中,对角线BD=16,点O是线段BD上的动点,OE⊥AB于E,OF⊥AD于F.则OE+OF=.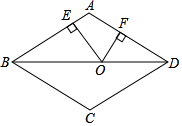 18. 如图,平行四边形中, , , 点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点出发,在间往返运动,两个点同时出发,当点到达点时停止(同时点也停止).在运动以后,当时以、、、四点组成的四边形为平行四边形.
18. 如图,平行四边形中, , , 点在边上以每秒的速度从点向点运动,点在边上,以每秒的速度从点出发,在间往返运动,两个点同时出发,当点到达点时停止(同时点也停止).在运动以后,当时以、、、四点组成的四边形为平行四边形. 19. 一个不透明的袋中装有1个黄球、2个黑球和3个红球,这些球除颜色外都相同,将球摇匀,从中任意摸出1个球.(1)、我认为摸到颜色的球的概率最大;(2)、怎样改变袋子中黄球、黑球和红球的个数,使摸到这三种颜色的球的概率相等?
19. 一个不透明的袋中装有1个黄球、2个黑球和3个红球,这些球除颜色外都相同,将球摇匀,从中任意摸出1个球.(1)、我认为摸到颜色的球的概率最大;(2)、怎样改变袋子中黄球、黑球和红球的个数,使摸到这三种颜色的球的概率相等?三、解答题
-
20. 某校学生会调查了八年级部分学生对“垃圾分类”的了解程度,将收集到的数据绘制成如下图①、图②两幅不完整的统计图,请你根据图中信息,回答下列问题:
 (1)、本次调查学生人数共有名;(2)、补全图①中的条形统计图,图②中“了解一点”的圆心角度数为 ▲ ;(3)、根据本次调查,估计该校八年级500名学生中,“比较了解”垃圾分类的学生大约有名.21. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)、本次调查学生人数共有名;(2)、补全图①中的条形统计图,图②中“了解一点”的圆心角度数为 ▲ ;(3)、根据本次调查,估计该校八年级500名学生中,“比较了解”垃圾分类的学生大约有名.21. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).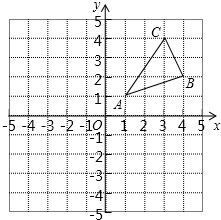 (1)、请画出△ABC关于原点对称的△A1B1C1;(2)、四边形CBC1B1为四边形;(3)、点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.22. 已知点、分别是平行四边形的边、的中点.
(1)、请画出△ABC关于原点对称的△A1B1C1;(2)、四边形CBC1B1为四边形;(3)、点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.22. 已知点、分别是平行四边形的边、的中点. (1)、求证:四边形是平行四边形;(2)、若 , , 求平行四边形的周长.23. 如图,菱形的对角线、相交于点 , , , 与交于点.
(1)、求证:四边形是平行四边形;(2)、若 , , 求平行四边形的周长.23. 如图,菱形的对角线、相交于点 , , , 与交于点. (1)、试判断四边形的形状,并说明理由;(2)、若 , , 求菱形的面积.24. 如图,将矩形 绕点 顺时针旋转 得矩形 , 当点 落在 上时,连接 .求证: .
(1)、试判断四边形的形状,并说明理由;(2)、若 , , 求菱形的面积.24. 如图,将矩形 绕点 顺时针旋转 得矩形 , 当点 落在 上时,连接 .求证: .

