2022年高考物理三轮冲刺练习专题五 静电场和磁场综合计算题
试卷更新日期:2022-03-24 类型:三轮冲刺
一、计算题
-
1. 如图,圆心为O、半径为r的圆形区域外存在匀强磁场,磁场方向垂直于纸面向外,磁感应强度大小为B。P是圆外一点,OP=3r。一质量为m、电荷量为q(q>0)的粒子从P点在纸面内垂直于OP射出。已知粒子运动轨迹经过圆心O,不计重力。求
 (1)、粒子在磁场中做圆周运动的半径;(2)、粒子第一次在圆形区域内运动所用的时间。2.
(1)、粒子在磁场中做圆周运动的半径;(2)、粒子第一次在圆形区域内运动所用的时间。2.一台质谱仪的工作原理如图所示.大量的甲、乙两种离子飘入电压力为U0的加速电场,其初速度几乎为0,经过加速后,通过宽为L的狭缝MN沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片上.已知甲、乙两种离子的电荷量均为+q,质量分别为2m和m,图中虚线为经过狭缝左、右边界M、N的甲种离子的运动轨迹.不考虑离子间的相互作用.
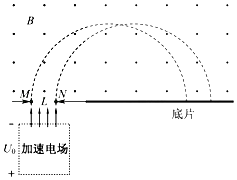 (1)、求甲种离子打在底片上的位置到N点的最小距离x;(2)、在答题卡的图中用斜线标出磁场中甲种离子经过的区域,并求该区域最窄处的宽度d;(3)、若考虑加速电压有波动,在(U0﹣△U)到(U0+△U)之间变化,要使甲、乙两种离子在底片上没有重叠,求狭缝宽度L满足的条件.3.
(1)、求甲种离子打在底片上的位置到N点的最小距离x;(2)、在答题卡的图中用斜线标出磁场中甲种离子经过的区域,并求该区域最窄处的宽度d;(3)、若考虑加速电压有波动,在(U0﹣△U)到(U0+△U)之间变化,要使甲、乙两种离子在底片上没有重叠,求狭缝宽度L满足的条件.3.如图所示,x轴上M点和N点的坐标分别是(0.5 m,0)、(2 m,0),虚线MM′与y轴平行。在y轴和MM′之间加垂直纸面方向的匀强磁场,在N点固定一个正的点电荷 。现有一个质量 、电荷量的大小 的粒子,从y轴上某点沿x轴的正方向以初速度 进入磁场,在第四象限里一直做匀速圆周运动,最后从x轴上的Q点(没画出)射入第一象限,不计带电粒子的重力,粒子在磁场中运动时就不受在N点的固定点电荷影响。已知静电力常量k=9×109 N·m2/C2。求:
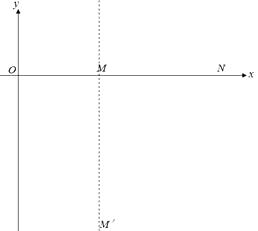 (1)、Q点的坐标;(2)、匀强磁场的磁感应强度的大小和方向;(3)、带电粒子从开始运动到Q点的时间。4. 如图所示,真空中四个相同的矩形匀强磁场区域,高为4d , 宽为d , 中间两个磁场区域间隔为2d , 中轴线与磁场区域两侧相交于O、O′点,各区域磁感应强度大小相等.某粒子质量为m、电荷量为+q , 从O沿轴线射入磁场.当入射速度为v0时,粒子从O上方 处射出磁场.取sin53°=0.8,cos53°=0.6.
(1)、Q点的坐标;(2)、匀强磁场的磁感应强度的大小和方向;(3)、带电粒子从开始运动到Q点的时间。4. 如图所示,真空中四个相同的矩形匀强磁场区域,高为4d , 宽为d , 中间两个磁场区域间隔为2d , 中轴线与磁场区域两侧相交于O、O′点,各区域磁感应强度大小相等.某粒子质量为m、电荷量为+q , 从O沿轴线射入磁场.当入射速度为v0时,粒子从O上方 处射出磁场.取sin53°=0.8,cos53°=0.6. (1)、求磁感应强度大小B;(2)、入射速度为5v0时,求粒子从O运动到O′的时间t;(3)、入射速度仍为5v0 , 通过沿轴线OO′平移中间两个磁场(磁场不重叠),可使粒子从O运动到O′的时间增加Δt , 求Δt的最大值.5. 真空中存在电场强度大小为E1的匀强电场,一带电油滴在该电场中竖直向上做匀速直线运动,速度大小为v0 , 在油滴处于位置A时,将电场强度的大小突然增大到某值,但保持其方向不变.持续一段时间t1后,又突然将电场反向,但保持其大小不变;再持续同样一段时间后,油滴运动到B点.重力加速度大小为g.(1)、油滴运动到B点时的速度;(2)、求增大后的电场强度的大小;为保证后来的电场强度比原来的大,试给出相应的t1和v0应满足的条件.已知不存在电场时,油滴以初速度v0做竖直上抛运动的最大高度恰好等于B、A两点间距离的两倍.6.
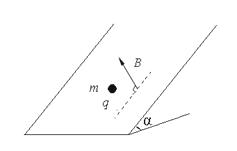
(1)、求磁感应强度大小B;(2)、入射速度为5v0时,求粒子从O运动到O′的时间t;(3)、入射速度仍为5v0 , 通过沿轴线OO′平移中间两个磁场(磁场不重叠),可使粒子从O运动到O′的时间增加Δt , 求Δt的最大值.5. 真空中存在电场强度大小为E1的匀强电场,一带电油滴在该电场中竖直向上做匀速直线运动,速度大小为v0 , 在油滴处于位置A时,将电场强度的大小突然增大到某值,但保持其方向不变.持续一段时间t1后,又突然将电场反向,但保持其大小不变;再持续同样一段时间后,油滴运动到B点.重力加速度大小为g.(1)、油滴运动到B点时的速度;(2)、求增大后的电场强度的大小;为保证后来的电场强度比原来的大,试给出相应的t1和v0应满足的条件.已知不存在电场时,油滴以初速度v0做竖直上抛运动的最大高度恰好等于B、A两点间距离的两倍.6.如图所示,固定在水平面上的斜面倾角为α,磁感应强度为B的匀强磁场垂直于斜面向上。将质量为m、带电量为+q的滑块轻轻放置在斜面上,求滑块稳定滑动时速度的大小和方向(与图中虚线之间的夹角)(斜面与滑块之间的动摩擦因数 )
 7.
7.如图所示,质量为m,电荷量为q的带电粒子,以初速度v沿垂直磁场方向射入磁感应强度为B的匀强磁场,在磁场中做匀速圆周运动。不计带电粒子所受重力。

①求粒子做匀速圆周运动的半径R和周期T;
②为使该粒子做匀速直线运动,还需要同时存在一个与磁场方向垂直的匀强电场,求电场强度E的大小。
8.回旋加速器的工作原理如题15-1图所示,置于真空中的D形金属盒半径为R,两盒间狭缝的间距为d,磁感应强度为B的匀强磁场与盒面垂直,被加速粒子的质量为m,电荷量为+q,加在狭缝间的交变电压如题15-2图所示,电压值的大小为Ub。周期T= 。一束该粒子在t=0- 时间内从A处均匀地飘入狭缝,其初速度视为零。现考虑粒子在狭缝中的运动时间,假设能够出射的粒子每次经过狭缝均做加速运动,不考虑粒子间的相互作用。求:

①出折粒子的动能 ;②粒子从飘入狭缝至动能达到 所需的总时间
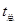 ;
;③要使飘入狭缝的粒子中有超过99%能射出,d应满足的条件.
9.质量为m、电荷量为q的带负电粒子自静止开始释放,经M、N板间的电场加速后,从A点垂直于磁场边界射入宽度为d的匀强磁场中,该粒子离开磁场时的位置P偏离入射方向的距离为L , 如图所示.已知M、N两板间的电压为U , 粒子的重力不计.求:匀强磁场的磁感应强度B.
 10.
10.如图所示,套在很长的绝缘直棒上的带正电的小球,其质量为m , 带电荷量为+q , 小球可在棒上滑动,现将此棒竖直放在互相垂直的匀强电场和匀强磁场中,电场强度为E , 磁感应强度为B , 小球与棒的动摩擦因数为μ , 求小球由静止沿棒下滑的最大加速度和最大速度(设小球电荷量不变)。
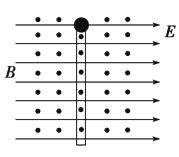 11.
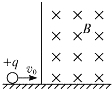
11.如图所示,一个质量为m , 电荷量为q的带正电的小球以速度v0沿水平光滑绝缘平面向右运动.在运动的正前方向有一垂直于纸面向里的匀强磁场,磁感应强度的大小为B , 磁场左边有边界,右边无边界.当小球在磁场中离开平面向上升高h时,速度方向变为竖直向上,求此时小球所受洛伦兹力的大小和方向.(重力加速度为g)
 12.
12.如图,A、C两点分别位于x轴和y轴上,∠OCA=30°,OA的长度为L。在△OCA区域内有垂直于xOy平面向里的匀强磁场。质量为m、电荷量为q的带正电粒子,以平行于y轴的方向从OA边射入磁场。已知粒子从某点射入时,恰好垂直于OC边射出磁场,且粒子在磁场中运动的时间为t0。不计重力。

①求磁场的磁感应强度的大小;
②若粒子先后从两不同点以相同的速度射入磁场,恰好从OC边上的同一点射出磁场,求该粒子这两次在磁场中运动的时间之和;
③若粒子从某点射入磁场后,其运动轨迹与AC边相切,且在磁场内运动的时间为 ,求粒子此次入射速度的大小。
13. 长为 的平行金属板水平放置,两极板带等量的异种电荷,板间形成匀强电场,一个带电荷量为+ 、质量为 的带电粒子,以初速度 紧贴上极板垂直于电场线方向进入该电场,刚好从下极板边缘射出,射出时末速度与下极板成 的角,如图所示,不计粒子重力,求:
匀强电场的场强;两板间的距离.
14. 如图所示,电子由静止开始经加速电场加速后,沿平行于板面的方向射入偏转电场,并从另一侧射出。已知电子质量为m,电荷量为e,加速电场电压为U0。偏转电场可看做匀强电场,极板间电压为U,极板长度为L,板间距为d。忽略电子所受重力,求电子射入偏转电场时的初速度v0和从电场射出时沿垂直板面方向的偏转距离Δy. 15. 如图,两金属板P、Q水平放置,间距为d。两金属板正中间有一水平放置的金属网G,PQG的尺寸相同。G接地,PQ的电势均为 ( >0)。质量为m,电荷量为q(q>0)的粒子自G的左端上方距离G为h的位置,以速度v0平行于纸面水平射入电场,重力忽略不计。
15. 如图,两金属板P、Q水平放置,间距为d。两金属板正中间有一水平放置的金属网G,PQG的尺寸相同。G接地,PQ的电势均为 ( >0)。质量为m,电荷量为q(q>0)的粒子自G的左端上方距离G为h的位置,以速度v0平行于纸面水平射入电场,重力忽略不计。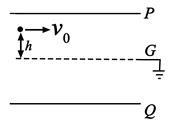 (1)、求粒子第一次穿过G时的动能,以及她从射入电场至此时在水平方向上的位移大小;(2)、若粒子恰好从G的下方距离G也为h的位置离开电场,则金属板的长度最短应为多少?16. 如图,在第一象限存在匀强磁场,磁感应强度方向垂直于纸面(xy平面)向外;在第四象限存在匀强电场,方向沿x轴负向。在y轴正半轴上某点以与x轴正向平行、大小为v0的速度发射出一带正电荷的粒子,该粒子在(d,0)点沿垂直于x轴的方向进入电场。不计重力。若该粒子离开电场时速度方向与y轴负方向的夹角为θ,求:
(1)、求粒子第一次穿过G时的动能,以及她从射入电场至此时在水平方向上的位移大小;(2)、若粒子恰好从G的下方距离G也为h的位置离开电场,则金属板的长度最短应为多少?16. 如图,在第一象限存在匀强磁场,磁感应强度方向垂直于纸面(xy平面)向外;在第四象限存在匀强电场,方向沿x轴负向。在y轴正半轴上某点以与x轴正向平行、大小为v0的速度发射出一带正电荷的粒子,该粒子在(d,0)点沿垂直于x轴的方向进入电场。不计重力。若该粒子离开电场时速度方向与y轴负方向的夹角为θ,求: (1)、电场强度大小和磁感应强度大小的比值;(2)、该粒子在电场和磁场中运动的总时间。
(1)、电场强度大小和磁感应强度大小的比值;(2)、该粒子在电场和磁场中运动的总时间。