苏科版初中数学七年级下册 12.2 证明 同步训练(基础版)
试卷更新日期:2022-03-23 类型:同步测试
一、单选题
-
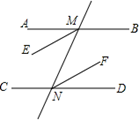
1. 用反证法证明命题:“如图,如果AB//CD,AB//EF,那么CD//EF.”证明的第一个步骤是( )
 A、假定CD//EF B、假定CD不平行于EF C、已知AB//EF D、假定AB不平行于EF2. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.
A、假定CD//EF B、假定CD不平行于EF C、已知AB//EF D、假定AB不平行于EF2. 定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD是△ABC的外角.求证:∠ACD=∠A+∠B.证法1:如图,
∵∠A=70°,∠B=63°,
且∠ACD=133°(量角器测量所得)
又∵133°=70°+63°(计算所得)
∴∠ACD=∠A+∠B(等量代换).
证法2:如图,
∵∠A+∠B+∠ACB=180°(三角形内角和定理),
又∵∠ACD+∠ACB=180°(平角定义),
∴∠ACD+∠ACB=∠A+∠B+∠ACB(等量代换).
∴∠ACD=∠A+∠B(等式性质).
下列说法正确的是( )
 A、证法1用特殊到一般法证明了该定理 B、证法1只要测量够100个三角形进行验证,就能证明该定理 C、证法2还需证明其他形状的三角形,该定理的证明才完整 D、证法2用严谨的推理证明了该定理3. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、
A、证法1用特殊到一般法证明了该定理 B、证法1只要测量够100个三角形进行验证,就能证明该定理 C、证法2还需证明其他形状的三角形,该定理的证明才完整 D、证法2用严谨的推理证明了该定理3. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、 B、
B、 C、
C、 D、
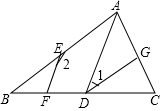
D、 4. 如图,给出下列条件:① ;② ;③ ,且 ;④ 且 ;其中能推出 的条件为( )
4. 如图,给出下列条件:① ;② ;③ ,且 ;④ 且 ;其中能推出 的条件为( ) A、①② B、②④ C、②③ D、②③④5. 阅读下列材料,其①~④步中数学依据错误的是( )
A、①② B、②④ C、②③ D、②③④5. 阅读下列材料,其①~④步中数学依据错误的是( )如图:已知直线 , ,求证: .
证明:①∵ (已知)
∴ (垂直的定义)
②又∵ (已知)
③∴ (同位角相等,两直线平行)
∴ (等量代换)
④∴ (垂直的定义).
A、① B、② C、③ D、④6. 如图,点E在BA的延长线上,能证明BE∥CD是( ) A、∠EAD=∠B B、∠BAD=∠BCD C、∠EAD=∠ADC D、∠BCD+∠D=180°7. 如图,下列条件中能证明AD BC的是( )
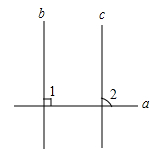
A、∠EAD=∠B B、∠BAD=∠BCD C、∠EAD=∠ADC D、∠BCD+∠D=180°7. 如图,下列条件中能证明AD BC的是( )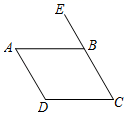 A、∠A=∠C B、∠ABE=∠C C、∠A+∠D=180° D、∠C+∠D=180°8. 已知a,b,c是三条直线,下列结论正确的是( )A、若a∥b,b∥c,则a∥c B、若a⊥b,b⊥c,则a⊥c C、若a∥b,b⊥c,则a∥c D、若a⊥b,b∥c,则a∥c9. 如图,下列推理及所证明的理由都正确的是( )
A、∠A=∠C B、∠ABE=∠C C、∠A+∠D=180° D、∠C+∠D=180°8. 已知a,b,c是三条直线,下列结论正确的是( )A、若a∥b,b∥c,则a∥c B、若a⊥b,b⊥c,则a⊥c C、若a∥b,b⊥c,则a∥c D、若a⊥b,b∥c,则a∥c9. 如图,下列推理及所证明的理由都正确的是( )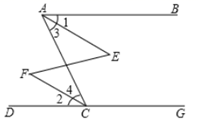 A、若 ,则 ,理由是内错角相等,两直线平行 B、若 ,则 ,理由是两直线平行,内错角相等 C、若 ,则 ,理由是内错角相等,两直线平行 D、若 ,则 ,理由是两直线平行,内错角相等10. 下列选项中,可以用来证明命题“若a2-4a=0,则a=0”是假命题的反例是( ).A、a = -2 B、a = -1 C、a = 4 D、a = 2
A、若 ,则 ,理由是内错角相等,两直线平行 B、若 ,则 ,理由是两直线平行,内错角相等 C、若 ,则 ,理由是内错角相等,两直线平行 D、若 ,则 ,理由是两直线平行,内错角相等10. 下列选项中,可以用来证明命题“若a2-4a=0,则a=0”是假命题的反例是( ).A、a = -2 B、a = -1 C、a = 4 D、a = 2二、填空题
-
11. 命题“若x(1﹣x)=0,则x=0”是命题(填“真”、假),证明时可举出的反例是 .12. 完成下面的证明:已知:如图, .求证: ∥ .
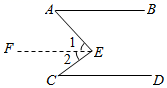
证明:过点 作 ∥ .
▲ ( ).
,
.
▲ ∥ ▲ ( ).
∥ ( ).
13. 取一个自然数,若它是奇数,则乘以3加上1,若它是偶数,则除以2,按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明.但举例验证都是正确的.例如:取自然数5.最少经过下面5步运算可得1,即: ,如果自然数 最少经过7步运算可得到1,则所有符合条件的 的值为 .14. 如图,等边三角形 中, 为 的中点, 平分 ,且交 于 .如果用“三角形三条角平分线必交于一点”来证明 也一定平分 ,那么必须先要证明 . 15. 完成下面的证明:(1)、已知:如图,AB∥CD
15. 完成下面的证明:(1)、已知:如图,AB∥CD求证:∠1+∠3 = 180°

证明:∵ AB∥CD(已知),
∴ ∠1+∠2 = 180°()
又∵ ∠2 = ∠3()
∴ ∠1+∠3=180°()
(2)、已知:如图,AM∥EF , ∠1 = ∠B .求证:∠2 = ∠C .
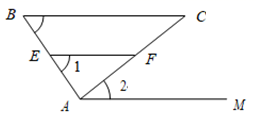
证明:∵ ∠1 = ∠B(已知),
∴ EF∥BC()
∵ AM∥EF(已知),
∴ AM∥BC()
∴ ∠2 = ∠C()
16. 在数学活动课上,老师说有人根据如下的证明过程,得到“1=2”的结论.设a、b为正数,且a=b.
∵a=b,
∴ab=b2 . ①
∴ab﹣a2=b2﹣a2 . ②
∴a(b﹣a)=(b+a)(b﹣a). ③
∴a=b+a. ④
∴a=2a. ⑤
∴1=2. ⑥
大家经过认真讨论,发现上述证明过程中从某一步开始出现不正确,这一步是(填入编号),造成不正确原因是 .
三、解答题
-
17. 如图所示,∠B=∠C,AB∥CD,证明:CE∥BF.
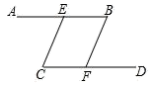 18. 已知:如图, , .
18. 已知:如图, , .求证: ∥ .
 19. 如图, ,点 为直线 , 的交点, .
19. 如图, ,点 为直线 , 的交点, .求证: .
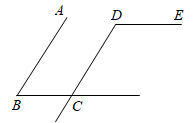 20. 如图,已知 平分 交 于点E, .
20. 如图,已知 平分 交 于点E, .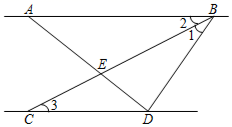 (1)、证明:(2)、若 于点D, ,求 的度数.21. 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2.
(1)、证明:(2)、若 于点D, ,求 的度数.21. 已知:如图,CD⊥AB,FG⊥AB,垂足分别为D、G,点E在AC上,且∠1=∠2.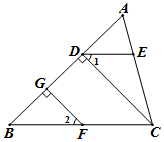 (1)、求证:DE BC;(2)、如果∠B=46°,且∠A比∠ACB小10°,求∠DEC的度数.22. 如图,已知直线AB∥CD , 直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF
(1)、求证:DE BC;(2)、如果∠B=46°,且∠A比∠ACB小10°,求∠DEC的度数.22. 如图,已知直线AB∥CD , 直线MN分别交AB、CD于M、N两点,若ME、NF分别是∠AMN、∠DNM的角平分线,试说明:ME∥NF解:∵AB∥CD , ( ▲ )
∴∠AMN=∠DNM( ▲)
∵ME、NF分别是∠AMN、∠DNM的角平分线,(已知)
∴∠EMN= ▲∠AMN ,
∠FNM= ▲∠DNM (角平分线的定义)
∴∠EMN=∠FNM(等量代换)
∴ME∥NF( ▲)
由此我们可以得出一个结论:两条平行线被第三条直线所截,一对 ▲角的平分线互相 ▲ .