苏科版初中数学七年级下册11.6 一元一次不等式组 同步训练(基础版)
试卷更新日期:2022-03-23 类型:同步测试
一、单选题
-
1. 不等式组 的解在数轴上表示为( )A、
 B、
B、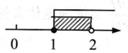 C、
C、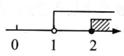 D、
D、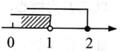 2. 不等式组 的解等于( ).A、1<x<2 B、x>1 C、x<2 D、x<1或x>23. 若不等式组 的解集是x>3,则m的取值范围是( )A、m>3 B、m≥3 C、m≤3 D、m<34. 若不等式组 无解,则 取值范围是( )A、 B、 C、 D、5. 已知 ,且 ,则k的取值范围为( )A、 B、 C、 D、6. 若关于 的不等式组 的解集为 ,则 的值为( )A、-6 B、6 C、-8 D、87. 已知关于 , 的不等式组: 有以下说法:①若它的解集是 ,则 ;②当 时,它无解;③若它的整数解只有2,3,4,则 ;④若它有解,则 .其中所有正确说法的序号是( ).A、①②③ B、①②④ C、④ D、②④8. 已知关于x、y的二元一次方程组 的解满足 ,且关于x的不等式组 有解,那么所有符合条件的整数a的个数为( )A、6个 B、7个 C、8个 D、9个9. 若关于x的不等式组 的整数解只有2个,则m的取值范围是( )A、 B、 C、 D、10. 定义:对于实数 ,符号 表示不大于 的最大整数.例如:[3.2]=3,[2]=2,[-2.3]=-3.如果 ,则 的取值范围是( )A、 B、 C、 D、
2. 不等式组 的解等于( ).A、1<x<2 B、x>1 C、x<2 D、x<1或x>23. 若不等式组 的解集是x>3,则m的取值范围是( )A、m>3 B、m≥3 C、m≤3 D、m<34. 若不等式组 无解,则 取值范围是( )A、 B、 C、 D、5. 已知 ,且 ,则k的取值范围为( )A、 B、 C、 D、6. 若关于 的不等式组 的解集为 ,则 的值为( )A、-6 B、6 C、-8 D、87. 已知关于 , 的不等式组: 有以下说法:①若它的解集是 ,则 ;②当 时,它无解;③若它的整数解只有2,3,4,则 ;④若它有解,则 .其中所有正确说法的序号是( ).A、①②③ B、①②④ C、④ D、②④8. 已知关于x、y的二元一次方程组 的解满足 ,且关于x的不等式组 有解,那么所有符合条件的整数a的个数为( )A、6个 B、7个 C、8个 D、9个9. 若关于x的不等式组 的整数解只有2个,则m的取值范围是( )A、 B、 C、 D、10. 定义:对于实数 ,符号 表示不大于 的最大整数.例如:[3.2]=3,[2]=2,[-2.3]=-3.如果 ,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 在某种药品的说明书上的部分内容是“用法用量:每天 ,分2~3次服用”.则一次服用这种药品的剂量 的范围是 .12. 对于任意有理数 、 ,定义一种运算: .例如, .根据上述定义可知:不等式 的最大整数解是.13. 不等式组 的整数解为 .14. 关于x的不等式组 的解集为﹣1<x<2,则a+b的值为 .15. 现有一条长度为359mm的铜管料,把它锯成长度分别为39mm和29mm的两种不同规格的小铜管,(要求没有余料).每锯一次损耗1mm的铜管料.为了使铜管料损耗最少,应分别锯成39mm的小铜管段,29mm的小铜管段.16. 如果关于 的不等式组 的最大整数解与最小整数解的差为 ,则实数 的取值范围是.17. 若不等式组 无解,化简 得 .18. 若关于x的一元一次不等式组 仅有2个整数解,则m的取值范围是.
三、解答题
-
19. 解不等式组(1)、(2)、20. 解不等式组 ,把解集在数轴上表示出来,并写出不等式组的所有整数解。21. 若关于x , y的方程组 的解,使不等式组 成立,求 的取值范围.22. 阅读理解题
先阅读理解下面的问题,再按要求完成下列问题
例:解不等式
解:由有理数的乘法法则“两数相乘,同号得正”有① 或②
解不等式组①,得
解不等式组②,得
所以不等式 的解集为 或
解不等式:
23. 已知关于x,y的二元一次方程组(1)、若方程组的解 x,y的值互为相反数,求k的值;(2)、若方程组的解x,y的值满足x<1,且 ,求k的取值范围.24. 已知关于x,y的方程组 (m是常数).(1)、若此方程组的解满足x≥0,y>0,求m的取值范围;(2)、在(1)的条件下,化简:|m+2|+|m﹣3|.25. 已知关于 , 的方程组(1)、求方程组的解(用含 的式子表示);(2)、若方程组的解满足不等式组 求满足条件的 的取值范围.26. 如图按下列程序进行计算.规定:程序运行到“判断结果是否大于244”为一次运算,结果大于244,则输出此结果;若结果不大于244,则将此结果的值赋给m , 再进行第二次计算. (1)、当m=100时,求输出的结果是多少?(2)、若m=5,求运算进行多少次才会停止?(3)、若运算进行了5次才停止.求m的取值范围.27. 对非负数x“四舍五入”到个位的值记为〈x〉,即当n为非负整数时,若n﹣0.5≤x<n+0.5,则〈x〉=n.反之,当n为非负整数时,若〈x〉=n,则n﹣0.5≤x<n+0.5.如〈1.34〉=1,〈4.86〉=5.(1)、〈π〉=;(2)、若〈0.5x﹣1〉=7,则实数x的取值范围是 ;(3)、若关于x的不等式组 的整数解恰有4个,求a的取值范围;(4)、满足〈x〉= x的所有非负数x的值为 .28. 今年6月初,由于持续暴雨,某市遭受严重水涝灾害,群众失去家园,市民政局为解决灾民困难,紧急组织了一批救灾帐篷和食品准备送往灾区.已知这批物质中,帐篷和食品共320件,且帐篷比食品多80件.(1)、求帐篷和食品各有多少件?(2)、现计划租用 两种货车共8辆,一次性将这批物质全部送到灾民手中,已知两种货车可装帐篷和食品的件数以及每辆货车所需付运费情况如下表,求出运费最少的方案?最少运费是多少?
(1)、当m=100时,求输出的结果是多少?(2)、若m=5,求运算进行多少次才会停止?(3)、若运算进行了5次才停止.求m的取值范围.27. 对非负数x“四舍五入”到个位的值记为〈x〉,即当n为非负整数时,若n﹣0.5≤x<n+0.5,则〈x〉=n.反之,当n为非负整数时,若〈x〉=n,则n﹣0.5≤x<n+0.5.如〈1.34〉=1,〈4.86〉=5.(1)、〈π〉=;(2)、若〈0.5x﹣1〉=7,则实数x的取值范围是 ;(3)、若关于x的不等式组 的整数解恰有4个,求a的取值范围;(4)、满足〈x〉= x的所有非负数x的值为 .28. 今年6月初,由于持续暴雨,某市遭受严重水涝灾害,群众失去家园,市民政局为解决灾民困难,紧急组织了一批救灾帐篷和食品准备送往灾区.已知这批物质中,帐篷和食品共320件,且帐篷比食品多80件.(1)、求帐篷和食品各有多少件?(2)、现计划租用 两种货车共8辆,一次性将这批物质全部送到灾民手中,已知两种货车可装帐篷和食品的件数以及每辆货车所需付运费情况如下表,求出运费最少的方案?最少运费是多少?帐篷(件)
食品(件)
每辆需付运费(元)
种货车
40
10
780
种货车
20
20
700