2022年高考物理三轮冲刺练习专题四动量和能量

试卷更新日期：2022-03-23 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 如图，在光滑水平面上，轨道ABCD的质量M =0.4 kg，其中AB段是半径R=0.4 m的光滑 $\frac{1}{4}$ 弧，在B点与水平轨道BD相切，水平轨道的BC段粗糙，动摩擦因数μ=0.4，长L=3.5 m，C点右侧的轨道光滑，轨道的右端连接一轻质弹簧。现有一质量m=0.1kg的小物体在A点正上方高为H=3.6m处由静止自由落下，恰沿A点切线滑入圆弧轨道，重力加速度g=10 m/s²。下列说法正确的是（）

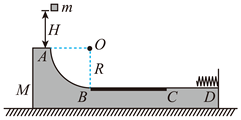A、小物体和轨道组成的系统在全过程中动量守恒 B、小物体第一次返回到A点时的速度为 $2 \sqrt{6}$ m/s C、小物体第一次返回到A点时的速度为0 D、轨道M在水平面上运动的最大速率为2.0 m/s.

查看试题解析

二、多选题

2. 如图所示，一质量为m、半径为R的四分之一光滑圆弧槽，放在光滑的水平面上，有一质量也为m的小球由槽顶端A静止释放，在其下滑至槽末端B的过程中，已知重力加速度为g，空气阻力忽略不计。则下列说法正确的是（）

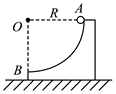A、若圆弧槽固定，小球的机械能守恒 B、若圆弧槽固定，小球滑至B点时对槽的压力大小为4mg C、若圆弧槽不固定，小球和槽组成的系统动量守恒 D、圆弧槽固定和不固定情形下，小球滑到B点时的速度之比为 $\sqrt{2} ： 1$

查看试题解析
3. 如图所示，质量为M的木板静止在光滑水平面上，木板左端固定一轻质挡板，一根轻弹簧左端固定在挡板上，质量为m的小物块从木板最右端以速度v₀滑上木板，压缩弹簧，然后被弹回，运动到木板最右端时与木板相对静止。已知物块与木板之间的动摩擦因数为μ，整个过程中弹簧的形变均在弹性限度内，则（）

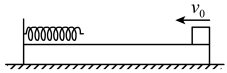A、运动过程中m、M和弹簧组成的系统机械能守恒 B、整个过程中合力对物块的冲量大小为 $\frac{M m v_{0}}{M + m}$ C、m在M上相对运动的路程为 $\frac{m v_{0}^{2}}{2 μ g (m + M)}$ D、整个过程弹簧弹性势能的最大值为 $\frac{M m v_{0}^{2}}{4 (m + M)}$

查看试题解析
4. 如图所示，在光滑水平面的左侧固定一竖直弹性挡板，挡板右侧依次放有10个质量均为2m的弹性白色小球（在一条直线上），一质量为m的红色小球以与白色小球共线的速度v₀与1号小球发生弹性正碰，红色小球反弹后与挡板弹性碰撞，碰后速度方向与碰前速度相反，两弹性白色小球碰撞时交换速度，则下列说法中正确的是（）

A、10号小球最终速度v₀ B、10号小球最终速度 $\frac{2}{3} v_{0}$ C、红色小球最终速度 ${(\frac{2}{3})}^{10} v_{0}$ D、红色小球最终速度 ${(\frac{1}{3})}^{10} v_{0}$

查看试题解析
5. 如图所示，两足够长的光滑平行金属导轨MN、PQ水平放置，导轨间距为L，虛线OO'垂直导轨，OO'两侧导轨所在空间区域存在着磁感应强度大小均为B的方向相反的竖直匀强磁场，两长度均为L、电阻均为R、质量均为m的金属导体棒a、b垂直导轨放在OO'左右两侧，并与导轨保持良好接触，不计其它电阻。现给导体棒a一个瞬时冲量，使a获得一个水平向右的初速度 $v_{0}$ ，下列关于a、b两棒此后整个运动过程的说法正确的是（）

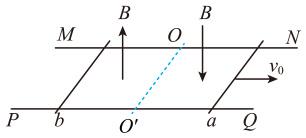A、a、b两棒组成的系统动量守恒 B、a、b两棒最终都将以大小为 $\frac{v_{0}}{2}$ 的速度做匀速直线运动 C、整个过程中，流过a棒的电荷量为 $\frac{m v_{0}}{2 B L}$ D、整个过程中，a棒上产生的焦耳热为 $\frac{1}{4} m v_{0}^{2}$

查看试题解析
6. 图甲所示，质量分别为 $m_{A}$ 和 $m_{B}$ 的两物体用轻弹簧连接置于光滑水平面，初始时两物体被锁定，弹簧处于压缩状态。 $t = 0$ 时刻将B物体解除锁定， $t = t_{1}$ 时刻解除A物体的锁定，此时B物体的速度为 $v_{0}$ ， AB两物体运动的 $a - t$ 图像如图乙所示，其中 $S_{1}$ 和 $S_{2}$ 分别表示 $0 ∼ t_{1}$ 时间和 $t_{1} ∼ t_{3}$ 时间内B物体的 $a - t$ 图像与坐标轴所围面积的大小，则下列说法正确的是（）

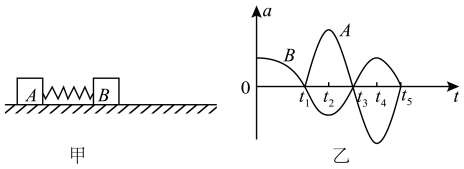A、 $m_{A} < m_{B}$ B、 $S_{1} > S_{2}$ C、 $t_{4}$ 时刻，弹簧伸长量最大 D、 $0 ∼ t_{5}$ 时间内，弹簧对A物体的冲量大小为 $m_{B} v_{0}$

查看试题解析
7. 如图所示，两辆小车能在光滑的水平面上自由移动，甲车质量为1kg，乙车质量为2kg，甲车前方固定一根轻质弹簧。推动一下使两车相向而行，若某时刻甲的速度为3m/s，乙的速度为2m/s，弹簧始终在弹性范围内作用，则（）

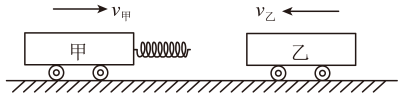A、甲车开始反向时，乙车速度减为0.5m/s，方向不变 B、乙车开始反向时，甲车速度减为0.5m/s，方向与原来的速度方向一致 C、相互作用时弹簧弹性势能最大为8.5J D、两车距离最近时，速度相等，方向都与乙车原来的速度方向一致

查看试题解析

三、综合题

8. 如图所示，在距水平地面高h=0.80m的水平桌面左边缘有一质量m_A=1.0kg的物块A以v₀=5.0m/s的初速度沿桌面运动，经过位移s=1.8m与放在桌面右边缘O点的物块B发生完全非弹性碰撞，碰后物块B离开桌面后落到地面上的位置到桌边缘O点的水平距离为1.0m.设两物块均可视为质点，它们的碰撞时间极短，物块A与桌面间的动摩擦因数μ=0.25，重力加速度g=10m/s²。求：

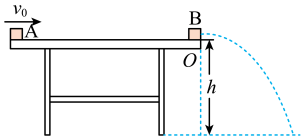(1)、两物块碰撞前瞬间，物块A的速度大小v_A；

(2)、物块A与B碰撞后的瞬间，物块B的速度；

(3)、物块A与B碰撞的过程中系统损失的机械能E 。

查看试题解析
9. 如图所示，倾角 $θ = 30 °$ 的光滑斜面体固定在水平面上，斜面底端固定一挡板D，自由长度为L₀的轻弹簧一端固定在D上，质量为m的小物块B与弹簧连接，另一相同的小物块C从斜面上端与挡板D相距1.9L₀处的P点由静止释放，C与B碰撞后粘合在一起（碰撞时间极短）。已知重力加速度大小为g，弹簧的劲度系数为 $k = \frac{5 m g}{L_{0}}$ ，弹簧的形变量为x时具有的弹性势能为 $\frac{1}{2} k x^{2}$ 。求：

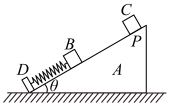(1)、开始时弹簧的形变量x；

(2)、C与B碰后粘合体的速度v；

(3)、碰后粘合体的最大动能Ek。

查看试题解析
10. 如图所示，质量为 $M$ 的木块静止在光滑的水平面上，一质量为 $m$ 、速度为 $v_{0}$ 的子弹水平射入木块且未穿出.设木块对子弹的阻力恒为 $F$ ，问：

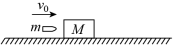(1)、射入过程中产生的内能为多少?

(2)、木块至少为多长时子弹才不会穿出?

(3)、子弹在木块中运动了多长时间?

查看试题解析
11. 如图所示，质量为 $m_{1} = 0.2 k g$ ，电阻为 $r_{1} = 0.5 Ω$ 的均匀金属棒 $a b$ 垂直架在水平面内间距为 $L = 1 m$ 的两光滑金属导轨的右边缘处。下方的光滑绝缘圆弧轨道与光滑水平金属导轨相切，圆弧轨道半径为 $R = 0.1 m$ 、对应圆心角为 $60 °$ 、水平金属导轨间距为 $L = 1 m$ ， $M N_{1} = P N_{2} = 0.4 m$ 。 $c d e f$ 是质量 $m_{2} = 0.2 k g$ 、电阻 $r_{2} = 1.5 Ω$ 、各边长度均为 $L = 1 m$ 的“U”形金属框，金属框上c、f两点与导轨 $N_{1}$ 、 $N_{2}$ 两点接触良好，所有导轨的电阻都不计。以 $N_{2}$ 点为坐标原点，沿水平向右方向建立x坐标轴，整个空间存在竖直方向的磁场（未画出），磁感应强度分布规律为 $B = {\begin{array}{l} - 1 T ， x < 0 \\ (1 + 0.8 x) T ， x \geq 0 \end{array}$ （取竖直向上为正方向）。闭合开关S，金属棒 $a b$ 水平抛出，下落高度 $h = \frac{9}{80} m$ 时，恰好沿圆弧轨道上端的切线落入，接着沿圆弧轨道下滑进入 $M N_{1} P N_{2}$ 水平导轨；起始时刻 $c d e f$ 金属框固定，当叻 $a b$ 棒与其碰前瞬间解除固定，且两者碰撞粘连后形成闭合金属框 $c d e f$ ， $a b$ 棒与导轨始终接触良好， $N_{1} N_{2}$ 右侧水平面光滑绝缘。重力加速度 $g = 10 m / s^{2}$ 。

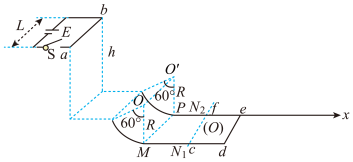(1)、求 $a b$ 棒从闭合开关S到水平抛出的过程中产生的冲量；

(2)、求 $a b$ 棒与金属框 $c d e f$ 碰撞后瞬间的速度大小；

(3)、求闭合金属框 $c d e f$ 最终静止时 $e d$ 边的位置坐标。

查看试题解析
12. 如图所示，长为 $l_{0} = 1 m$ 粗糙水平轨道的左端连接倾角为 $θ = 3 7^{°}$ 的粗糙斜面，右端平滑连接着半径均为 $R = 0.1 m$ 的四分之一光滑圆弧轨道BC和四分之一光滑细圆轨道CD，长为 $l = 1 m$ ，质量为 $M = 2 k g$ 的长木板置于斜面上，开始时长木板的底端与斜面的底端对齐且与AB齐平（不考虑物体经该处的能量损失）.一质量为 $m_{1} = 1 k g$ 的小物块1（可看成质点）从长木板顶端由静止开始下滑.已知小物块和木板间动摩擦因数为 $μ_{1} = \frac{1}{8}$ ，小物块和水平轨道间动摩擦因数为 $μ_{2} = \frac{3}{4}$ ，长木板和斜面间动摩擦因数为 $μ_{3} = \frac{7}{24}$ ，取 $g = 10 m / s^{2}$

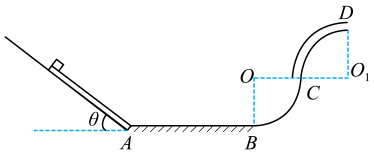(1)、求小物块1停下后距A点的距离x；

(2)、现将长木板置于底端距A点为 $l = 1.5 m$ 处，小物块1仍从长木板的顶端随长木板一起静止释放，求在D点处轨道对小物块1的作用力 $N_{D}$ ；

(3)、将水平粗糙轨道换成光滑轨道，再次将长木板置于底端距A点一定距离，小物块1仍从长木板的顶端随长木板一起静止释放，释放前在A点处放另一质量为 $m_{2} = 1 k g$ 的小物块2，小物块1运动到A点处与小物块2碰撞后粘在一起，之后小物块12刚好过D点，求整个过程中由于摩擦所产生的热量Q（不考虑小物块12再次滑回轨道）。

查看试题解析
13. 如图所示，有一倾角为α＝30°的光滑斜面固定在水平面上，质量为m_A＝1kg的滑块A(可以看做质点)在水平向左的恒力F作用下静止在距离斜面底端x＝5m的位置上，水平面上有一质量为m_B＝1kg的表面光滑且足够长的木板B，B的右端固定一轻质弹簧，一质量为m_C＝3kg的物块C与弹簧的左端拴接。开始时，B、C静止且弹簧处于原长状态，今将水平力F变为水平向右，当滑块A刚好滑到斜面底端时撤去力F，不考虑A滑上水平面过程的能量损失。滑块A运动到水平面上后与滑块B发生对心碰撞(碰撞时间极短)粘在一起，并拉伸弹簧使滑块C向前运动，不计一切摩擦，g取10m/s² ，求：

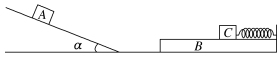(1)、水平力F的大小及滑块A滑到斜面底端时的速度v_A；

(2)、被拉伸弹簧的最大弹性势能E_p及滑块C的最大速度v_C。

查看试题解析
14. 如图所示，水平地面光滑，四分之一表面光滑的圆弧形轨道P固定在地面上，半径为R，紧挨着轨道p的右端是表面粗糙的长木板Q，二者水平部分等高，Q的质量为2m。开始时木板Q通过一装置锁定在地面上，质量为2m的小滑块B静止于距Q的左端3R处。现有质量为m的小滑块A从P顶端静止释放，已知A、B与Q之间的动摩擦因数均为 $μ = \frac{1}{6}$ ， A、B可看成质点，重力加速度为g。

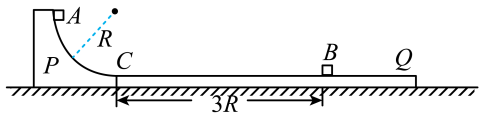(1)、求小滑块A滑到圆弧形轨道的最低点C时轨道所受的压力多大？

(2)、A、B相碰为完全非弹性碰撞，A与B碰撞瞬间木板Q解除锁定，要使物块不滑离长木板，求长木板Q的长度至少多大？

查看试题解析
15. 如图所示，MPQ、M′P′Q′是光滑平行导轨，其中倾斜部分MPP′M′为金属材料制成，电阻可不计，倾角为α=37°，并处在与MPP′M′平面垂直且向下的匀强磁场中（图中未画出），磁感应强度大小为2T；水平部分PQQ′P′为绝缘材料制成，所在空间内存在竖直方向的磁场，在PQ上取一点为坐标原点O，沿PQ方向建立x轴，可知磁感应强度分布规律为 $B = {\begin{array}{l} - 0.125 T \begin{array}{l} x < 0 \end{array} \\ (0.125 + 2 x) T \begin{array}{l} x \geq 0 \end{array} \end{array}$ （取竖直向上为正方向）；两部分导轨的衔接处用小圆弧连接，金属棒通过时无机械能损失，两导轨间接有阻值为R=5Ω的定值电阻。正方形金属线框cdef的质量m₂=2kg、边长为L=1m，每条边的电阻r₂=2Ω，f点刚好位于坐标原点，fc边与PP′平行。现将一根质量m₁=1kg，长度L=1m，电阻r₁=2Ω的金属棒ab从图示位置静止释放，滑到斜面底端前已达到匀速运动。若整个过程ab棒、金属框与导轨始终接触良好，（重力加速度g=10m/s² ， $s i n 37 ° = 0.6$ ， $c o s 37 ° = 0.8$ ），求：

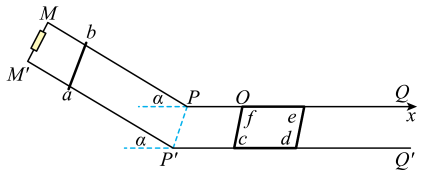(1)、ab棒滑到底端时的速度大小和ab棒两端的电压U_ab；

(2)、ab棒与金属线框碰撞后合成一个整体一起在轨道上滑行，滑行过程中ed边产生的焦耳热；

(3)、第（2）所涉及的滑行过程中，通过ed棒的电荷量。

查看试题解析
16. 如图甲所示，以 $v = 1.8 m / s$ 的速度顺时针匀速转动的传送带与水平面夹角 $θ = 37 °$ ，质量为3kg的小物块B与物块C间拴接一轻弹簧，B、C同时静止释放，且此时弹簧恰好处于原长，B、C与斜面间的动摩擦因数均为0.75。质量为1kg的小物块A在与物块B距离0.6m处，以 $v_{0} = 6 m / s$ 的初速度沿斜面向下运动，A与斜面间动摩擦因数也为0.75，传送带的上、下端均足够长，A、B碰撞无机械能损失。以A、B碰撞的时刻为0时刻，B、C物块运动的 $a - t$ 图像如图乙所示，规定沿斜面向下为正方向，其中，第四象限图线在0到 $t_{0}$ 时间内与坐标轴围成的面积大小为 $S_{1}$ ，第一象限图线在0到 $2 t_{0}$ 时间内与坐标轴围成的面积大小为 $S_{2}$ ，重力加速度 $g = 10 m / s^{2}$ 。求：

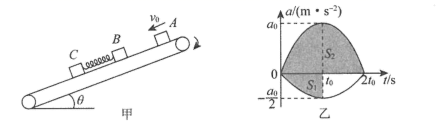(1)、物块A从开始运动到再回到释放高度所用的时间t（A、B碰撞时间忽略不计）；

(2)、物块C的质量 $m_{C}$ 及图线与坐标轴围成的面积 $S_{1}$ 、 $S_{2}$ 的大小；

(3)、若0到 $2 t_{0}$ 时间内C的位移 $x_{0} = 0.2 m$ ，则这一过程中B、C和弹簧组成的系统机械能变化了多少。

查看试题解析
17. 如图，在竖直平面内，一半径为 $R = 1 m$ 的光滑圆弧绝缘轨道 $A B C$ 和光滑水平绝缘轨道 $O A$ 在A点相切， $A B$ 为直径， $O$ 为圆心， $O' B$ 和 $O' C$ 之间的夹角为α， $s i n α = \frac{3}{5}$ 。在I象限（含x、y轴）有水平向右的匀强电场 $E_{1}$ ，在II象限（不含y轴）有竖直向上的匀强电场 $E_{2}$ 和垂直于纸面向里的矩形区域的匀强磁场B（未画出）。有一质量为m、电量为 $+ q$ 的金属a球由坐标原点O由静止释放，运动到A点与静止在圆弧最低点的质量也为m、不带电的金属b球（穿在圆弧轨道上）发生弹性碰撞（系统无机械能损失）。已知 $E_{1} = \frac{12 m g}{q}$ ，大小相等的a、b球，可视为点电荷，接触后电荷均分，重力加速度g取 $10 m / s^{2}$ ，不计a、b球间的静电力。求：

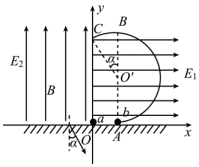(1)、碰撞后，a、b球的速度大小；

(2)、b球到达C点位置时的速度大小；

(3)、若b球离开C位置后，在II象限内做匀速圆周运动，打到x负半轴上时，与竖直方向的夹角为α（如图），求磁场B的大小和矩形区域磁场的最小面积。

查看试题解析

2022年高考物理三轮冲刺练习专题四 动量和能量

一、单选题

二、多选题

三、综合题

2022年高考物理三轮冲刺练习专题四动量和能量