2022年高考物理三轮冲刺练习专题一 直线运动和力
试卷更新日期:2022-03-23 类型:三轮冲刺
一、单选题
-
1. 某质量为m的动车由静止沿平直路线启动,其加速度a与位移x的图像如图所示。已知运动中阻力恒为车重的k倍,重力加速度为g,下列说法不正确的是( )
 A、动车位移为x1时的速度为 B、动车位移为x2时的速度为 C、若 , 在0-x2的过程中,牵引力做功为 D、动车从x1-x2所经历的时间为2. 避险车道是指在长陡下坡路段行车道外侧增设的供速度失控(刹车失灵)车辆驶离正线安全减速的专用车道,如图所示。一辆质量为m的失控载重卡车以速度v冲上避险车道,直线行驶位移x后安全停下。查阅公路设计资料得知,该避险车道的路面与水平路面的夹角为θ。若将载重卡车视为作匀变速直线运动的质点,当地重力加速度为g,关于载重卡车在避险车道上的运动,下列说法正确的是( )
A、动车位移为x1时的速度为 B、动车位移为x2时的速度为 C、若 , 在0-x2的过程中,牵引力做功为 D、动车从x1-x2所经历的时间为2. 避险车道是指在长陡下坡路段行车道外侧增设的供速度失控(刹车失灵)车辆驶离正线安全减速的专用车道,如图所示。一辆质量为m的失控载重卡车以速度v冲上避险车道,直线行驶位移x后安全停下。查阅公路设计资料得知,该避险车道的路面与水平路面的夹角为θ。若将载重卡车视为作匀变速直线运动的质点,当地重力加速度为g,关于载重卡车在避险车道上的运动,下列说法正确的是( ) A、加速度大小为 B、加速度大小为 C、运动时间为 D、损失的机械能为3. 如图所示,物理课上老师做了这样一个实验,将一厚度均匀且足够长的光滑铝板固定在绝缘支架上,铝板与永平面的倾角为 , 现将一质量为m的永磁体静止地放置在铝板的上端,它将沿斜面向下运动,则运动过程中永磁体( )
A、加速度大小为 B、加速度大小为 C、运动时间为 D、损失的机械能为3. 如图所示,物理课上老师做了这样一个实验,将一厚度均匀且足够长的光滑铝板固定在绝缘支架上,铝板与永平面的倾角为 , 现将一质量为m的永磁体静止地放置在铝板的上端,它将沿斜面向下运动,则运动过程中永磁体( ) A、做加速度为a的匀加速直线运动,且 B、做加速度为a的匀加速直线运动,且 C、重力势能先逐渐减小,最后保持不变 D、动能先逐渐增加,最后保持不变4. 一位同学乘坐电梯从六楼下到一楼的过程中,其图象如图所示,下列说法正确的是( )
A、做加速度为a的匀加速直线运动,且 B、做加速度为a的匀加速直线运动,且 C、重力势能先逐渐减小,最后保持不变 D、动能先逐渐增加,最后保持不变4. 一位同学乘坐电梯从六楼下到一楼的过程中,其图象如图所示,下列说法正确的是( ) A、前内该同学处于超重状态 B、前内该同学的加速度是最后内的2倍 C、该同学在内的平均速度是 D、该同学在内通过的位移是5. 如图所示,M、N为水平地面上的两点,在M点上方高处有一个小球A以初速度v0水平抛出,同时,在N点正上方高h处有一个小球B由静止释放,不计空气阻力,结果小球A在与地面第一次碰撞后反弹上升过程中与小球B相碰,小球A与地面相碰前后,水平方向分速度相同,竖直方向分速度大小相等,方向相反,则B球由静止释放到与A球相碰所用的时间为( )
A、前内该同学处于超重状态 B、前内该同学的加速度是最后内的2倍 C、该同学在内的平均速度是 D、该同学在内通过的位移是5. 如图所示,M、N为水平地面上的两点,在M点上方高处有一个小球A以初速度v0水平抛出,同时,在N点正上方高h处有一个小球B由静止释放,不计空气阻力,结果小球A在与地面第一次碰撞后反弹上升过程中与小球B相碰,小球A与地面相碰前后,水平方向分速度相同,竖直方向分速度大小相等,方向相反,则B球由静止释放到与A球相碰所用的时间为( )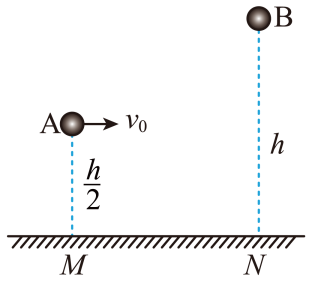 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
6. 如图所示是一质量为50kg的乘客乘电梯上楼过程中图像,g取。下列说法正确的是( )
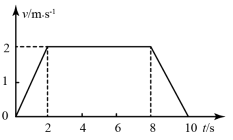 A、时,乘客对电梯底板的压力大小为550N B、0-2s和8-10s两个过程中电梯的加速度相同 C、乘客在8-10s上升过程中处于失重状态,重力消失 D、电梯上升过程的总位移大小为16m,方向竖直向上
A、时,乘客对电梯底板的压力大小为550N B、0-2s和8-10s两个过程中电梯的加速度相同 C、乘客在8-10s上升过程中处于失重状态,重力消失 D、电梯上升过程的总位移大小为16m,方向竖直向上三、综合题
-
7. 如图a所示的“冰爬犁”是北方儿童在冬天的一种游戏用具:“上坐一人,双手握铁篙,向后下方用力点冰,则冰床前进如飞。”在空旷的水平冰面上,有一小孩从静止开始,连续三次“点冰”后,爬犁沿直线继续滑行最后停下。某同学用图像描述了上述运动过程,如图b所示,图中。求:

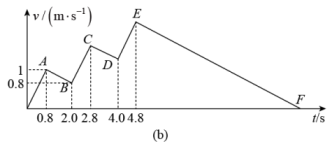 (1)、爬犁加速时的加速度大小;(2)、从O到A过程中的位移大小;(3)、爬犁运动的最大速度为多少?(4)、爬犁运动了多长距离停下?8. 第24届冬季奥运会将于2022年2月在我国举行,冰壶是比赛项目之一。如图,运动员用水平恒力F推着冰壶从起始位置由静止出发,到投掷线时放手,冰壶沿虚线滑行,恰能停在圆垒中心O点。已知恒力 , 冰壶的质量 , 冰壶起始位置到投掷线的距离 , 投掷线到圆垒中心的距离 , 取重力加速度大小。求:
(1)、爬犁加速时的加速度大小;(2)、从O到A过程中的位移大小;(3)、爬犁运动的最大速度为多少?(4)、爬犁运动了多长距离停下?8. 第24届冬季奥运会将于2022年2月在我国举行,冰壶是比赛项目之一。如图,运动员用水平恒力F推着冰壶从起始位置由静止出发,到投掷线时放手,冰壶沿虚线滑行,恰能停在圆垒中心O点。已知恒力 , 冰壶的质量 , 冰壶起始位置到投掷线的距离 , 投掷线到圆垒中心的距离 , 取重力加速度大小。求: (1)、冰壶离手前后的加速度大小之比;(2)、冰壶离手瞬间的速度大小。9. 北京2022年冬奥会冰壶比赛在北京“冰立方”举行,冰壶运动场地如图1所示。M、N为两个完全相同可视为质点的冰壶,M、N与营垒圆心在同一条直线上。一运动员将冰壶M以大小为v0=5m/s的初速度投出使其沿虚线路径向冰壶N撞去,同时运动员会用毛刷擦冰壶M前进方向的冰面,减小冰壶与冰面间的摩擦,擦后动摩擦因数变为原来 , 碰后运动员不再擦冰面,冰壶M、N的图象如图2所示。已知碰撞时间极短,碰后M冰壶恰好停在营垒中心,重力加速度g取。求:
(1)、冰壶离手前后的加速度大小之比;(2)、冰壶离手瞬间的速度大小。9. 北京2022年冬奥会冰壶比赛在北京“冰立方”举行,冰壶运动场地如图1所示。M、N为两个完全相同可视为质点的冰壶,M、N与营垒圆心在同一条直线上。一运动员将冰壶M以大小为v0=5m/s的初速度投出使其沿虚线路径向冰壶N撞去,同时运动员会用毛刷擦冰壶M前进方向的冰面,减小冰壶与冰面间的摩擦,擦后动摩擦因数变为原来 , 碰后运动员不再擦冰面,冰壶M、N的图象如图2所示。已知碰撞时间极短,碰后M冰壶恰好停在营垒中心,重力加速度g取。求: (1)、碰前冰壶N到营垒中心的距离;(2)、冰壶M开始运动时到冰壶N的距离以及冰壶M运动的总时间。10. 如图所示。质的物体从空中某处以沿与水平方向成角斜向上抛出,恰好水平从光滑圆弧轨道最高点处滑入轨道内,且与轨道间无弹力,圆弧轨道与倾角也为角的光滑固定斜面相切于处,距水平面高。斜面在处与光滑水平面平滑相接,质量的物体静止在水平面上,与碰撞后粘为一体从点处冲上足够长的始终顺时针匀速运动的传送带。物体与皮带间的动摩擦因数。 , , 重力加速度取。不计空气阻力,求:
(1)、碰前冰壶N到营垒中心的距离;(2)、冰壶M开始运动时到冰壶N的距离以及冰壶M运动的总时间。10. 如图所示。质的物体从空中某处以沿与水平方向成角斜向上抛出,恰好水平从光滑圆弧轨道最高点处滑入轨道内,且与轨道间无弹力,圆弧轨道与倾角也为角的光滑固定斜面相切于处,距水平面高。斜面在处与光滑水平面平滑相接,质量的物体静止在水平面上,与碰撞后粘为一体从点处冲上足够长的始终顺时针匀速运动的传送带。物体与皮带间的动摩擦因数。 , , 重力加速度取。不计空气阻力,求: (1)、圆弧轨道半径;(2)、物体向左运动距点的最大距离;(3)、若要物体不脱离轨道且不会从处飞出,传送带匀速运动的最大速度。11. 一小物块从全长为5m、倾角为37°的斜面顶端由静止开始沿斜面下滑,其重力势能和动能随下滑距离s的变化如图中直线Ⅰ、Ⅱ所示。(已知sin37°=0.6,cos37°=0.8,g取10m/s2)求:
(1)、圆弧轨道半径;(2)、物体向左运动距点的最大距离;(3)、若要物体不脱离轨道且不会从处飞出,传送带匀速运动的最大速度。11. 一小物块从全长为5m、倾角为37°的斜面顶端由静止开始沿斜面下滑,其重力势能和动能随下滑距离s的变化如图中直线Ⅰ、Ⅱ所示。(已知sin37°=0.6,cos37°=0.8,g取10m/s2)求: (1)、小物块的质量m和下滑过程中的加速度a;(2)、斜面和小物块间的滑动摩擦因数μ;(3)、当小物块的动能与重力势能相等时,沿斜面下滑的时间t。12. 2021年8月11日小米发布了名为Cyber Dog的机器狗。据悉该机器狗拥有多种传感器可实现陪伴、买菜、导盲等功能。小米实验室某次对机器狗的实验过程如下:该机器狗沿着笔直的测试公路从静止开始匀加速前进,经过10s后到达最大速度,这段时间通过的距离16m。保持最大速度匀速前进8s后做匀减速直线运动,经过5s停止运动。已知机器狗(含测试设备)总质量为25kg,求:
(1)、小物块的质量m和下滑过程中的加速度a;(2)、斜面和小物块间的滑动摩擦因数μ;(3)、当小物块的动能与重力势能相等时,沿斜面下滑的时间t。12. 2021年8月11日小米发布了名为Cyber Dog的机器狗。据悉该机器狗拥有多种传感器可实现陪伴、买菜、导盲等功能。小米实验室某次对机器狗的实验过程如下:该机器狗沿着笔直的测试公路从静止开始匀加速前进,经过10s后到达最大速度,这段时间通过的距离16m。保持最大速度匀速前进8s后做匀减速直线运动,经过5s停止运动。已知机器狗(含测试设备)总质量为25kg,求: (1)、该机器狗匀加速直线运动时的加速度大小;(2)、从静止开始到最后停止,该机器狗通过的位移;(3)、在减速阶段该机器狗所受合外力。13. 第24届冬奥会将在我国举办。钢架雪车比赛的一段赛道如图1所示,长12m水平直道AB与长20m的倾斜直道BC在B点平滑连接,斜道与水平面的夹角为15°。运动员从A点由静止出发,推着雪车匀加速到B点时速度大小为8m/s,紧接着快速俯卧到车上沿BC匀加速下滑(图2所示),到C点共用时5.0s。若雪车(包括运动员)可视为质点,始终在冰面上运动,其总质量为110kg,sin15°=0.26,求雪车(包括运动员)
(1)、该机器狗匀加速直线运动时的加速度大小;(2)、从静止开始到最后停止,该机器狗通过的位移;(3)、在减速阶段该机器狗所受合外力。13. 第24届冬奥会将在我国举办。钢架雪车比赛的一段赛道如图1所示,长12m水平直道AB与长20m的倾斜直道BC在B点平滑连接,斜道与水平面的夹角为15°。运动员从A点由静止出发,推着雪车匀加速到B点时速度大小为8m/s,紧接着快速俯卧到车上沿BC匀加速下滑(图2所示),到C点共用时5.0s。若雪车(包括运动员)可视为质点,始终在冰面上运动,其总质量为110kg,sin15°=0.26,求雪车(包括运动员) (1)、在直道AB上的加速度大小;(2)、过C点的速度大小;(3)、在斜道BC上运动时受到的阻力大小。14. 图甲是某游乐场的设施图,简化模型如图乙所示。AD、HI为水平轨道,半径m的竖直圆轨道BCB’在最低点稍稍错开,并分别与左右两侧的直轨道平滑相连,轨道BD的长度m;倾斜轨道DE、GH与水平面的夹角θ=53°,长度均为m,和水平轨道平滑相连;水平半圆轨道EFG半径m,和倾斜轨道平滑相连,已知过山车及车上人的总质量kg且可视为质点,过山车从A点运动到B'点时关闭发动机,经过最高点C时对轨道的压力大小为N,过山车沿圆轨道内侧运动一周后沿轨道BDEFGH回到水平轨道HI,最终停在离H点38m处。过山车与直轨道AD、DE、GH的动摩擦因数均为 , 与直轨道HI的动摩擦因数未知,与圆轨道的摩擦均不计,sin53°=0.8,cos53°=0.6,求:
(1)、在直道AB上的加速度大小;(2)、过C点的速度大小;(3)、在斜道BC上运动时受到的阻力大小。14. 图甲是某游乐场的设施图,简化模型如图乙所示。AD、HI为水平轨道,半径m的竖直圆轨道BCB’在最低点稍稍错开,并分别与左右两侧的直轨道平滑相连,轨道BD的长度m;倾斜轨道DE、GH与水平面的夹角θ=53°,长度均为m,和水平轨道平滑相连;水平半圆轨道EFG半径m,和倾斜轨道平滑相连,已知过山车及车上人的总质量kg且可视为质点,过山车从A点运动到B'点时关闭发动机,经过最高点C时对轨道的压力大小为N,过山车沿圆轨道内侧运动一周后沿轨道BDEFGH回到水平轨道HI,最终停在离H点38m处。过山车与直轨道AD、DE、GH的动摩擦因数均为 , 与直轨道HI的动摩擦因数未知,与圆轨道的摩擦均不计,sin53°=0.8,cos53°=0.6,求: (1)、过山车到达C点时的速度大小:(2)、过山车运动到半圆轨道中点F时对轨道的作用力大小;(3)、过山车与直轨道HI的动摩擦因数。15. 如图所示,处于竖直平面内的一探究装置,由倾角=37°的光滑直轨道AB、圆心为O1的半圆形光滑轨道BCD、圆心为O2的半圆形光滑细圆管轨道DEF、倾角也为37°的粗糙直轨道FG组成,B、D和F为轨道间的相切点,弹性板垂直轨道固定在G点(与B点等高),B、O1、D、O2和F点处于同一直线上。已知可视为质点的滑块质量m=0.1kg,轨道BCD和DEF的半径R=0.15m,轨道AB长度 , 滑块与轨道FG间的动摩擦因数 , 滑块与弹性板作用后,以等大速度弹回,sin37°=0.6,cos37°=0.8。滑块开始时均从轨道AB上某点静止释放,
(1)、过山车到达C点时的速度大小:(2)、过山车运动到半圆轨道中点F时对轨道的作用力大小;(3)、过山车与直轨道HI的动摩擦因数。15. 如图所示,处于竖直平面内的一探究装置,由倾角=37°的光滑直轨道AB、圆心为O1的半圆形光滑轨道BCD、圆心为O2的半圆形光滑细圆管轨道DEF、倾角也为37°的粗糙直轨道FG组成,B、D和F为轨道间的相切点,弹性板垂直轨道固定在G点(与B点等高),B、O1、D、O2和F点处于同一直线上。已知可视为质点的滑块质量m=0.1kg,轨道BCD和DEF的半径R=0.15m,轨道AB长度 , 滑块与轨道FG间的动摩擦因数 , 滑块与弹性板作用后,以等大速度弹回,sin37°=0.6,cos37°=0.8。滑块开始时均从轨道AB上某点静止释放, (1)、若释放点距B点的长度l=0.7m,求滑块到最低点C时轨道对其支持力FN的大小;(2)、设释放点距B点的长度为 , 滑块第一次经F点时的速度v与之间的关系式;(3)、若滑块最终静止在轨道FG的中点,求释放点距B点长度的值。16. 如图所示,竖直平面内一倾角的粗糙倾斜直轨道与光滑圆弧轨道相切于点,长度可忽略,且与传送带水平段平滑连接于点。一质量的小滑块从点静止释放,经点最后从点水平滑上传送带。已知点离地高度 , 长 , 滑块与间的动摩擦因数 , 与传送带间的动摩擦因数 , 长度 , 圆弧轨道半径。若滑块可视为质点,不计空气阻力, , , 。求:
(1)、若释放点距B点的长度l=0.7m,求滑块到最低点C时轨道对其支持力FN的大小;(2)、设释放点距B点的长度为 , 滑块第一次经F点时的速度v与之间的关系式;(3)、若滑块最终静止在轨道FG的中点,求释放点距B点长度的值。16. 如图所示,竖直平面内一倾角的粗糙倾斜直轨道与光滑圆弧轨道相切于点,长度可忽略,且与传送带水平段平滑连接于点。一质量的小滑块从点静止释放,经点最后从点水平滑上传送带。已知点离地高度 , 长 , 滑块与间的动摩擦因数 , 与传送带间的动摩擦因数 , 长度 , 圆弧轨道半径。若滑块可视为质点,不计空气阻力, , , 。求: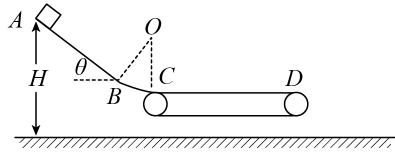 (1)、小滑块经过点时对轨道的压力;(2)、当传送带以顺时针方向的速度转动时,小滑块从水平传送带右端点水平抛出后,落地点到点的水平距离。17. 如图所示,弹射器和竖直圆轨道固定在水平面上,竖直圆轨道在最低点分别与水平轨道BA、BD平滑连接。质量为m=0.1kg的小物块P(可视为质点)从弹射器弹出,经竖直圆轨道后与水平面上的一厚度不计的滑块Q发生弹性碰撞,P经过圆轨道最高点C时轨道对其弹力为F=4N。已知竖直圆轨道的半径r=0.1m,D点左侧轨道光滑,右侧轨道呈粗糙、光滑交替排列,每段的长度均为L=0.1m,Q与粗糙面间的动摩擦因数为μ=0.1,Q的长度也为L=0.1m。P、Q碰撞时间极短,重力加速度g=10m/s²。
(1)、小滑块经过点时对轨道的压力;(2)、当传送带以顺时针方向的速度转动时,小滑块从水平传送带右端点水平抛出后,落地点到点的水平距离。17. 如图所示,弹射器和竖直圆轨道固定在水平面上,竖直圆轨道在最低点分别与水平轨道BA、BD平滑连接。质量为m=0.1kg的小物块P(可视为质点)从弹射器弹出,经竖直圆轨道后与水平面上的一厚度不计的滑块Q发生弹性碰撞,P经过圆轨道最高点C时轨道对其弹力为F=4N。已知竖直圆轨道的半径r=0.1m,D点左侧轨道光滑,右侧轨道呈粗糙、光滑交替排列,每段的长度均为L=0.1m,Q与粗糙面间的动摩擦因数为μ=0.1,Q的长度也为L=0.1m。P、Q碰撞时间极短,重力加速度g=10m/s²。 (1)、求未释放P前弹射器的弹性势能;(2)、要使P与Q碰撞后返回弹射器(返回时被锁定不再弹出),过程中P不脱离圆轨道,求Q的质量M的取值范围;(3)、当M=0.9kg时,Q停在第k个粗糙面上,求k值。
(1)、求未释放P前弹射器的弹性势能;(2)、要使P与Q碰撞后返回弹射器(返回时被锁定不再弹出),过程中P不脱离圆轨道,求Q的质量M的取值范围;(3)、当M=0.9kg时,Q停在第k个粗糙面上,求k值。四、解答题
-
18. 我国在川西山区建成了亚洲最大的风洞群,目前拥有8座世界级风洞设备,具备火箭助推和飞艇带飞等飞行模拟试验能力。如图所示,风洞实验室中可以产生水平向右、大小可调节的风力,现将一套有小球的细直杆放入其中,杆足够长,小球孔径略大于杆直径,其质量为1.1kg,与杆间的动摩擦因数为0.5。当杆与水平方向夹角为37°时,小球沿杆恰好做匀速直线运动,sin37°=0.6,g取10m/s2 , 求此时风力的大小。

-