宁夏中卫市2022届高三理数第一次模拟试卷
试卷更新日期:2022-03-23 类型:高考模拟
一、单选题
-
1. 已知集合 ,则 ( )A、 B、 C、 D、2. 复数 的共轭复数为( )A、 B、 C、 D、3. 已知向量 , 且 , 若 , 均为正数,则的最小值是( )A、24 B、8 C、 D、4. 下列说法错误的是( )A、命题“若则”的逆否命题是“若则” B、命题 , 使得则均有 C、“”是“”的充分不必要条件 D、若为假命题,则均为假命题5. 袋中有红、黄、绿,蓝颜色的球各一个,每次随机取一个后放回袋中,连续取四次,则取出的球颜色完全不相同的概率为( )A、 B、 C、 D、6. 已知在 中,角 的对边分别为 则 边上的高为( )A、1 B、 C、 D、27. “干支纪年法”是我国历法的一种传统纪年法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”;子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥叫做“十二地支”.地支又与十二生肖“鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪”依次对应.“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为甲子、乙丑、丙寅、癸酉:甲戌、乙亥、丙子、…、癸未;甲申、乙寅、丙戌、…、癸已;…;共得到60个组合,称为六十甲子,周而复始,无穷无尽.2020年是“干支纪年法”中的庚子年,那么2082年出生的孩子属相为( )A、猴 B、马 C、羊 D、虎8. 关于函数的图象或性质的说法中,正确的个数为( )
①函数的图象关于直线对称;②将函数的图象向右平移个单位所得图象的函数为;③函数在区间上单调递增;④若 , 则.
A、1 B、2 C、3 D、49. 设函数f(x)=若 , 则实数的取值范围是( )A、 B、 C、 D、10. 已知函数 的两个极值点分别在(-1,0)与(0,1)内,则2a-b的取值范围是( )A、 B、 C、 D、11. 设 分别为双曲线 的左、右焦点,双曲线上存在一点 使得 ,则该双曲线的离心率为( )A、 B、3 C、 D、12. 已知定义域为的函数满足 , 且 , e为自然对数的底数,若关于x的不等式恒成立,则实数a的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 已知是第二象限角,且 , 则.14. 的展开式中, 的系数为.15. 已知抛物线 ,过点 的直线 交 于 , 两点,则直线 ( 为坐标原点)的斜率之积为.16. 在四面体PABC中,平面平面ABC, , , 则该四面体的外接球的体积为.
三、解答题
-
17. 已知数列 的前 项和为 , 且满足 , 设 .(1)、分别求 和 的通项公式;(2)、求数列 的前 项和 .18. 2021年,福建、河北、辽宁、江苏、湖北、湖南、广东、重庆8省市将迎来“3+1+2”新高考模式.“3”指的是:语文、数学、英语,统一高考;“1”指的是:物理和历史,考生从中选一科;“2”指的是:化学、生物、地理和政治,考生从四科中选两科.为了迎接新高考,某中学调查了高一年级1500名学生的选科倾向,随机抽取了100人,统计选考科目人数如下表:
选考物理
选考历史
总计
男生
40
50
女生
总计
30
参考公式: , 其中 .
参考数据:
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
(1)、补全2×2列联表,并根据表中数据判断是否有95%的把握认为“选考物理与性别有关”;(2)、将此样本的频率视为总体的概率,随机调查该校3名学生,设这3人中选考历史的人数为X,求X的分布列及数学期望.19. 如图,在多面体 中,四边形 是边长为2的正方形,四边形 是直角梯形,其中 , ,且 .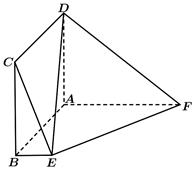 (1)、证明:平面 平面 .(2)、求二面角 的余弦值.20. 如图,椭圆:的一个顶点为 , 离心率为. , 是过点且互相垂直的两条直线,其中,交圆:于 , 两点,交椭圆于另一点.
(1)、证明:平面 平面 .(2)、求二面角 的余弦值.20. 如图,椭圆:的一个顶点为 , 离心率为. , 是过点且互相垂直的两条直线,其中,交圆:于 , 两点,交椭圆于另一点. (1)、求椭圆的方程;(2)、求面积取最大值时直线的方程.
(1)、求椭圆的方程;(2)、求面积取最大值时直线的方程.