湖南省新高考教学教研联盟2022届高三下学期数学3月第一次联考试卷
试卷更新日期:2022-03-23 类型:高考模拟
一、单选题
-
1. 设i是虚数单位,若复数()是纯虚数,则a的值为( )A、1 B、-1 C、2 D、-22. 已知集合 , 集合 , 若 , 则的取值范围是( )A、 B、 C、 D、3. 已知双曲线的一条渐近线为 , 若双曲线的右焦点到的距离是其右顶点到的距离的两倍,则该双曲线的离心率是( )A、 B、2 C、 D、4. 已知随机变量X,Y分别满足,X~B(8,p),Y~N(μ,),且期望E(X)=E(Y),又P(Y≥3)= , 则p=( )A、 B、 C、 D、5. 如图,连接△ABC的各边中点得到一个新的△A1B1C1 , 又连接△A1B1C1各边中点得到一个新的△A2B2C2 , 如此无限继续下去,得到一系列三角形:△ABC,△A1B1C1 , △A2B2C2 , …,这一系列所有三角形的面积和趋向于一个常数.已知A(0,0),B(5,0),C(1,3),则这个常数是( )
 A、 B、5 C、10 D、156. 如图,已知长方体 , 以D为坐标原点, , , 的方向分别为x,y,z轴的正方向建立空间直角坐标系,则 , 又分别是棱 , 的中点,那么三棱锥的体积为( )
A、 B、5 C、10 D、156. 如图,已知长方体 , 以D为坐标原点, , , 的方向分别为x,y,z轴的正方向建立空间直角坐标系,则 , 又分别是棱 , 的中点,那么三棱锥的体积为( )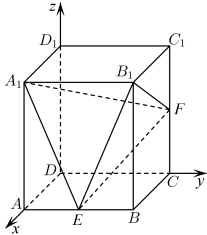 A、4 B、6 C、8 D、127. 函数()的图象向左平移个单位后关于直线对称,则函数在区间上的最小值为( )A、 B、 C、 D、8. 若关于x的不等式的解集是 , 则( )A、 B、 C、 D、
A、4 B、6 C、8 D、127. 函数()的图象向左平移个单位后关于直线对称,则函数在区间上的最小值为( )A、 B、 C、 D、8. 若关于x的不等式的解集是 , 则( )A、 B、 C、 D、二、多选题
-
9. 已知 , 则下列结论正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则的夹角为10. 已知(),则下列结论正确的是( )A、 B、当时,n=5 C、若()的展开式中第7项的二项式系数最大,则n等于12或13 D、当n=4时,11. 已知函数 , 其中为实数,则( )A、函数有两个不同零点0和; B、若对于任意两个不同的实数都有 , 则; C、若在[0,1]上单调递增,则或; D、若有三个不同的实数根,则.12. 如图,E,F,G,H分别是空间四边形ABCD各边上的点(不与各边的端点重合),且AE:EB=AH:HD=m,CF:FB=CG:GD=n,AC⊥BD,AC=4,BD=6.则下列结论正确的是( )
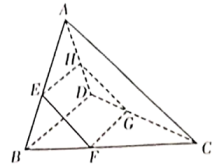 A、E,F,G,H一定共面 B、若直线EF与GH有交点,则交点一定在直线AC上 C、AC∥平面EFGH D、当m=n时,四边形EFGH的面积有最大值6
A、E,F,G,H一定共面 B、若直线EF与GH有交点,则交点一定在直线AC上 C、AC∥平面EFGH D、当m=n时,四边形EFGH的面积有最大值6三、填空题
-
13. .14. 一个盒子里装有除颜色外完全相同的6个小球,盒子中有编号分别为1、2、3、4的红球4个,编号分别为4、5的白球2个,从盒子中任取3个小球(假设取到任何一个小球的可能性相同).则在取出的3个小球中,小球编号最大值为4的概率是.15. 函数(a>0,b>0,a≠1,b≠1)是偶函数,则、与三者间的大小关系是.16. 已知A、B分别是椭圆的左、右顶点,P是椭圆在第一象限内一点,且满足∠PBA=2∠PAB,则.
四、解答题
-
17. 某大型商场为了了解客户对于在其商场销售的某品牌电视机的五种型号的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
某品牌电视机型号
65E3F
65E3G
65E5G
65E7G
65E8G
回访客户(人数)
700
150
200
600
350
满意率
0.5
0.3
0.6
0.3
0.2
满意率是指:某品牌电视机型号的回访客户中,满意人数与总人数的比值假设客户是否满意互相独立,且每种型号电视机客户对于此型号电视机满意的概率与表格中该电视机型号的满意率相等.
(1)、从所有的回访客户中随机抽取1人,求这个客户满意的概率;(2)、从65E3F型号、65E3G型号电视机的所有客户中各随机抽取1人,设其中满意的人数为X,求X的分布列和期望.18. 已知数列的每一项都为正数, , 它的前n项和为 , 且 , , ()成等比数列,(1)、求数列的通项公式;(2)、求并证明:.19. 已知平面四边形.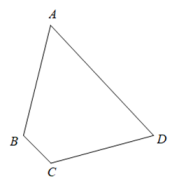 (1)、若 , , 求边的长;(2)、当且时,求.20. 在四棱锥P−ABCD中,平面PAD⊥平面ABCD,O为AD的中点,DC//AB,DC⊥AD,PA=PD,PO=AB=2DC,BC=CD,
(1)、若 , , 求边的长;(2)、当且时,求.20. 在四棱锥P−ABCD中,平面PAD⊥平面ABCD,O为AD的中点,DC//AB,DC⊥AD,PA=PD,PO=AB=2DC,BC=CD,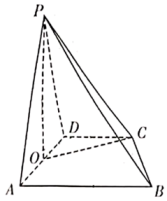 (1)、求证:平面PBC⊥平面POC;(2)、求平面PAB与平面PCB所成角的余弦值.
(1)、求证:平面PBC⊥平面POC;(2)、求平面PAB与平面PCB所成角的余弦值.