浙教版备考2022年中考数学二轮复习训练题11：新定义问题

试卷更新日期：2022-03-23 类型：二轮复习

进入出卷网下载

一、单选题

1. 如 $M = {1 ， 2 ， x}$ ，我们叫集合 $M$ ，其中1，2， $x$ 叫做集合 $M$ 的元素.集合中的元素具有确定性（如 $x$ 必然存在），互异性（如 $x \neq 1$ ， $x \neq 2$ ），无序性（即改变元素的顺序，集合不变）.若集合 $N = {x ， 1 ， 2}$ ，我们说 $M = N$ .已知集合 $A = {1 ， 0 ， a}$ ，集合 $B = {\frac{1}{a} ， | a | ， \frac{b}{a}}$ ，若 $A = B$ ，则 $b - a$ 的值是（）

A、－1 B、0 C、1 D、2

查看试题解析
2. 规定：如果关于x的一元二次方程ax²+bx+c＝0（a≠0）有两个实数根，且其中一个根是另一个根的2倍，则称这样的方程为“倍根方程”现有下列结论
①方程x²+2x﹣8＝0是倍根方程；②若关于x的方程x²+ax+2＝0是倍根方程，则a＝±3；③若（x﹣3）（mx﹣n）＝0是倍根方程，则n＝6m或3n＝2m；④若点（m，n）在反比例函数y＝ $\frac{2}{x}$ 的图象上，则关于x的方程mx²﹣3x+n＝0是倍根方程.上述结论中正确的有（）

A、② B、①③ C、②③④ D、②④

查看试题解析
3. 我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解，并规定：F（n）= $\frac{p}{q}$ .例如：12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所以3×4是12的最佳分解，所以F（12）= $\frac{3}{4}$ .如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t为“吉祥数”.根据以上新定义，下列说法正确的有：（1）F（48）= $\frac{3}{4}$ ；（2）如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数，则对任意一个完全平方数m，总有F（m）=1；（3）15和26是“吉祥数”；（4）“吉祥数”中，F（t）的最大值为 $\frac{3}{4}$ . （）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 新定义：在平面直角坐标系中，对于点 $P (m ， n)$ 和点 $P' (m ， n')$ ，若满足 $m \geq 0$ 时， $n' = n - 4$ ； $m < 0$ 时， $n' = - n$ ，则称点 $P' (m ， n')$ 是点 $P (m ， n)$ 的限变点．例如：点 $P_{1} (2 ， 5)$ 的限变点是 $P_{1}^{'} (2 ， 1)$ ，点 $P_{2} (- 2 ， 3)$ 的限变点是 $P_{2}^{'} (- 2 ， - 3)$ ．若点 $P (m ， n)$ 在二次函数 $y = - x^{2} + 4 x + 2$ 的图象上，则当 $- 1 ≤ m ≤ 3$ 时，其限变点 $P'$ 的纵坐标 $n'$ 的取值范围是（）

A、 $- 2 \leq n' \leq 2$ B、 $1 \leq n' \leq 3$ C、 $1 \leq n' \leq 2$ D、 $- 2 \leq n' \leq 3$

查看试题解析
5. 新定义：在平面直角坐标系中，对于点P（m，n）和点P′（m，n′），若满足m≥0时，n′=n-4；m＜0时，n′=-n，则称点P′（m，n′）是点P（m，n）的限变点．例如：点P₁（2，5）的限变点是P₁′（2，1），点P₂（-2，3）的限变点是P₂′（-2，-3）．若点P（m，n）在二次函数y=-x²+4x+2的图象上，则当-1≤m≤3时，其限变点P′的纵坐标n'的取值范围是（）

A、 $- 2 \leq n^{'} \leq 2$ B、 $1 \leq n^{'} \leq 3$ C、 $1 \leq n^{'} \leq 2$ D、 $- 2 \leq n^{'} \leq 3$

查看试题解析
6. 设 $P (x ， y_{1})$ ， $Q (x ， y_{2})$ 分别是函数 $C_{1}$ ， $C_{2}$ 图象上的点，当 $a \leq x \leq b$ 时，总有 $- 1 \leq y_{1} - y_{2} \leq 1$ 恒成立，则称函数 $C_{1}$ ， $C_{2}$ 在 $a \leq x \leq b$ 上是“逼近函数”， $a \leq x \leq b$ 为“逼近区间”.则下列结论：
①函数 $y = x - 5$ ， $y = 3 x + 2$ 在 $1 \leq x \leq 2$ 上是“逼近函数”；②函数 $y = x - 5$ ， $y = x^{2} - 4 x$ 在 $3 \leq x \leq 4$ 上是“逼近函数”；③ $0 \leq x \leq 1$ 是函数 $y = x^{2} - 1$ ， $y = 2 x^{2} - x$ 的“逼近区间”；④ $2 \leq x \leq 3$ 是函数 $y = x - 5$ ， $y = x^{2} - 4 x$ 的“逼近区间”.其中，正确的有（）

A、②③ B、①④ C、①③ D、②④

查看试题解析
7. 定义：我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图，在正方形 $O A B C$ 中，点 $A (0 ， 2)$ ，点 $C (2 ， 0)$ ，则互异二次函数 $y = {(x - m)}^{2} - m$ 与正方形 $O A B C$ 有交点时 $m$ 的最大值和最小值分别是（）

A、4，-1 B、 $\frac{5 - \sqrt{17}}{2}$ ，-1 C、4，0 D、 $\frac{5 + \sqrt{17}}{2}$ ，-1

查看试题解析
8. 弧三角形，又叫莱洛三角形，是机械字家莱洛首先进行研究的.弧三角形是这样画的：先画正三角形，然后分别以三个顶点为圆心，（晓观数学）其边长为半径画弧得到的三角形.在大片的麦田或农田中，由农作物倒状形成的几何图案被称为“麦田怪圈”.图1中的麦田怪圈主要由圆和弧三角形构成，某研究小组根据照片尝试在操场上绘制类似的图形.如图2，成员甲先借绳子绕行一周画出 $⊙ O$ ，再将 $⊙ O$ 三等分，得到 $A$ ， $B$ ， $C$ 三点.接着，成员乙分别以 $A$ ， $B$ ， $C$ 为圆心画出图中的弧三角形.研究小组在 $A$ ， $B$ ， $C$ ， $O$ 四点中的某一点放置了检测仪器，记成员甲所在的位置为 $P$ ，成员乙所在的位置为 $Q$ ，若将射线 $O B$ 绕着点 $O$ 逆时针旋转到经过甲或乙的旋转角记为自变量 $x$ （单位：°， $0 \leq x < 360$ ），甲、乙两人到检测仪器的距离分别记为 $y_{1}$ 和 $y_{2}$ （单位： $m$ ），绘制出两个函数的图象（如图3）.
结合以上信息判断，下列说法中错误的是（）

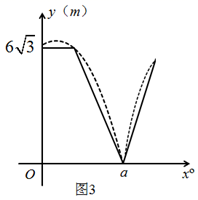A、 $⊙ O$ 的半径为 $6 m$ B、图3中 $a$ 的值为270 C、当 $x = 60$ 时， $y$ ₁取得最大值12 D、检测仪器放置在点 $A$ 处

查看试题解析
9. 数学上有很多著名的猜想，“奇偶归一猜想”就是其中之一，它至今未被证明，但研究发现，对于任意一个小于 $7 \times 1 0^{11}$ 的正整数，如果是奇数，则乘3加1；如果是偶数，则除以2，得到的结果再按照上述规则重复处理，最终总能够得到1．对任意正整数 $m$ ，按照上述规则，恰好实施5次运算结果为1的 $m$ 所有可能取值的个数为（）

A、8 B、6 C、4 D、3

查看试题解析
10. “化积为方”是一个古老的几何学问题，即给定一个长方形，作一个和它面积相等的正方形，这也是证明勾股定理的一种思想方法.如图所示，在矩形 $A B C D$ 中，以 $A D$ 为边做正方形 $A H M D$ ，以 $C D$ 为斜边，作 $R t Δ D C G$ 使得点在 $H M$ 的延长线上，过点 $D$ 作 $D E ⊥ D G$ 交 $A B$ 于 $E$ ，再过 $E$ 点作 $E F ⊥ C G$ 于 $F$ ，连结 $C E$ 交 $M H$ 于 $N$ ，记四边形 $D E N M$ ，四边形 $B C N H$ 的面积分别为 $S_{1} ， S_{2}$ ，若 $S_{1} - S_{2} = 15$ ， $D M = 7$ ，则 $D G$ 为（）

A、8 B、 $2 \sqrt{17}$ C、 $6 \sqrt{2}$ D、 $5 \sqrt{3}$

查看试题解析

二、填空题

11. 定义 $a \otimes b = {\begin{array}{l} a (a - b \leq 1) \\ b (a - b > 1) \end{array}$ ，比如， $4 \otimes 2 = 2$ ， $1 \otimes 5 = 1$ ．若实数 $k$ 满足 $k [x^{2} \otimes (x + 1)] - 1 = 0$ ，并且这个关于 $x$ 的方程有两个不相等的实数解，则 $k$ 的取值范围是．

查看试题解析
12. 我们把直角坐标平面内横、纵坐标互相交换的两个点称为“关联点对”，如点 $A (2 ， 3)$ 和点 $B (3 ， 2)$ 为一对“关联点对”．如果反比例函数 $y = \frac{10}{x}$ 在第一象限内的图像上有一对“关联点对”，且这两个点之间的距离为 $3 \sqrt{2}$ ，那么这对“关联点对”中，距离 $x$ 轴较近的点的坐标为．

查看试题解析
13. 规定：如果一个四边形有一组对边平行，一组邻边相等，那么称此四边形为广义菱形．根据规定判断下面四个结论：①正方形和菱形都是广义菱形；②对角线互相垂直，且两组邻边分别相等的四边形是广义菱形；③一组对边平行，一条对角线平分一个内角的四边形是广义菱形；④若M、N的坐标分别为（0，2），（0， $-$ 2），P是二次函数 $y = \frac{1}{8} x^{2}$ 图象上在第一象限内的任意一点，PQ垂直直线 $y = - 2$ 于点Q ，则四边形PMNQ是广义菱形．其中正确的是．（填序号）

查看试题解析
14. 对于平面直角坐标系xOy中的点P ，给出如下定义：记点P到x轴的距离为d₁ ，到y轴的距离为d₂ ，若d₁≤d₂ ，则称d₁为点P的“引力值”；若d₁＞d₂ ，则称d₂为点P的“引力值”．特别地，若点P在坐标轴上，则点P的“引力值”为0，若点C在直线 $y = - 2 x + 2$ 上，且点C的“引力值”为1，则点C的坐标为．

查看试题解析
15. 定义： $[a ， b ， c]$ 为二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的特征数，下面给出特征数为 $[m ， 1 - m ， 2 - m]$ 的二次函数的一些结论：①当 $m = 1$ 时，函数图象的对称轴是 $y$ 轴；②当 $m = 2$ 时，函数图象过原点；③当 $m > 0$ 时，函数有最小值；④如果 $m < 0$ ，当 $x > \frac{1}{2}$ 时， $y$ 随 $x$ 的增大而减小，其中所有正确结论的序号是．

查看试题解析
16. 我们定义一种新函数：形如y＝|ax²+bx+c|（a≠0，且b²﹣4ac＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y＝|x²﹣2x﹣3|的图像（如图所示），并写出下列结论：
①图像与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；
②图像具有对称性，对称轴是直线x＝1；
③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；
④当x＝﹣1或x＝3时，函数的最小值是0；
⑤当x＝1时，函数的最大值是4；
⑥若点P（a，b）在该图像上，则当b＝2时，可以找到4个不同的点P．其中错误的结论是（填序号）．

查看试题解析

三、综合题

17. 定义：对于一个各数位上的数字都不为0且互不相等的四位正整数，若千位上的数字与个位上的数字之差等于十位上的数字与百位上的数字之和，则称这样的四位数为“匹配数”.将“匹配数”m的千位、百位所组成的两位数与十位、个位所组成的两位数对调，得到一个新的四位数n，记 $F (m) = \frac{m + n}{101}$ .例如，对于6231，各数位上的数字都不为0且互不相等，又因为 $6 - 1 = 2 + 3$ ，所以6231是“匹配数”，
$F (6231) = \frac{6231 + 3162}{101} = 93$ .再如，对于9125，各数位上的数字都不为0且互不相等，但因为 $9 - 5 \neq 1 + 2$ ，所以9125不是“匹配数”.

(1)、判断9432和5213是否为“匹配数”.如果是“匹配数”，请求出 $F (m)$ 的值；如果不是“匹配数”，请说明理由；

(2)、若“匹配数” $m = 9000 + 100 a + 10 b + c$ （ $1 \leq a \leq 9$ ， $1 \leq b \leq 9$ ， $1 \leq c \leq 9$ ，且a，b，c均为整数），且 $F (m)$ 是一个正整数的平方，请求出所有满足条件的m.

查看试题解析
18. 定义：对于函数y=f(x)，若x=a时，y=2a，则称（a，2a）为函数y=f(x)的倍速点；当函数有0个、1个、2个、3个、…、n个、无数个倍速点时，则依次称函数为0阶倍速函数、1阶倍速函数、…、n阶倍速函数、无穷阶倍速函数

(1)、请判断 $y = \frac{2}{x}$ 是否是倍速函数，如果是倍速函数，请直接写出所有倍速点和阶数；

(2)、对于两个不相等的实数a、b，我们规定符号min｛a，b｝表示a、b中较小的值，如min｛2，4｝=2，若函数 $y = (k^{2} - 2) x + k - 2$ 是无穷阶倍速函数，按照符号min｛a，b｝规定解关于x的方程 $m i n {\frac{1}{x - k} ， \frac{3}{x - k}} = \frac{x - 1}{x - k} - k$ ；

(3)、如图，已知正方ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，令 $a = P D - \frac{1}{2} P C$ 的最大值，判断函数 $y = a x^{2} + (a + 2) x + 1$ 是否是倍速函数，如果是倍速函数求出其倍速点和阶数.

查看试题解析
19. 定义：如果两个函数y₁ ， y₂存在x取同一个值，使得y₁＝y₂ ，那么称y₁ ， y₂互为“等值函数”，对应的x值为y₁ ， y₂的“等值根”．

(1)、函数y₁＝ $\frac{1}{2}$ x+b与 $y_{2} = \frac{4}{x}$ 是否互为“等值函数”？如果是，求出当b＝1时，两函数的“等值根”；如果不是，请说明理由．

(2)、如图所示的是y＝﹣|x²+2x|的图象，它是由二次函数y＝﹣x²﹣2x的图象x轴上方的部分沿x轴翻折到x轴下方，图象的其余部分保持不变得到的．若y₁＝ $\frac{1}{2}$ x+b与y₂＝﹣|x²+2x|互为“等值函数”，且有两个“等值根”，求b的取值范围．

查看试题解析
20. 定义；若关于x的一元二次方程ax²+bx+c＝0有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”，若函数G₁的图象与函数G₂的图象相交于A、B两点，其中一个点的横坐标等于另一点的横坐标的2倍，则称函数G₁与函数G₂互为“倍根函数”，A、B两点间的水平距离为“倍宽”.

(1)、若 $(x - 4) (2 x + k) = 0$ 是“倍根方程”，求k的值；

(2)、函数 $y = - m x$ 与 $y = x^{2} - k$ 互为“倍根函数”且“倍宽”为2，求 $m ， k$ 的值；

(3)、直线l：y＝tx+d与抛物线L：y＝2x²+px+q（q≠d）互为“倍根函数”，若直线l与抛物线L相交于A（x₁ ， y₁），B（x₂ ， y₂）两点，且2+2t²≤AB²≤3+3t² ，令6x₀＝|p﹣t|，若二次函数y₀＝﹣（x₀﹣m）²+m²+1有最大值4，求实数m的值.

查看试题解析
21. 定义：如果一个三角形中有两个内角 $α ， β$ 满足 $α + 2 β = 90 °$ ，那我们称这个三角形为“近直角三角形”.

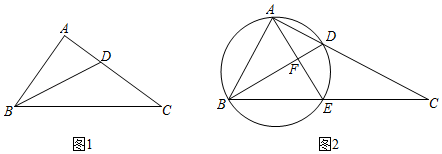(1)、若∆ABC是“近直角三角形”，∠B＞90°，∠C＝50°，则∠A＝度；

(2)、如图1，Rt∆ABC中，∠BAC＝90°，AB＝3，AC＝4．若BD是∠ABC的平分线，
①求证：∆BDC是“近直角三角形”；

②在边AC上是否存在点E（异于点D），使得∆BCE也是“近直角三角形”？若存在，请求出CE的长；若不存在，请说明理由.

(3)、如图2，在Rt∆ABC中，∠BAC＝90°，点D为AC边上一点，以BD为直径的圆交BC于点E，连结AE交BD于点F，若∆BCD为“近直角三角形”，且AB＝5，AF＝3，求tan∠C的值.

查看试题解析
22. 我们定义：有一边相等的两个相似三角形为近等三角形，这两个三角形的面积比为近等比.例如：△ABC的三边分别为9，12，15，△EDF的三边为12，16，20，则易得两个三角形相似，且显然有一边相等，则我们称△ABC与△DEF 近等，或者说△ABC与△DEF为近等三角形，△ABC 与△DEF的近等比为S△ABC： S△DEF.

(1)、如图1，△ABC的顶点在5×5的网格图中格点上，AD为BC边上的高，则图中与是其中一对近第三角形，它们的近等比为.

(2)、如图2，△ABC是内接于圆О的等腰直角三角形，BC为斜边，BD平分∠ABC，点D在圆上，BD交AC于点E，找出图中任意一组近等三角形，并求出它们的近等比.

(3)、如图3，△ABC中，∠BAC=30°，AB=2，过线段AB的圆分别交线段BC，AC于D、E两点，连结AD，DE，当△ABD一边与CD相等且与△CDE是一对近等三角形时，求△ADE的面积.

查看试题解析
23. 新定义：在一个四边形中，若有一组对角都等于90°，则称这个四边形为双直角四边形.如图1，在四边形ABCD中，∠A＝∠C＝90°，那么四边形ABCD就是双直角四边形.

(1)、若四边形ABCD是双直角四边形，且AB＝3，BC＝4，CD＝2，求AD的长；

(2)、已知，在图2中，四边形ABCD内接与⊙O，BC＝CD且∠BAC＝45°；
①求证：四边形ABCD是双直角四边形；
②若AB＝AC，AD＝1，求AB的长和四边形ABCD的面积.

查看试题解析
24. 定义：若两个三角形有一对公共边，且另有一组对应边和一对对应角分别对应相等，那么这两个三角形称为邻等三角形.
例如：如图1，△ABC中，AD＝AD，AB＝AC，∠B＝∠C，则△ABD与△ACD是邻等三角形.

(1)、如图2，⊙O中，点D是 $\overset{⌢}{B C}$ 的中点，那么请判断△ABD与△ACD是否为邻等三角形，并说明理由.

(2)、如图3，以点A（2，2）为圆心，OA为半径的⊙A交x轴于点B（4，0），△OBC是⊙A的内接三角形，∠COB＝30°.
①求∠C的度数和OC的长；
②点P在⊙A上，若△OCP与△OBC是邻等三角形时，请直接写出点P的坐标.

查看试题解析