北师大版备考2022中考数学二轮复习专题4 二次根式
试卷更新日期:2022-03-23 类型:二轮复习
一、单选题(共30分)
-
1. 已知 , 则的平方根是( )A、2 B、-2 C、±2 D、±12. 已知a= ,b= ,则a与b的关系是( )A、相等 B、互为相反数 C、互为倒数 D、平方值相等3. 下列运算正确的有( )A、5ab﹣ab=4 B、3 ﹣ =3 C、a6÷a3=a3 D、 + =4. 若等腰三角形的两边长分别为 和 ,则这个三角形的周长为( )
A、 B、 或 C、 D、5. 已知x为实数,化简 的结果为( )A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 若 ,则 的值为: ( )
A、0 B、1 C、-1 D、28. 等式 成立的条件是( )
A、x≠3 B、x≥0 C、x≥0且x≠3 D、x>39. 已知:m, n是两个连续自然数(m<n),且q=mn, 设 , 则p( )。A、总是奇数 B、总是偶数 C、有时奇数,有时偶数 D、有时有理数,有时无理数10. 对于任意的正数m、n定义运算※为:m※n= , 计算(3※2)×(8※12)的结果为( )A、2﹣4 B、2 C、2 D、20二、填空题(共27分)
-
11. 记的整数部分是 , 小数部分是 , 则的值为.12. 若 有意义,则x的取值范围是.13. 计算( +1)2015( ﹣1)2014=
14. 已知x1= + ,x2= ﹣ ,则x12+x22= .
15. 若x、y都为实数,且 ,则 =。16.若
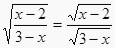 成立,则x满足17. 如图,已知 , ,第四象限的点 到 轴的距离为 ,若 , 满足 ,则 点坐标为; 与 轴的交点坐标为.
成立,则x满足17. 如图,已知 , ,第四象限的点 到 轴的距离为 ,若 , 满足 ,则 点坐标为; 与 轴的交点坐标为. 18. 观察下列等式:
18. 观察下列等式:① ;
②
③
…
参照上面等式计算方法计算:
.
三、解答题(共63分)
-
19. 若x , y为实数,且y= + + .求 - 的值.20. 已知 的三边长为 , , ,化简 .21. 计算(1)、(2)、已知 .求代数式 的值.(3)、先化简,再求值 ,其中m=(4)、解分式方程: +3.22. 阅读下面材料,回答问题:(1)、在化简 的过程中,小张和小李的化简结果不同;
小张的化简如下: = = =
小李的化简如下: = = =
请判断谁的化简结果是正确的,谁的化简结果是错误的,并说明理由.
(2)、请你利用上面所学的方法化简:① ;② .23. 阅读下列材料,然后回答问题,在进行二次根式的化简与运算时,我们有时会碰上如如 一样的式子,其实我们还可以将其进一步化简:= = (1)
以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:
= (2)
(1)、请参照(1)(2)的方法用两种方法化简:方法一: =
方法二: =
(2)、直接写出化简结果: = =(3)、计算: + + +…+ +24. 如图,平面直角坐标系中,已知 , 且a、b满足.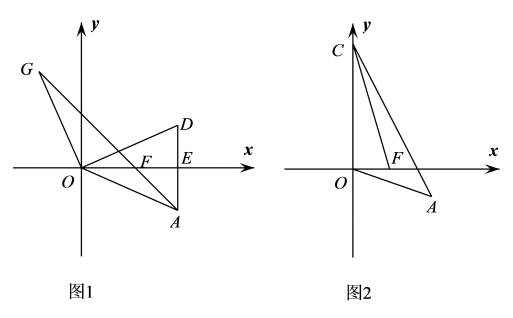 (1)、求A点的坐标;(2)、如图1,已知点F(1,0),点A、D关于x轴对称,连接AD交x轴于E,OG⊥OD交AF的延长线于G,求AF:GF的值;(3)、如图2若点F(1,0)、C(0,3),连AC、FC,试确定∠ACO+∠FCO的值是否发生变化?若不变,说明理由;若变化,请求出变化范围.
(1)、求A点的坐标;(2)、如图1,已知点F(1,0),点A、D关于x轴对称,连接AD交x轴于E,OG⊥OD交AF的延长线于G,求AF:GF的值;(3)、如图2若点F(1,0)、C(0,3),连AC、FC,试确定∠ACO+∠FCO的值是否发生变化?若不变,说明理由;若变化,请求出变化范围.